СПОСОБ: Разложение левой части уравнения на множители

1. СПОСОБ: Разложение левой части уравнения на множители.

Решим уравнение

х² + 10х - 24 = 0.

Разложим левую часть на множители:

х² + 10х - 24 = х² + 12х - 2х - 24 = х(х + 12) - 2(х + 12) = (х + 12)(х - 2).

Следовательно, уравнение можно переписать так:

(х + 12)(х - 2) = 0

Так как произведение равно нулю, то, по крайней мере, один из его множителей равен нулю. Поэтому левая часть уравнения обращается нуль при х = 2, а также при х = - 12. Это означает, что число 2 и - 12 являются корнями уравнения х² + 10х - 24 = 0.

2. СПОСОБ: Метод выделения полного квадрата.

Решим уравнение х² + 6х - 7 = 0.

Выделим в левой части полный квадрат.

Для этого запишем выражение х² + 6х в следующем виде:

 

х² + 6х = х² + 2• х • 3.

В полученном выражении первое слагаемое - квадрат числа х, а второе - удвоенное произведение х на 3. По этому чтобы получить полный квадрат, нужно прибавить 3², так как

х² + 2• х • 3 + 3² = (х + 3)².

Преобразуем теперь левую часть уравнения

х² + 6х - 7 = 0,

прибавляя к ней и вычитая 3². Имеем:

х² + 6х - 7 = х² + 2• х • 3 + 3² - 3² - 7 = (х + 3)² - 9 - 7 = (х + 3)² - 16.

Таким образом, данное уравнение можно записать так:

(х + 3)² - 16 =0, (х + 3)² = 16.

Следовательно, х + 3 - 4 = 0, х₁ = 1, или х + 3 = -4, х₂ = -7.

 

3. СПОСОБ: Решение квадратных уравнений по формуле.

Умножим обе части уравнения

ах² + bх + с = 0, а ≠ 0

на 4а и последовательно имеем:

4а²х² + 4аbх + 4ас = 0,

((2ах)² + 2ах • b + b²) - b² + 4ac = 0,

(2ax + b)² = b² - 4ac,

2ax + b = ± √ b² - 4ac,

2ax = - b ± √ b² - 4ac,

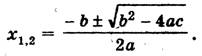
Примеры.

а) Решим уравнение: 4х² + 7х + 3 = 0.

а = 4, b = 7, с = 3, D = b² - 4ac = 7² - 4 • 4 • 3 = 49 - 48 = 1,

D > 0, два разных корня;

 

Таким образом, в случае положительного дискриминанта, т.е. при

b² - 4ac >0 , уравнение ах² + bх + с = 0 имеет два различных корня.

 

б) Решим уравнение: 4х² - 4х + 1 = 0,

а = 4, b = - 4, с = 1, D = b² - 4ac = (-4)² - 4 • 4 • 1= 16 - 16 = 0,

 D = 0, один корень;

Итак, если дискриминант равен нулю, т.е. b² - 4ac = 0, то уравнение

ах² + bх + с = 0 имеет единственный корень,

 

в) Решим уравнение: 2х² + 3х + 4 = 0,

а = 2, b = 3, с = 4, D = b² - 4ac = 3² - 4 • 2 • 4 = 9 - 32 = - 13 , D < 0.

Данное уравнение корней не имеет.

Итак, если дискриминант отрицателен, т.е. b² - 4ac < 0,

уравнение ах² + bх + с = 0 не имеет корней.

Формула (1) корней квадратного уравнения ах² + bх + с = 0 позволяет найти корни любого квадратного уравнения (если они есть), в том числе приведенного и неполного. Словесно формула (1) выражается так: корни квадратного уравнения равны дроби, числитель которой равен второму коэффициенту, взятому с противоположным знаком, плюс минус корень квадратный из квадрата этого коэффициента без учетверенного произведения первого коэффициента на свободный член, а знаменатель есть удвоенный первый коэффициент.

 

4. СПОСОБ: Решение уравнений с использованием теоремы Виета.

Как известно, приведенное квадратное уравнение имеет вид

 

х² + px + c = 0. (1)

Его корни удовлетворяют теореме Виета, которая при а =1 имеет вид

x₁ x₂ = q,

 x₁ +x₂ = - p

Отсюда можно сделать следующие выводы (по коэффициентам p и q можно предсказать знаки корней).

 а) Если сводный член q приведенного уравнения (1) положителен (q > 0), то уравнение имеет два одинаковых по знаку корня и это зависти от второго коэффициента p. Если р < 0, то оба корня отрицательны, если р < 0, то оба корня положительны.

Например,

x² – 3x + 2 = 0; x₁ = 2 и x₂ = 1, так как q = 2 > 0 и p = - 3 < 0;

x² + 8x + 7 = 0; x₁ = - 7 и x₂ = - 1, так как q = 7 > 0 и p= 8 > 0.

б) Если свободный член q приведенного уравнения (1) отрицателен (q < 0), то уравнение имеет два различных по знаку корня, причем больший по модулю корень будет положителен, если p < 0 , или отрицателен, если p > 0 .

Например,

x² + 4x – 5 = 0; x₁ = - 5 и x₂ = 1, так как q= - 5 < 0 и p = 4 > 0;

x² – 8x – 9 = 0; x₁ = 9 и x₂ = - 1, так как q = - 9 < 0 и p = - 8 < 0.