Навигация
Квадратные уравнения и уравнения высших порядков
Министерство образования Российской Федерации
Муниципальное общеобразовательное учреждение
"Средняя общеобразовательная школа №22"
Квадратные уравнения и уравнения высших порядков
Выполнили:
Ученики 8 "Б" класса
Кузнецов Евгений и Руди Алексей
Руководитель:
Зенина Алевтина Дмитриевна
преподаватель математики
Тюмень
2005
Оглавление
Введение
Глава 1. История квадратных уравнений и уравнений высших порядков
1.1 Уравнения в Древнем Вавилоне
1.2 Уравнения арабов
1.3 Уравнения в Индии
Глава 2. Теория квадратные уравнения и уравнения высших порядков
2.1 Основные понятия
2.2 Формулы четного коэффициента при х
2.3 Теорема Виета
2.4 Квадратные уравнения частного характера
2.5 Теорема Виета для многочленов (уравнений) высших степеней
2.6 Уравнения, сводимые к квадратным (биквадратные)
2.7 Исследование биквадратных уравнений
2.8 Формулы Кордано
2.9 Симметричные уравнения третьей степени
2.10 Возвратные уравнения
2.11 Схема ГорнераЗаключение
Список используемой литературы
Приложение 1
Приложение 2
Приложение 3
Введение
Уравнения в школьном курсе алгебры занимают ведущее место. На их изучение отводится времени больше, чем на любую другую тему. Действительно, уравнения не только имеют важное теоретическое значение, но и служат чисто практическим целям. Подавляющее число задач о пространственных формах и количественных отношениях реального мира сводится к решению различных видов уравнений. Овладевая способами их решения, мы находим ответы на различные вопросы из науки и техники (транспорт, сельское хозяйство, промышленность, связь и т. д.).
В этом реферате хотелось бы отобразить формулы и способы решения различных уравнений. Для этого приводятся уравнения, которые не изучаются в школьной программе. В основном это уравнения частного характера и уравнения высших степеней. Чтобы раскрыть эту тему приводятся доказательства этих формул.
Задачи нашего реферата:
- улучшить навыки решения уравнений
- наработать новые способы решения уравнений
- выучить некоторые новые способы и формулы для решения этих уравнений.
Объект исследования - элементарная алгебра Предмет исследования уравнения. Выбор этой темы основывался на том, что уравнения есть как в программе начальной, так и в каждом последующем классе общеобразовательных школ, лицеев, колледжей. Многие геометрические задачи, задачи по физике, химии и биологии решаются с помощью уравнений. Уравнения решали двадцать пять веков назад. Они создаются и сегодня – как для использования в учебном процессе, так и для конкурсных экзаменов в вузы, для олимпиад самого высокого уровня.
Глава 1. История квадратных уравнений и уравнений высших порядков
1.1 Уравнения в Древнем Вавилоне
Алгебра возникла в связи с решением разнообразных задач при помощи уравнений. Обычно в задачах требуется найти одну или несколько неизвестных, зная при этом результаты некоторых действий, произведённых над искомыми и данными величинами. Такие задачи сводятся к решению одного или системы нескольких уравнений, к нахождению искомых с помощью алгебраических действий над данными величинами. В алгебре изучается общие свойства действий над величинами.
Некоторые алгебраические приемы решения линейных и квадратных уравнений были известны еще 4000 лет назад в Древнем Вавилоне. Необходимость решать уравнения не только первой, но и второй степени еще в древности была вызвана потребностью решать задачи, связанные с нахождением площадей земельных участков и с земельными работами военного характера, а также с развитием астрономии и самой математики. Как было сказано ранее, квадратные уравнения умели решать около 2000 лет до нашей эры вавилонянами. Применяя современную алгебраическую запись, можно сказать, что в их клинописных текстах встречаются как неполные, так и полные квадратные уравнения.
Правило решения этих уравнений, изложенное в вавилонских текстах, совпадает по существу с современными, однако неизвестно, каким образом дошли вавилоняне до этого правила. Почти все найденные до сих пор клинописные тексты приводят только задачи с решением, изложенными в виде рецептов, без указаний относительно того, каким образом они были найдены.
Несмотря на высокий уровень развития алгебры в Вавилоне, в клинописных текстах отсутствует понятие отрицательного числа и общие методы решения квадратного уравнения.
1.2 Уравнения арабов
Некоторые способы решения уравнений как квадратных, так и уравнений высших степеней были выведены арабами. Так известный арабский математик Ал-Хорезми в своей книге «Ал - джабар» описал многие способы решения различных уравнений. Их особенность была в том, что Ал-Хорезми применял сложные радикалы для нахождения корней (решений) уравнений. Необходимость в решении таких уравнений была нужна в вопросах о разделе наследства.
Похожие работы
... f ¢(xо) = 0, >0 (<0), то точка xоявляется точкой локального минимума (максимума) функции f(x). Если же =0, то нужно либо пользоваться первым достаточным условием, либо привлекать высшие производные. На отрезке [a,b] функция y = f(x) может достигать наименьшего или наибольшего значения либо в критических точках, либо на концах отрезка [a,b]. Пример 3.22. Найти экстремумы функции f(x) ...
... список или выбрать из 2-3 текстов наиболее интересные места. Таким образом, мы рассмотрели общие положения по созданию и проведению элективных курсов, которые будут учтены при разработке элективного курса по алгебре для 9 класса «Квадратные уравнения и неравенства с параметром». Глава II. Методика проведения элективного курса «Квадратные уравнения и неравенства с параметром» 1.1. Общие ...
... решения от численных методов расчёта. Для определения корней уравнения не требуется знания теорий групп Абеля, Галуа, Ли и пр. и применения специальной математической терминологии: колец, полей, идеалов, изоморфизмов и т.д. Для решения алгебраического уравнения n - ой степени нужно только умение решать квадратные уравнения и извлекать корни из комплексного числа. Корни могут быть определены с ...
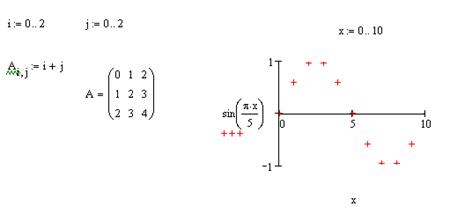
... с единицами измерений физических величин в системе MathCAD? 11. Подробно охарактеризуйте текстовые, графические и математические блоки. Лекция №2. Задачи линейной алгебры и решение дифференциальных уравнений в среде MathCAD В задачах линейной алгебры практически всегда возникает необходимость выполнять различные операции с матрицами. Панель операторов с матрицами находится на панели Math. ...


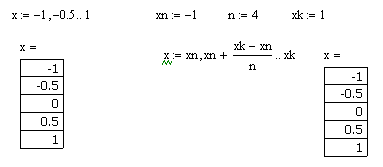
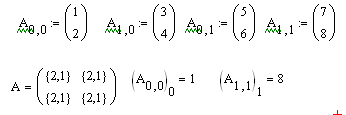

0 комментариев