Оценка точности по разностям двойных измерений и по невязкам в полигонах и ходах

3.5 Оценка точности по разностям двойных измерений и по невязкам в полигонах и ходах.

В практике геодезических работ часто одну и ту же величину измеряют дважды. Например, стороны теодолитного хода в прямом и обратном направлении, углы двумя полуприемами, превышения – по черной и красной стороне вех. Чем точнее произведены измерения, тем лучше сходимость результатов в каждой паре.

m_lср. = ½ √∑d²/n

где d – разности в каждой паре; n – количество разностей.

Формула Бесселя:

m_lср = ½ √∑d²/n-1

Если измерения должны удовлетворять какому-либо геометрическому условию, например, сумма внутренних углов треугольника должна быть 180˚, то точность измерений можно определить по невязкам получающимся в результате погрешностей измерений.

μ=√∑ [f² /n]/N,

где - СКП одного угла;

f – невязка в полигоне;

N – количество полигонов;

n – количество углов в полигоне.

4. Определение дополнительных пунктов

4.1 Цель и методы определения дополнительных пунктов

Дополнительные пункты определяются наряду со съемочной сетью в основном для сгущения существующей геодезической сети пунктами съемочного обоснования. Они строятся прямыми, обратными, комбинированными, а при наличии электронных дальномеров – линейными засечками и лучевым методом.

В некоторых случаях дополнительный пункт определяется передачей (снесением) координат с вершины знака на землю.

4.2 Передача координат с вершины знака на землю. (Решение примера)

При производстве топографо-геодезических работ в городских условиях невозможно бывает установить теодолит на пункте геодезической сети (пунктом является церковь, антенна и т.п.). Тогда и возникает задача по снесению координат пункта триангуляции на землю для обеспечения производства геодезических работ на данной территории.

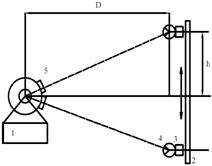
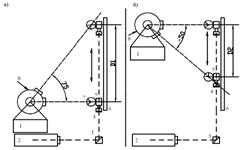
Исходные данные: пункт A с координатами X_A, Y_A; пункты геодезической сети B (X_B, Y_B) и C (X_C, Y_C).

Полевые измерения: линейные измерения выбранных базисов b₁ и b'₁; измерения горизонтальных углов ß₁ , ß'₁ , ß₂ , ß'₂ ; б , б'.

Требуется найти координаты точки P – X_P, Y_P.

Решение задачи разделяется на следующие этапы:

Решение числового примера

Исходные данные

Вычисление расстояния D_АР

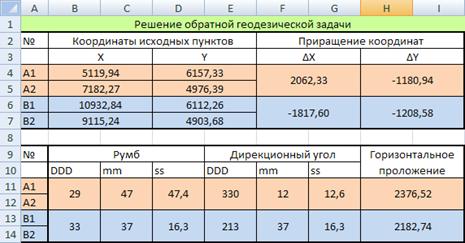
Решение обратных задач

Вычисление дирекционных углов α_{АР =} α_D

sin ψ = D×sinб/ S _AB; sin =174,52×0,66179/3068,48=0,03950;

sin ψ' = D×sinб'/ S _AС; sin `=174,52×0,95061/5275,51=0,03292;

ψ = arcsin 0,03950 =2 ^o15` 50``;

ψ'= arcsin 0,03292=1 ^o53` 13``;

φ = 180 ^o – (б+ ψ) = 180 ^o – (138^o33` 49``+2 <sup>o</sup>15` 50``) = 39<sup>o</sup>10` 41``

φ`= 180 <sup>o</sup> – (б`+ ψ` ) = 180 <sup>o</sup> – (71<sup>o</sup>55` 02``+1 <sup>o</sup>53` 13``) = 106 ^o11` 46``

α_D =α_AB ± φ =329^o07` 55``+ 39<sup>o</sup>10` 41``= 8<sup>o</sup>18` 36``

α_D`=α<sub>AC</sub> ± φ`=262^o07` 51``+ 106 <sup>o</sup>11` 46``= 8<sup>o</sup>18` 37``

Контроль:

(α_D–α'_D) õm_β;

где m_β –СКП измерения горизонтальных углов.

Знак «+» или «-» в формулах вычисления дирекционного угла берется в зависимости от взаимного расположения пунктов А, Р, В и С.

(8^o18` 36``-8<sup>o</sup>18` 37``) ≤ 30``

0^o00` 01`` ≤ 30``

Решение прямых задач (вычисление координат т.Р)

Х_p = Х_А+∆Х,Y_p = Y_А+∆Y,

Х'_p = Х_А+∆Х',Y'_p = Y_А+∆Y'.

∆Х= Dcosα_D,∆Y= Dsinα_D,

∆Х'= Dcosα'_D,∆Y'=Dsinα'_D.

Расхождение координат не должно превышать величины õm_ß×p, где p=206265", m_ß – средняя квадратическая погрешность измерения угла.

Оценка точности определения положения пункта P.

Средняя квадратическая погрешность определения отдельного пункта вычисляется по формуле:

M²_p = m²_X +m²_Y,M²_p = m²_D +(D×m_α / P)²

где m_D- определяется точностью линейных измерений, а m_α – точностью угловых измерений.

Пример: m_D =2см, m_α= 5``, тогда

M_p =√ [(0,02) ²+(170×5/2×10⁵)²] ≈ 2×10^-2 = 0,02м.

Похожие работы

Использование современной компьютерной техники и программного обеспечения для решения прикладных задач в области геодезических измерений

Скачать

45197

6

28

- уравнивание геодезических сетей, Mapsuite - создание инженерно-топографических планов, LEICA Geo Office - обработка геодезических измерений, SiteMaster - автоматизация обмерных работ, GeometricalGeodesy - решение геодезических задач в системе Mathematica, предназначены для решения различных геодезических задач. В данной работе представлено решение аналогичных задач с помощью языка ...

Первоначальная обработка геодезических измерений

Скачать

28905

0

0

... них не окажется нужной, то тогда средство необходимо разработать вручную, если это оправдано с точки зрения затраченного времени и материальных ресурсов. 2. Обработка геодезических измерений с использованием электронных таблиц Для первоначальной обработки информации, полученной в результате комплекса топографо-геодезических работ, мною использовалась программа “ТОГИ”, являющаяся пакетом ...

Геодезические работы

Скачать

63691

0

17

... на стройплощадке необходимо соблюдение требований норм и правил по технике безопасности, изложенных в главе СНиП Ш-4-80 "Техника безопасности в строительстве" и ведомственных инструкциях. К выполнению геодезических работ допускаются лица, прошедшие инструктаж, оформленный приказом по строительному управлению. Опасность получения травмы или увечья определяется в зависимости от условий рабочего ...

Разработка методов и средств поверки и калибровки геодезических приборов для измерения превышений

Скачать

36487

2

12

... -электронных приборов при непосредственном участии автора. Вторая глава. Во второй главе рассмотрены разработанные методы проведения исследований метрологических установок и стендов для поверки и калибровки геодезических приборов для измерения превышений. Метод исследования короткопериодической погрешности измерения вертикальных углов геодезических приборов. Важной задачей при исследовании ...