Геодезические сети сгущения
Системы координат WGS-84 и СК-95
Измерения в геодезических сетях
Устройство электронного тахеометра. Измерение им горизонтальных и вертикальных углов, расстояний, координат Х, У, Н точек местности
Классификация погрешностей геодезических измерений. Средняя квадратическая погрешность. Формы Гаусса и Бесселя для её вычисления
Веса измерений
Оценка точности по разностям двойных измерений и по невязкам в полигонах и ходах
Решение прямой и обратной засечки (по варианту задания)
Уравнивание системы ходов съемочной сети
Тахеометрическая съёмка
Нанесение съёмочных и реечных точек
Навигация
Решение прямой и обратной засечки (по варианту задания)
Основы геодезических измерений
88097
знаков
19
таблиц
0
изображений
4.3 Решение прямой и обратной засечки (по варианту задания)
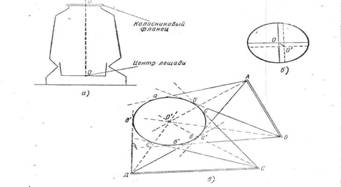
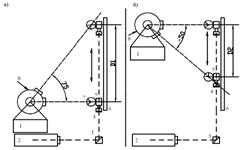
Определение координат пункта прямой засечкой (формулы Юнга).
Для однократной засечки необходимо иметь два твёрдых пункта. Контроль определения осуществляется вторичной засечкой с третьего твёрдого пункта.
Исходные данные: твердые пункты А(ХАYА); B(ХBYB); С(ХСYС).
Полевые измерения: горизонтальные углы β1, β 2, β`1, β`2.
Определяется пункт P.
Формулы для решения задачи:
Хp -ХА=((ХB-ХА) ctg β 1+(YB-YА))/ (ctg β 1+ ctg β 2);
Хp= ХА+∆ХА;
Yp -YА=((YB-YА) ctg β 1+(ХB-ХА))/ (ctg β 1+ ctg β 2); Yp= YА+∆YА;
Оценка точности определения пункта P.
Вычисление СКП из 1-го и 2-го определения:
M1 =(mβ×√(S12+ S22))/p×sinγ1;
M2 =(mβ×√(S12+ S22))/p×sinγ2;
Значения величин, входящих в приведённые формулы следующие:
mβ =5``, p=206265``; γ=73˚15,9`; γ=62˚55,7`; S1=1686,77 м; S2=1639,80 м; S3=2096,62 м.
Стороны засечки найдены из решения обратных задач.
M1 = (5``×√2,86+2,69)/(2×105×0,958)=0,06м.
M2 = (5``×√2,69+4,41)/(2×105×0,890)=0,07м.
Mr = √ (M12 +M22); Mr =√ [(0,06) 2+(0,07) 2]=0,09м.
Расхождение между координатами из двух определений
r = √ [( Хp- Х`p) 2+( Yp- Y`p) 2] не должно превышать величины 3 Mr;
r =√ [(2833,82-2833,82) 2+(2116,38-2116,32) 2]=√0,0036=0,06м.
На основании неравенства r =0,06м 3×0,09м логично сделать вывод о качественном определении пункта P.
За окончательные значения координат принимают среднее из двух определений.
Решение числового примера
| β1 β2 | XB XA | ctg β1 ctg β2 (XB- XA)ctg β1 | YB YA | ∆ XA XP = XA+∆XA | (YB-YA)ctgβ1 | ∆ YA YP=YA+∆YA | |||
| XB- XA | YB-YA | ||||||||
| ctg β1 + ctg β2 | |||||||||
| 52˚16.7' 52˚27.4' | 1630.16 1380.25 | 0.77349
193.30 1.48792 | 3230.00 1260.50 | 1453.57 2833.82 | 1523.39 | 855.88 2116.38 | |||
| +249.91 | +1969.50 | ||||||||
| β'1 β'2 | XC XB | ctg β'1 ctg β'2 (XC- XB)ctg β'1 | YC YB | ∆ XB XP = XA+∆XA | (YC-YB)ctgβ'1 | ∆ YB YP=YA+∆YA | |||
| XC- XB | YC-YB | ||||||||
| ctg β'1 + ctg β'2 | |||||||||
| 69˚48.5' 52˚27.4' | 3401.04 1630.16 | 0.36777 0.92402
1.29175 | 4133.41 3230.00 | 1203.56 2833.82 | 332.24 | -1113.68 2116.32 | |||
| +1770.88 | +903.41 | ||||||||
| |||||||||
0.71443
651.282833.82 2116.35
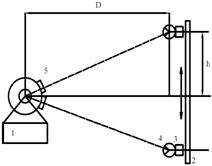
Определение координат пункта методом обратной засечки (аналитическое решение задачи Потенота).
Необходимо иметь три твёрдых пункта, для решения задачи с контролем используют четвёртый твердый пункт.
Исходные данные: А(ХАYА); B(ХBYB); С(ХСYС), D(XDYD).
Полевые измерения: горизонтальные углы γ1, γ2, γ3.
Определяемый пункт P.
Формулы для вычисления:
1.ctgγ1=а; ctgγ2=b
2.k1 =a(YB- YA)-( ХB- ХA);
3.k2 =a( ХB- ХA)+(YB- YA);
4.k3 =b(YС- YA)-( ХC- ХA);
5.k4 =b( ХC- ХA)-(YC- YA);
6.c=( k2 - k4)/( k1 - k3)=ctgaAP;
7.контроль: k2 - с k1= k1- с k3;
8.∆Y=( k2 - с k1)/( 1 - с2);
9.∆Х= с AY;
10.Хp = ХА+∆Х, Yp = YА+∆Y.
Решение численного примера
| 1 | γ1 γ2 a=ctg γ1 b=ctg γ2 | 109˚48'42" 224˚15'21" -0.360252 +1.026320 |
| 2 | XB XC XA | 5653.41 8143.61 6393.71 |
| X'B = XB- XA X'C = XC- XA | -740.30 1749.90 | |
| X'C- X'B = XC- XB | 2490.20 | |
| YB YC YA | 1264.09 1277.59 3624.69 | |
| Y'B = YB- YA Y'C = YC- YA | -2360.60 -2347.16 | |
| Y'C- Y'B = YC- YB | 13.5 | |
| 3 | k1 k3 | +1590.71 -4158.78 |
| k1- k3 | +5749.49 | |
| k2 k4 | -2093.91 -551.14 | |
| k2- k4 | -1542.77 | |
| c = ctg α c2 + 1 k2-ck1 k4-ck3 | -0.268332 1.072002 -1667.07 -1667.07 | |
| 4 | ∆Y YA Y ∆X XA X | -1555.0 3624.65 +2069.56 +417.28 6393.71 +6810.99 |
Координаты из первого определения получились Хp=6810,99м, Yp =2069,56 м.
Для контроля задача решается вторично с твердым пунктом D, т.е. пунктом А, B, C.
Исходными данными являются: γ1=109o48`42``; γ3=151o26`24``; Хd=6524,81м, Yd=893,64м.
Контроль осуществляется следующим образом: определить
ctgαPD =( ХD-ХP)/( YD-YP), αPD=256o27`38``;
Из схемы первого решения имеем: С=ctgαPA=-0,26833;
αPD=105o01`13``.
Контроль определяется пунктом P:
r=√ [( ХP - Х`P) 2+( YP - Y`P) 2] ≤ 3 Mr;
где r, как и в случае прямой засечки,
Mr=1/2×√ [M12 +M22]
Похожие работы
- уравнивание геодезических сетей, Mapsuite - создание инженерно-топографических планов, LEICA Geo Office - обработка геодезических измерений, SiteMaster - автоматизация обмерных работ, GeometricalGeodesy - решение геодезических задач в системе Mathematica, предназначены для решения различных геодезических задач. В данной работе представлено решение аналогичных задач с помощью языка ...
... них не окажется нужной, то тогда средство необходимо разработать вручную, если это оправдано с точки зрения затраченного времени и материальных ресурсов. 2. Обработка геодезических измерений с использованием электронных таблиц Для первоначальной обработки информации, полученной в результате комплекса топографо-геодезических работ, мною использовалась программа “ТОГИ”, являющаяся пакетом ...
... на стройплощадке необходимо соблюдение требований норм и правил по технике безопасности, изложенных в главе СНиП Ш-4-80 "Техника безопасности в строительстве" и ведомственных инструкциях. К выполнению геодезических работ допускаются лица, прошедшие инструктаж, оформленный приказом по строительному управлению. Опасность получения травмы или увечья определяется в зависимости от условий рабочего ...
... -электронных приборов при непосредственном участии автора. Вторая глава. Во второй главе рассмотрены разработанные методы проведения исследований метрологических установок и стендов для поверки и калибровки геодезических приборов для измерения превышений. Метод исследования короткопериодической погрешности измерения вертикальных углов геодезических приборов. Важной задачей при исследовании ...
0 комментариев