Навигация
Формулы связи координат точек местности и координат их изображений на стереопаре снимков идеального случая съемки
2. Формулы связи координат точек местности и координат их изображений на стереопаре снимков идеального случая съемки
В идеальном случае съемки угловые элементы ориентирования снимков стереопары w1=a1=À1=w2=a2=À2=0, а базис фотографирования параллелен оси Х системы координат объекта OXYZ.
В этом случае координаты базиса ![]() будут равны BX=B, BY=BZ=O (B-модуль
будут равны BX=B, BY=BZ=O (B-модуль ![]() ).
).
Примем, что ![]() , то есть начало системы координат объекта OXYZ совмещено с точкой S1), f1=f2=f, a x0i=y0i=0.
, то есть начало системы координат объекта OXYZ совмещено с точкой S1), f1=f2=f, a x0i=y0i=0.
Так как угловые элементы ориентирования снимков равны нулю, то
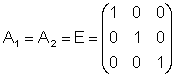 ,
,
а 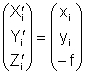 ,
,
где i – номер снимка.
При этом выражение (1 .13) примет вид
![]() , (1)
, (1)
а выражение (1 .4), которое мы представим в виде
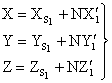
будет иметь вид
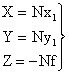 , (2)
, (2)
а с учетом ( 1)
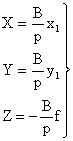 . (3)
. (3)
Так как из третьего уравнения выражения (3) следует, что
![]() ,
,
то формулы связи координат (3) можно представить в виде
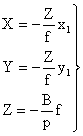 (4)
(4)
3. Определение координат точек местности по стереопаре снимков методом двойной обратной фотограмметрической засечки
Для определения координат точек местности по стереопаре снимков методом прямой фотограмметрической засечки необходимо, чтобы были известны элементы внешнего ориентирования снимков. В большинстве случаев практики их значения не известны. В этом случае определение координат точек местности по стереопаре снимков выполняют методом двойной обратной фотограмметрической засечки.
Решение задачи по этому методу выполняется в следующей последовательности:
1. Определяют элементы взаимного ориентирования снимков. Пять элементов взаимного ориентирования снимков определяют взаимную угловую ориентацию стереопары снимков и базиса фотографирования. Для их определения необходимо измерить не менее пяти соответственных точек на стереопаре снимков;
2. Строят фотограмметрическую модель объекта по измеренным на стереопаре снимков координатам изображений соответственных точек и значениям элементов взаимного ориентирования снимков. Построенная модель подобна сфотографированному объекту, но имеет произвольный масштаб и произвольно расположена и ориентирована относительно системы координат объекта;
3. Определяют элементы внешнего ориентирования фотограмметрической модели по опорным точкам. Эти семь элементов определяют масштаб модели, ее положение и ориентацию относительно системы координат объекта. Для их определения достаточно трех опорных точек, не лежащих на одной прямой. По значениям элементов внешнего ориентирования фотограмметрической модели и элементов взаимного ориентирования можно определить элементы внешнего ориентирования стереопары снимков;
4. По координатам точек, определенных в системе координат модели, и элементам внешнего ориентирования модели определяют координаты точек в системе координат объекта.
4. Условие, уравнения и элементы взаимного ориентирования снимков
На рис. 1 представлена стереопара снимков Р1 и Р2 в положении, которое они занимали в момент фотографирования.
Любая пара соответственных лучей в этом случае пересекается в точке М местности и лежит в плоскости, проходящей через базис фотографирования ![]() (базисной плоскости).
(базисной плоскости).
Очевидно, что в этом случае векторы ![]() , лежащие в базисной плоскости, компланарны.
, лежащие в базисной плоскости, компланарны.
 |
Рис. 1
Как известно из аналитической геометрии, смешанное произведение компланарных векторов равно нулю.
![]() . ( .1)
. ( .1)
Условие компланарности в координатной форме имеет вид:
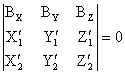 . ( 2)
. ( 2)
В уравнении ( 2) ![]() координаты векторов
координаты векторов ![]() в системе координат фотограмметрической модели ОМХМYMZM, в общем случае произвольно расположенной и ориентированной.
в системе координат фотограмметрической модели ОМХМYMZM, в общем случае произвольно расположенной и ориентированной.
В дальнейшем эту систему координат будем называть просто системой координат модели.
Условие ( 2) связывает между собой только направления векторов и выполняется при любых значениях их модулей. Поэтому значение модуля вектора ![]() можно выбрать произвольно. Направление вектора
можно выбрать произвольно. Направление вектора ![]() определяется двумя независимыми величинами. В качестве этих величин можно выбрать координаты bz и bу вектора
определяется двумя независимыми величинами. В качестве этих величин можно выбрать координаты bz и bу вектора ![]() , коллинеарного вектору
, коллинеарного вектору ![]() , задав величину координаты bx произвольно.
, задав величину координаты bx произвольно.
В частном случае величину bx можно выбрать равной 1.
При этом направление вектора ![]() будут определять величины:
будут определять величины:
![]() и
и ![]() .
.
Выражение (2) в этом случае будет иметь вид:
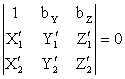 ( 3)
( 3)
В уравнении (3)
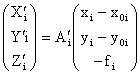 ,
,
где i – номер снимка, а А’1 – ортогональная матрица, элементы aij которой являются функциями угловых элементов ориентирования i-го снимка wi’,ai’,Ài’ относительно системы координат модели ОМХМYMZM.
В выражении (3), которое является уравнением взаимного ориентирования в общем виде, куда кроме координат соответственных точек, измеренных на стереопаре снимков, и элементов внутреннего ориентирования входят 8 параметров by, bz, w1’, a1’, À1’, w2’, a2’, À2’, которые определяют угловую ориентацию базиса фотографирования и стереопары снимков относительно системы координат модели ОМХМYMZM.
Причем параметры w1’ и w2’ определяют поворот снимков стерепары вокруг оси ХМ, параметры bz, a1’, a2‘ – поворот базиса фотографирования и стереопары снимков вокруг оси YM, а параметры by, À1’, À2 ‘– поворот базиса фотографирования и стереопары снимков вокруг оси ZM.
Однако, из этих 8 параметров только 5 определяют взаимную угловую ориентацию базиса фотографирования и стереопары снимков.
Условие (3) выполняется при любой ориентации системы координат модели ОМХМYMZM. Следовательно, ее можно ориентировать таким образом, чтобы 3 из 8 параметров стали равны нулю.
Очевидно, что в общем случае можно сделать равным нулю только один из параметров, входящих в три группы параметров:
– w1’, w2’;
– bz, a1’, a2‘;
– by, À1’, À2’.
–
Таким образом, в качестве элементов взаимного ориентирования можно выбрать любую комбинацию из восьми параметров by, bz, w1’, a1’, À1’, w2’, a2’, À2’, кроме комбинаций, в которые одновременно входят две тройки параметров bz, a1’, a2‘ и by, À1’, À2’, а также пара параметров w1’ и w2’.
Рассмотрим наиболее распространенные системы элементов взаимного ориентирования:
Система a1’, À1’, w2’, a2’, À2’. Если принять при этом, что by=bz= w1’=0, то уравнение (3) имеет вид:
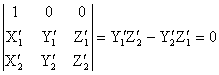 . ( 4)
. ( 4)
Система by, bz, w2’, a2’, À2’. Если при этом принять, что w1’= a1’= À1’ =0, то уравнение (3) будет иметь вид:
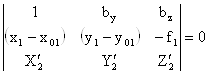 ; ( 5)
; ( 5)
так как 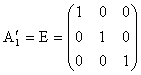 .
.
Комментарий. 3 оставшихся из 8 параметров после выбора 5 элементов взаимного ориентирования задают ориентацию системы координат модели ОМХМYMZM. Например, выбрав систему элементов взаимного ориентирования by, bz, w2’, a2’, À2’ и приняв, что w1’= a1’= À1’ =0, мы таким образом задаем систему координат модели ОМХМYMZM, которой параллельны осям x, y, z системы координат первого снимка стереопары S1x1y1z1. В общем случае значения трех параметров можно задавать произвольно.
Похожие работы
... мест с точностью до нескольких сантиметров. Недостатком метода являются высокая стоимость электронных емкостных влагомеров. Влагомер МГ-4 предназначен для оперативного производственного контроля влажности строительных материалов и изделий, пилопродукции и деревянных деталей по ГОСТ 21718 и ГОСТ 16588. Влагомер может быть использован для измерения влажности широкой номенклатуры твёрдых и сыпучих ...
... большую часть ученых сто лет назад, сегодня трещит по всем швам, не выдерживая потока новых открытий, а также существования других теорий происхождения человека, которые мы рассмотрим ниже. Теория эволюции человека А. Харди Не противоречит теории эволюции, а только слегка заменяет нашего прародителя теория ученного А.Харди, который считает, что человек произошел от водной обезьяны. Главное ...
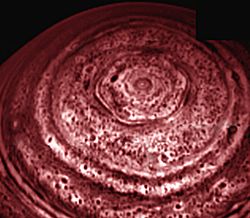
... грозовые разряды, полярные сияния, ультрафиолетовое излучение водорода. 2.1. «ГИГАНТСКИЙ ГЕКСАГОН» Гигантский гексагон — на сегодняшний день не имеющий строгого объяснения атмосферный феномен на планете Сатурн. Представляет собой геометрически правильный шестиугольник с поперечником в 25 тыс. километров, находящийся на северном полюсе Сатурна. По всей видимости, гексагон является ...
... бытовых проблем Коэффициенты: K1 – воображение, мечты K2 – психологическое влияние K3 – физическое состояние организма K4 – эмоциональное состояние организма K5 – время общения Как вы понимаете, я не первый, кто разработал свою формулу любви. Люди давно пытаются определить закономерности развития любви и описать механизмы ее возникновения с помощью аналитических законов и формул. Но мои ...




0 комментариев