Навигация
Внешнее ориентирование модели. Элементы внешнего ориентирования модели
7. Внешнее ориентирование модели. Элементы внешнего ориентирования модели
 |
Рис. 1
На рис.1: OXYZ - система координат объекта, ОМХМYMZM - система координат фотограмметрической модели , А – точка объекта ,АМ -точка фотограмметрической модели, соответствующая точке А объекта .
Векторы ![]() определяют положение начала системы координат модели ОМХМYMZM и точки А местности относительно начала системы координат объекта OXYZ.
определяют положение начала системы координат модели ОМХМYMZM и точки А местности относительно начала системы координат объекта OXYZ.
Векторы ![]() определяют соответственно положение точек АМ и А относительно системы координат фотограмметрической модели.
определяют соответственно положение точек АМ и А относительно системы координат фотограмметрической модели.
Из рис. 1 следует, что
![]()
![]() . ( 1)
. ( 1)
Векторы ![]() коллинеарны, поэтому
коллинеарны, поэтому
![]() ; ( 2)
; ( 2)
где t – знаменатель масштаба модели.
С учетом ( 2) выражение ( 1) имеет вид:
![]() ; ( .3)
; ( .3)
В координатной форме выражение ( 3) имеет вид:
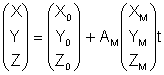 ; ( 4)
; ( 4)
Или
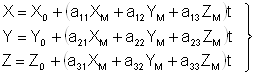 . ( .5)
. ( .5)
В выражениях ( 4) и ( 5):
X, Y, Z – координаты точки объекта в системе координат объекта;
ХМ,YM,ZM - координаты соответствующей точки модели в системе координат фотограмметрической модели;
АМ – матрица преобразования координат, элементы aij которой являются функциями углов wМ, aМ, ÀМ, определяющих ориентацию системы координат модели относительно системы координат объекта;
t – знаменатель масштаба модели.
7 параметров: ![]() - называют элементами внешнего ориентирования модели.
- называют элементами внешнего ориентирования модели.
8. Определение элементов внешнего ориентирования модели по опорным точкам
Для определения элементов внешнего ориентирования модели по опорным точкам в качестве исходных используют уравнения ( 7.5), которые представим в виде:
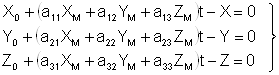 . ( 1)
. ( 1)
Каждая планово-высотная опорная точка (X,Y,Z) позволяет составить 3 уравнения ( 1), в которых неизвестными являются 7 элементов внешнего ориентирования модели. Каждая плановая опорная точка (X,Y) позволяет составить два первых уравнения из выражения ( 1), а каждая высотная опорная точка (Z) – третье уравнение из выражения ( 1).
Для определения элементов внешнего ориентирования модели необходимо составить систему не менее чем из 7 уравнений. Очевидно, что для этого необходимо иметь не менее двух планово-высотных и одной высотной опорной точки. Задачу можно также решить, если иметь две плановые и три высотные опорные точки.
Так как уравнения ( 1) не линейны, их приводят к линейному виду и переходят к уравнениям поправок.
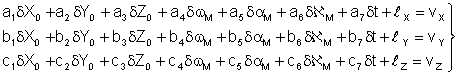 . ( 2)
. ( 2)
В уравнении поправок:
ai, bi, ci – частные производные от уравнений ( 1) по соответствующим переменным ;
ℓX, ℓY, ℓZ– свободные члены.
Значения коэффициентов уравнений поправок ai, bi, ci вычисляют по известным значениям координат ХМ,YM,ZM и X, Y, Z и приближенным значениям неизвестных. Значения свободных членов ℓX, ℓY, ℓZвычисляют таким же образом по формулам ( .1).
Полученную таким образом систему уравнений поправок решают методом последовательных приближений. Если количество уравнений поправок в системе больше семи, то ее решают по методу наименьших квадратов (под условием VTPV=min).
9. Определение элементов внешнего ориентирования снимков стереопары
По элементам внешнего ориентирования модели и элементам взаимного ориентирования можно определить элементы внешнего ориентирования снимков стереопары.
Линейные элементы внешнего ориентирования снимков ![]() определяют по формулам:
определяют по формулам:
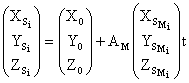 ; ( 1)
; ( 1)
в которых ![]() - координаты центра проекции i-го снимка стереопары в системе координат модели.
- координаты центра проекции i-го снимка стереопары в системе координат модели.
Угловые элементы внешнего ориентирования снимков wi, ai, Ài определяют в следующей последовательности:
1. Сначала получают матрицу преобразования координат i-го снимка
![]() ; ( 2)
; ( 2)
АМ – матрица, в которой элементы aij вычисляют по угловым элементам внешнего ориентирования модели wМ, aМ, ÀМ ;
Ai’ – матрица, в которой элементы aij вычисляют по угловым элементам взаимного ориентирования i-го снимка wi’, ai’, Ài’.
2. Затем по элементам aij матрицы Ai вычисляют угловые элементы внешнего ориентирования i-го снимка стереопары:
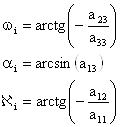 .
.
10. Точность определения координат точек объекта по стереопаре снимков
Для предрасчета точности определения координат точек местности по стереопаре аэрофотоснимков, учитывая, что углы наклона снимков не превышают 1°- 3°, а базис фотографирования практически горизонтален, воспользуемся формулами связи координат точек местности и координат их изображений на стереопаре снимков идеального случая съемки ( 2.4):
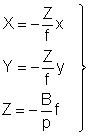 . ( 2.4)
. ( 2.4)
Сначала получим среднюю квадратическую ошибку определения высоты точки Z местности. Для этого продифференцируем третью формулу выражения (1.8.4) по аргументу р.
![]() .
.
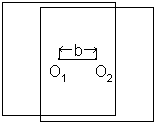 |
Заменим величину р на b – базис в масштабе снимка.
Рис.1
На рис.1 О1и О2 – главные точки снимка.
В результате получим
![]() .
.
Перейдя к средним квадратическим ошибкам получим формулу:
![]() . ( 1)
. ( 1)
Для получения средних квадратических ошибок определения координат Х и Y точки местности продифференцируем первые две формулы выражения (1.8.4) по аргументам x, y, Z и перейдем к средним квадратическим ошибкам.
В результате получим
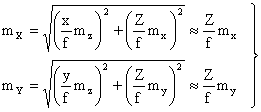 . ( 2)
. ( 2)
В качестве примера вычислим величины mX, mY и mZ точек местности, определенных по стереопаре снимков масштаба 1:5000, полученной АФА с f =150 мм и форматом кадра 23х23 см, с продольным перекрытием 60%.
Будем считать, что на стереопаре снимков точки были измерены с ошибками
![]() .
.
В этом случае высота фотографирования
![]() ;
;
а базис фотографирования в масштабе снимка
![]() .
.
Средние квадратические ошибки определения координат точки местности, вычисленные по формулам ( 1) и ( 2) будут равны:
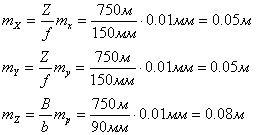 .
.
Похожие работы
... мест с точностью до нескольких сантиметров. Недостатком метода являются высокая стоимость электронных емкостных влагомеров. Влагомер МГ-4 предназначен для оперативного производственного контроля влажности строительных материалов и изделий, пилопродукции и деревянных деталей по ГОСТ 21718 и ГОСТ 16588. Влагомер может быть использован для измерения влажности широкой номенклатуры твёрдых и сыпучих ...
... большую часть ученых сто лет назад, сегодня трещит по всем швам, не выдерживая потока новых открытий, а также существования других теорий происхождения человека, которые мы рассмотрим ниже. Теория эволюции человека А. Харди Не противоречит теории эволюции, а только слегка заменяет нашего прародителя теория ученного А.Харди, который считает, что человек произошел от водной обезьяны. Главное ...
... грозовые разряды, полярные сияния, ультрафиолетовое излучение водорода. 2.1. «ГИГАНТСКИЙ ГЕКСАГОН» Гигантский гексагон — на сегодняшний день не имеющий строгого объяснения атмосферный феномен на планете Сатурн. Представляет собой геометрически правильный шестиугольник с поперечником в 25 тыс. километров, находящийся на северном полюсе Сатурна. По всей видимости, гексагон является ...
... бытовых проблем Коэффициенты: K1 – воображение, мечты K2 – психологическое влияние K3 – физическое состояние организма K4 – эмоциональное состояние организма K5 – время общения Как вы понимаете, я не первый, кто разработал свою формулу любви. Люди давно пытаются определить закономерности развития любви и описать механизмы ее возникновения с помощью аналитических законов и формул. Но мои ...




0 комментариев