Навигация
Лінійна модель виробництва
15556
знаков
1
таблица
2
изображения
ЛІНІЙНА МОДЕЛЬ ВИРОБНИЦТВА
1. Лінійні моделі виробництва та лінійне програмування
Будь-яке національне господарство розвивається в складній мережі міжгалузевих взаємозв'язків, які зрозуміти шляхом простого математичного апарату неможливо. Наприклад, попит на автомобілі впливає не тільки на автомобільну промисловість, але непрямо і на металургію – виробника базової сировини для виготовлення автомобілів, і на галузі, пов'язані з виробництвом шин, і інших комплектуючих частин, а також на галузі, які виготовляють радіоелектронне устаткування та ін. Прості розрахунки показують, що «лобовий» підхід та арифметика не допоможуть при спробі кількісного аналізу прямого й непрямого ефекту поширення таких впливів.
Метод міжгалузевого аналізу, розроблений американським економістом російського походження Василем Леонтьєвим, дозволяє дати послідовні та чисельно впевнені відповіді на запитання, пов'язані з міжгалузевими взаємодіями й їх впливами на основні макроекономічні показники.
Розглянемо діяльність найнижчої ланки макроекономіки (виробничої одиниці – заводу, цеху). Потрібно скласти план виробництва, який забезпечує максимальний ступень виконання завдання. Щодо даної виробничої одиниці відомі її технічні можливості, а також кількість сировинних ресурсів, які можна використати.
Нехай кількість всіх видів ресурсів 
позначимо їх 
. Це можуть бути метал, електроенергія, різні види поставок з інших підприємств. Припустимо, що на виробництві можуть випускатися 
типів товарів 
.
Технологією виробництва товарів 
назвемо набір чисел 
, що показують, яка кількість ресурсів 
необхідні для випуску однієї одиниці товару 
. Так виробництво товарів 
можна подати як конвеєр, протягом якого подаються ресурси в кількості 
а в кінці конвеєра виходить готова одиниця продукту .
Отже, можна скласти технологічну матрицю, яка повністю описує технологічні можливості виробництва. Позначаємо її через 
.
Нехай задані кількості 
ресурсів ,, які можуть бути використані у виробництві, тоді 
– вектор ресурсів. Назвемо планом виробництва вектор 
, що показує, яка кількість товарів буде вироблена.
Вважатимемо технологію виробництва лінійною, тобто припустимо, що всі витрати ресурсів зростають прямо пропорційно обсягу випуску. Припустимо, що витрати під час випуску 
одиниць продукту описуються вектором 
, причому одночасне функціонування декількох технологічних процесів приводить до сумарних витрат.
Отже, витрати ресурсів, необхідні для виконання плану виробництва , описуються вектором, координати якого мають такий вигляд:
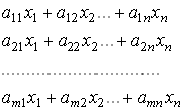
або в матричній формі вектором 
. Умова обмеженості ресурсів записується у вигляді 
. Отже, при заданому векторі ресурсів розглянутою виробничою одиницею може бути будь-який випущений набір товарів 
, який задовольняє обмеженням 
, 
. Як правило, такий вектор не єдиний. У зв'язку з цим з'являється можливість вибору найкращого в деякому розумінні плану.
Розглянемо можливі постановки оптимізаційної задачі. Нехай задані ціни 
на продукти виробництва 
. Потрібно визначити план виробництва, що максимізує вартість продукції. Формальний запис цієї задачі такий:
, , .(1)
Така постановка задачі відповідає принципу планування за валом. Випадок, коли планування випуску проводиться за номенклатурою товарів, можна змоделювати інакше. Нехай заданий вектор 
, що визначає один комплект випуску. Потрібно випустити як можна більше таких комплектів. Нехай 
означає кількість комплектів, що випускають. Розглянемо задачу
, , 
, .(2)
Тут нерівність означає, що вектор містить не менше повних комплектів продукції, що випускається.
Моделі (1), (2), хоча й відбивають певні риси реального виробництва, є, значно ідеалізованими. Так, відсутнє таке важливе для виробництва поняття, як час. Вважається, що всі необхідні ресурси , доступні. Отже, такі моделі абстраговані від динаміки виробництва й не враховують цілий ряд інших показників, які є неодмінним атрибутом реального виробництва.
Незважаючи на розходження змістовних результатів ілюстративні лінійні моделі (1), (2) мають багато спільного, а саме є стандартними задачами лінійного програмування. Основними обчислювальними схемами розв’язування задач лінійного програмування є симплекс-метод і його модифікації.
Похожие работы
... й головним економічним ресурсом, що забезпечує економічне зростання і подальший розвиток. Тому в основі нової моделі економічного зростання лежать інвестиції в людський та інтелектуальний капітал, в економіку знань. Ці зусилля повинні бути підкріплені формуванням національної інноваційної системи, інформаційної економіки, сектора високих технологій. Значна роль при цьому відводиться державі. Саме ...
... малих об’ємів встановлюється на постійному рівні. З формули (1.7) легко отримати вираз для цього граничного значення: Висновки. В даній дипломній роботі була побудована імітаційна модель взаємодії підприємства з ринком, що дозволяє прогнозувати обсяги вироництва в будь-який момент в майбутньому. Проаналізувавши отриману модель, можна стверджувати, що прогнози отримані при ...
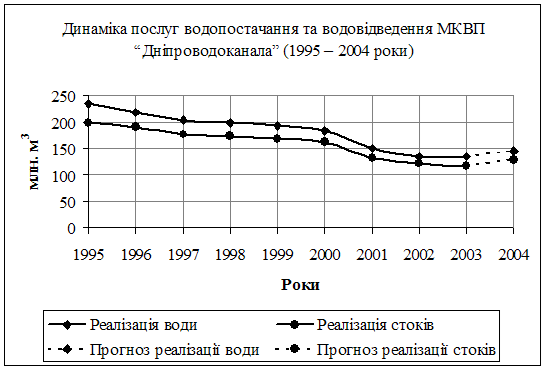
... "Баланс" за 2007 – 2008 роки (додаток В); - форма № 2 "Звіт про фінансові результати" за 2007 – 2008 роки (додаток Г). 3 Підвищення ефективності виробництва МКВП "Дніпроводоканал" на підставі методів Економіко-математичного моделювання У грудні 2008 року Дніпропетровський міськвиконком та комунальне Підприємство "Дніпроводоканал", яке знаходиться у власності м. Дніпропетровська ...
... ринок. Водночас, населення продовжує нарощувати заощадження у банківській системі, надаючи перевагу гривневим вкладенням, та будувати житло. [8] 2. Державна інноваційна політика 2.1. Державне регулювання інноваційної діяльності в Україні Державне регулювання інноваційної діяльності в Україні здійснюється відповідно до Постанови Верховної Ради України "Про концепцію науково-технологі ...
0 комментариев