Навигация
Зв'язок між коефіцієнтами прямих і повних витрат
15556
знаков
1
таблица
2
изображения
5. Зв'язок між коефіцієнтами прямих і повних витрат
Нехай розглядається матриця коефіцієнтів прямих витрат у натуральному або вартісному виразі 
.
Для виробництва одиниці продукції 
-ї галузі необхідно затратити набір продуктів 
, що описується -м стовпцем матриці 
. Але для виробництва цього набору 
необхідно безпосередньо затратити набір продуктів, який ми позначимо через 
.
Елементи вектора витрат називаються коефіцієнтами непрямих витрат першого порядку відповідних продуктів на виробництво одиниць -го продукту 
.
Матриця 
, складена зі стовпців , 
, називається матрицею непрямих витрат першого порядку й визначається відповідно до формули
.
Непрямими витратами другого порядку називають прямі витрати, необхідні для забезпечення непрямих витрат першого порядку, тобто 
, або в матричній формі
де 
– матриця коефіцієнтів непрямих витрат другого порядку.
Продовжуючи за аналогією, назвемо непрямими витратами порядку 
прямі витрати на забезпечення непрямих витрат порядку 
. Очевидно, що матрицю коефіцієнтів непрямих витрат -го порядку одержимо, помноживши 
на 
. (9)
Визначимо тепер повні витрати як суму прямих і непрямих витрат усіх порядків. Відповідно до цього матриця 
, складена з коефіцієнтів повних витрат, утвориться як сума
(10)
або з огляду на те, що 
, маємо
(11)
Коефіцієнти прямих і повних матеріальних витрат мають важливе значення для характеристики структури техніко-економічних зв'язків і для аналізу ефективності виробництва з боку витрат упредметненої праці. Суттєва відмінність коефіцієнтів повних витрат від коефіцієнтів прямих витрат полягає в тому, що вони є не галузевими, а народногосподарськими показниками й формуються з урахуванням технологічних зв'язків між галузями.
З'ясуємо такий момент. Чи не виявляться будь-які з коефіцієнтів повних витрат нескінченно великими?
Розглянемо матрицю 
.
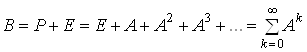Очевидно, що елементи матриці скінченні разом з елементами матриці 
тільки в тому випадку, якщо скінченна сума ряду 
. Крім того, відповідно до умови (3) його збіжність є умовою, еквівалентною продуктивності матриці , причому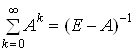 
. Отже, у випадку продуктивності матриці й тільки в цьому випадку матриця повних витрат скінченна, її визначають відповідно до формули
.
Для великих значень 
важко обчислити зворотну матрицю. В цьому випадку матрицю , як і матрицю , можна обчислити приблизно, користуючись методом ітерацій. На першій ітерації 
, на другій ітерації 
, на третій 
, на 
-й ітерації 
. Часткова сума 
відрізняється від часткової суми 
на величину 
. Через те що ряд збігається, 
при 
. Тому за скінченну кількість кроків можна досягти заданої точності обчислень.
Коефіцієнти 
матриці 
мають таку економічну інтерпретацію: якщо випуск кінцевого -го продукту потрібно збільшити на одиницю, то валовий випуск 
-го продукту має бути збільшений на .
6. Коефіцієнти трудових витрат. Баланс трудових ресурсів
Модель Леонтьєва, як відзначалося раніше, відображає лише потенційні можливості, закладені в технології виробничого сектора. У даній моделі передбачається, що процес виробництва відбувається миттєво – всі проміжні продукти вважаються виробленими до того моменту, коли в них з'являється потреба, тобто кожна галузь здатна зробити будь-який обсяг своєї продукції за умови, що їй буде забезпечена сировина в необхідній кількості. Насправді, це не так, оскільки виробничі можливості будь-якої галузі обмежені наявним обсягом основних фондів трудових ресурсів.
Розглянемо проблему розподілу трудових ресурсів, яку можна дослідити за допомогою моделі Леонтьєва.
Зіставимо кожній -ї галузі число 
, що виражає необхідні витрати трудових ресурсів при одиничній інтенсивності даного технологічного процесу.
Нехай 
– вектор прямих витрат праці й – матриця прямих матеріальних витрат. На виробництво одиниці продукту виду необхідно безпосередньо затратити набір продуктів 
і працю в кількості 
. Однак на виробництво даного набору продуктів у свою чергу необхідно затратити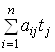 
одиниць праці. Ця величина називається непрямими витратами праці першого порядку на одиницю -го продукту й позначається через 
.
Вектор непрямих витрат праці першого порядку 
визначається таким виразом: 
.
Міркуючи аналогічно тому, як це робилося під час побудови коефіцієнтів непрямих матеріальних витрат, дійдемо висновку, що вектор 
непрямих витрат праці порядку 
визначається таким співвідношенням:
або 
.
Повні витрати праці 
є сумою прямих і непрямих витрат праці
.
У матричному записі, вважаючи, що 
і, з огляду на те, що 
, маємо
або 
.
Якщо матриця продуктивна, то суму в дужках можна замінити на 
й, отже, 
– матриця повних витрат праці.
Зменшення повних витрат праці на одиницю продукції є узагальнюючим показником збільшення продуктивності праці, ефективності виробництва. Розрахунок коефіцієнтів повних витрат праці важливий для ціноутворення на етапі встановлення об'єктивної основи ціни – вартості. Для обчислення коефіцієнтів повних витрат праці використовують ітераційну процедуру
,
що дозволяє з заданою точністю визначити дані коефіцієнти.
Похожие работы
... й головним економічним ресурсом, що забезпечує економічне зростання і подальший розвиток. Тому в основі нової моделі економічного зростання лежать інвестиції в людський та інтелектуальний капітал, в економіку знань. Ці зусилля повинні бути підкріплені формуванням національної інноваційної системи, інформаційної економіки, сектора високих технологій. Значна роль при цьому відводиться державі. Саме ...
... малих об’ємів встановлюється на постійному рівні. З формули (1.7) легко отримати вираз для цього граничного значення: Висновки. В даній дипломній роботі була побудована імітаційна модель взаємодії підприємства з ринком, що дозволяє прогнозувати обсяги вироництва в будь-який момент в майбутньому. Проаналізувавши отриману модель, можна стверджувати, що прогнози отримані при ...
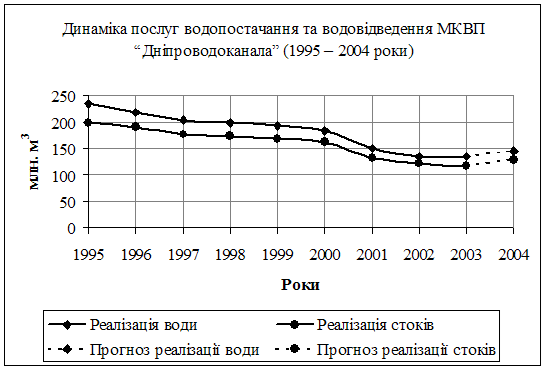
... "Баланс" за 2007 – 2008 роки (додаток В); - форма № 2 "Звіт про фінансові результати" за 2007 – 2008 роки (додаток Г). 3 Підвищення ефективності виробництва МКВП "Дніпроводоканал" на підставі методів Економіко-математичного моделювання У грудні 2008 року Дніпропетровський міськвиконком та комунальне Підприємство "Дніпроводоканал", яке знаходиться у власності м. Дніпропетровська ...
... ринок. Водночас, населення продовжує нарощувати заощадження у банківській системі, надаючи перевагу гривневим вкладенням, та будувати житло. [8] 2. Державна інноваційна політика 2.1. Державне регулювання інноваційної діяльності в Україні Державне регулювання інноваційної діяльності в Україні здійснюється відповідно до Постанови Верховної Ради України "Про концепцію науково-технологі ...
0 комментариев