Визначимо передатні функції розімкненої та замкненої САК відносно вхідної

3.2  Визначимо передатні функції розімкненої та замкненої САК відносно вхідної

а) передатну функцію розімкненої САК визначимо як добуток передатних функцій усіх ланцюгів САК, оскільки маємо послідовне з’єднання ланцюгів. Таким чином

w(s)=w_ир(s)·w_ун(s)·w_ум(s)·w_ид(s)·w_р(s) =,

w(s) = .

Схема розімкненої САК зображена на рис. 3.

б) передатну функцію замкненої САК отримаємо за формулою

Ф(s) = :

Ф(s) = .

Зображення схеми замкненої САК зображена на рис. 4.

3.3 Визначимо стійкість системи по критерію Гурвіца

Знаючи перехідну функцію, знайдемо характеристичне рівняння системи:

D(s)=.

На основі отриманих коефіцієнтів характеристичного рівняння побудуємо головний визначник Гурвіца:

D = .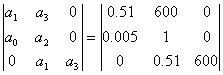

За критерієм Гурвіца для того, щоб система автоматичного керування була стійкою, необхідно та достатньо, щоб при а₀>0 всі визначники Гурвіца були додатними. Умовою стійкості для системи третього порядку будуть: а₁·a₂>a₀·a₃.

В даному випадку: а₀ = 0,005 > 0; а₁·a₂ = 0,51·1 = 0,51; a₀·a₃ = 0,005·600 = 3; 0,51<3. Умова стійкості системи не виконуються, отже за критерієм Гурвіца САК нестійка.

3.4 Побудова амплітудно-фазової частотної характеристики (АФЧХ) та визначення стійкості САК за критерієм Найквіста. Дослідження системи методом D – розбиття

а). Побудуємо амплітудно-частотну характеристику в визначимо стійкість системи по критерію Найквіста:

1) запишемо перехідну характеристику розімкнутої САК

w(s)=.

2) в рівнянні перехідної функції проведемо заміну s→j·ω та проведемо всі можливі перетворення та спрощення, тоді

w(j·ω) =  =

 = = .

Дійсна частина цього виразу

Re(w(j·ω)) =  = Х(ω),

уявна частина – Im(w(j·ω)) =  = У(ω).

3) Побудуємо на комплексній площині (Х0У) криву Найквіста та зробимо висновок про стійкість системи:

У(ω) = 0 → ω = 0 → Х(0) = 0;

У(ω) = 0 → ω = =14 →

Х(14) =  = -6.

По цим точкам побудуємо криву Найквіста (рис. 5).

Критерій Найквіста: Для того щоб замкнута система була стійкою необхідно, щоб годограф розімкненої системи починаючись на дійсній вісі і рухаючись проти годинникової стрілки (при змінній частоті від 0 до ∞) не охоплював точку (-1, j0).

Замкнена САК охоплює точку (-1, j0), що видно на рис. 5. Отже, САК нестійка.

б). Дослідження системи методом D – розбиття

За даними, що були отримані в пункті 3.3 знайдемо критичний коефіцієнт підсилення системи k_кр:

0,51 ≥ k·0,005

k ≤ 102

k = 102 (теоретично розрахований коефіцієнт підсилення).

Використовуючи методику D-розбиття та за допомогою програми MathCad побудуємо межу D-розбиття, обравши за параметр дослідження коефіцієнт підсилення системи.

Характеристичний поліном САК, враховуючи, що параметр, який досліджується, коефіцієнт підсилення:

D(p) = .

Звідси k(p) =  і k(ωj) =

Побудуємо область D-розбиття, знаючи, що Re(k) = , Im(k) = = (див. рис. 6).

На побудованій області D- розбиття можна визначити коефіцієнт підсилення (точка перетину області з дійсною віссю).

Похожие работы

Розрахунок технічних параметрів радіолокаційної станції (РЛС)

Скачать

42182

4

17

... в умовах апріорної невизначеності застосовуються адаптивні системи. Висновок Згідно з технічним завданням на курсову роботу результаті виконання даної курсової роботи були розраховані технічні параметри імпульсної оглядової радіолокаційної станції. А саме було розрахований сигнал, параметри сигналу, параметри антени, реальна розпізнавальна здатність за віддаллю та азимутом, потенційна та ...