Аналіз дискретної САК (ДСАК)

4. Аналіз дискретної САК (ДСАК)

В основі аналізу дискретної САК візьмемо лінійну неперервну САК після корекції з передаточною характеристикою

w(s) = .

4.1 Визначення періоду дискретизації імпульсного елемента

В якості формоутворювача сигналу приймемо екстраполятор нульового порядку.

ω_з = 125с^-1 – максимальна частота в спектрі вхідного сигналу.

За теоремою Котельникова для нормальної роботи системи необхідно, щоб виконувалася умова T_k =  - період дискретизації, відповідно ω_к ≥ 2ω_з – частота дискретизації. Оберемо ω_к ≥ 3·125 = 375 с^-1, тоді T_k ≤ (с).

Виберемо період дискретизації T_k = 0,006с, ω_к = 628 с^-1.

4.2 Визначення передаточної функції розімкнутої та замкнутої ДСАК відносно вхідної дії

w(z) = .

Спочатку розкладемо функцію на простіші дроби:

.

Виконаємо z-перетворення Лапласа отриманої функції:

.

Отже,

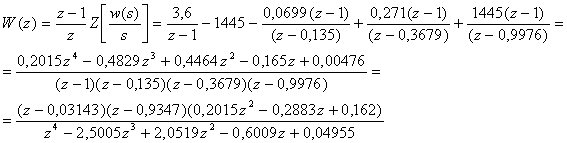
Передатна функція замкненої ДСАК:

.

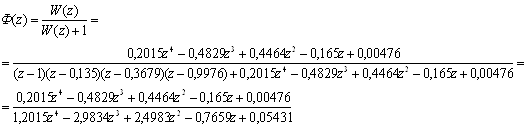4.3 Визначення стійкості отриманої системи по критерію Гурвіца

Знаючи перехідну функцію, знайдемо характеристичне рівняння системи: D(s)=.

Виконаємо білінійне перетворення .

Отримаємо наступне характеристичне рівняння:

На основі отриманих коефіцієнтів характеристичного рівняння побудуємо головний визначник Гурвіца:

D = .

За критерієм Гурвіца для того, щоб система автоматичного керування була стійкою, необхідно та достатньо, щоб при а₀>0 всі визначники Гурвіца були додатними.

а₀=7,5034>0,

Умова стійкості системи виконуються, отже за критерієм Гурвіца САК стійка.

4.4 Побудова логарифмічної псевдочастотної характеристики ДСАК та визначення запасів стійкості

Для побудови логарифмічної псевдочастотної характеристики використаємо передаточну функцію розімкненої системи після корекції та виконання z- перетворення:

Виконаємо 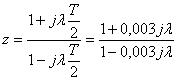, де l - абсолютна псевдочастота, с^-1.

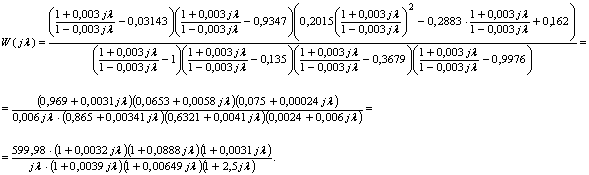
Знайдемо нульову контрольну точку: L₀ = 20lgk = 20lg599,98 = 55,6 дБ.

Визначимо спряжені частоти:

λ₁ =  = 256с^-1, λ₂ =  = 154с^-1,

λ₃ =  = 0,4с^-1, λ₄ =  = 312,5с^-1, λ₅ =  = 11с^-1,

λ₆ =  = 322,6с^-1.

Враховуючи, що до складу системи входить пропорційна, інтегруюча, три аперіодичні ланки першого порядку та три форсуючі ланки отримуємо ЛАХ і ЛФХ для даної САК (рис. 17).

Рис. 17. Логарифмічні частотні характеристики системи.

Знайдемо запаси стійкості системи за ЛАХ та ЛФХ:

· по амплітуді запас стійкості h=µ (DL), тому що ЛФХ не перетинає межу -p.

· по фазі: Δφ = π-Arg(w(j*ω_з)), де ω_з – частота зрізу, коли L(ω_з) = 1, тобто

ω_з = 8. Тоді Δφ = arg(w(j*8) = -38°.

Похожие работы

Розрахунок технічних параметрів радіолокаційної станції (РЛС)

Скачать

42182

4

17

... в умовах апріорної невизначеності застосовуються адаптивні системи. Висновок Згідно з технічним завданням на курсову роботу результаті виконання даної курсової роботи були розраховані технічні параметри імпульсної оглядової радіолокаційної станції. А саме було розрахований сигнал, параметри сигналу, параметри антени, реальна розпізнавальна здатність за віддаллю та азимутом, потенційна та ...