Навигация
Елементи комбінаторики. Початки теорії ймовірностей
ЕЛЕМЕНТИ КОМБІНАТОРИКИ
§ 1. Основні принципи комбінаторики
Досить поширеними є задачі, в яких треба знайти або число можливих розміщень предметів, або число способів, якими можна здійснити деякий вибір, тощо. Такі задачі називають комбінаторними, а галузь математики, яка вивчає теорію скінченних множин, комбінаторикою. Найпростіші задачі комбінаторики вимагають підрахунку числа підмножин заданої множини. Основними принципами (правилами) комбінаторики є принцип суми і принцип добутку.
Принцип суми. Якщо множина A містить п елементів, а множина В - т елементів і А ∩ В = Ø, то множина A U В містить п + т елементів.
Справді, елементи множини А занумеруємо від 1 до п. Серед них немає елементів з множини В, оскільки А ∩ В = 0. Отже, коли ми переходимо до підрахунку елементів, що належать множині В, то починаємо з номера п +1. Далі буде номер п + 2, п + 3 , ..., п + т, оскільки в множині В за умовою т елементів. Цим усі елементи множини A U В буде вичерпано, вони дістануть номери від 1 до п + т.
Правило суми можна сформулювати ще й так: якщо якийсь вибір А можна здійснити п способами, а другий вибір В можна здійснити т способами, то вибір А або В можна здійснити п + т способами.
Принцип суми за індукцією поширюється на к множин.
Принцип добутку. Нехай маємо дві множини:
А={a1, а2, ..., an}, В={b1 b2, ..., bn}.
Тоді множина всіх можливих пар
С={(аi, bi)ا i=1, 2, ..., п; j = 1, 2, ..., m} містить п-т елементів.
Розіб'ємо множину С на множини
С={(а1, b1), (а1, b2), …, (а1, bm) }
С={(а2, b1), (а2, b2), …, (а2, bm) }
…………………………………
С={(аn, b1), (аn, b2), …, (аn, bm) }
Неважко помітити, що множини С1, С2, ..., Сn, попарно не перетинаються і C = Cl UC2 U … UCn. Оскільки кожна з підмножин С1, С2, ..., Сn, містить т елементів, то за принципом суми число елементів в об'єднанні їх дорівнює п • т.
Правило добутку можна сформулювати ще й так: якщо якийсь вибір А можна здійснити п різними способами, а для кожного з цих способів деякий другий вибір В можна здійснити т способами, то вибір А і В у вказаному порядку можна здійснити п • т способами.
Приклад 1. З міста А у місто Б веде 6 шляхів, а з міста Б у місто В 4 шляхи (рис. 298). Скількома шляхами можна проїхати з містам у місто В1 Вибравши один із шести шляхів з міста А у місто Б, далі можемо вибрати шлях від Б до В чотирма способами. Тому на підставі правила добутку дістанемо 6 • 4 = 24.

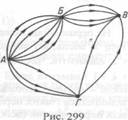
Приклад 2. До міста А, Б і В додамо ще одне місто Г і кілька нових шляхів (рис. 299). Скількома маршрутами тепер можна дістатися з міста А у місто В?
Розглянемо два випадки: шлях проходить через місто Б або через місто Г. Для кожного з цих випадків за правилом добутку неважко під-| рахувати кількість маршрутів (для першого - 24, для другого - 6). За правилом суми маємо остаточно: 24 + 6 = 30. Отже, загальна кількість маршрутів 30.
Приклад 3. У крамниці продають 5 склянок, 3 блюдця і 4 ложки. Скількома способами можна купити два предмети з різними назвами?
Можливими є три випадки: перший - купують склянку з блюдцем, другий - склянку з ложкою, третій - блюдце і ложку. У кожному з цих випадків за правилом добутку неважко підрахувати кількість можливих варіантів: 15, 20 і 12. За правилом суми маємо остаточно: 15 + 20 + 12 = 47.
Сформулюємо тепер принцип (правило) добутку у загальному вигляді.
Нехай треба виконати одну за одною k дій. Якщо першу дію можна виконати n, способами, другу - п2 способами,..., k-ту- пkспособами, то всі k дій разом можуть бути виконані n способами, де п = п2•п2 • ... • пk.
§ 2. Перестановки
Нехай треба підрахувати число способів, за якими можна розмістити в ряд n предметів. Якщо дані предмети розглядати як елементи множини то кожне розміщення є скінченною множиною, елементи якої записано у певному порядку.
Скінченні множини, для яких істотним є порядок елементів, називаються впорядкованими. Вказати порядок розміщення елементів у скінченній множині з п елементів означає поставити у відповідність кожному елементу даної множини певне натуральне число від 1 до п .
Дві впорядковані множини називаються рівними, якщо вони складаються з тих самих елементів і однаково впорядковані. З цього випливає, що множини (а, b, с) і (b, с, а) - це різні впорядковані множини.
Означення. Будь-яка впорядкована множина, що складається з п елементів, називається перестановкою з п елементів.
Перестановки з п елементів складаються з одних і тих самих елементів, а відрізняються одна від одної лише порядком.
Наприклад, з елементів множини А = {1, 2, 3} можна утворити шість перестановок: (1, 2, 3), (1, 3, 2), (2, 1, 3), (2, 3, 1), (3, 1, 2), (3, 2, 1).
Число перестановок у множині з п елементів позначають Рп .
Доведемо, що
Рп=n!, (1)
де п! = 1•2• ... •п .
Для доведення застосуємо метод математичної індукції.
1. Якщо п = 1, маємо Рп =1 = 1!; тобто формула (1) виконується.
2. Припустимо, що для n = 1 рівність Рк = k! виконується (п і k - натуральні числа).
Доведемо, що для п = k +1 виконуватиметься рівність
Рk+1=(к + 1)!
На перше місце можемо поставити будь-який з k + 1 елементів множини. Тоді k місць, які залишилися, можна задавати будь-якою перестановкою з k елементів. Число таких перестановок Рk . Таким чином, перестановку з k + 1 елемента даної множини можна розглядати як пару: на першому місці - елемент множини, на другому - перестановка з k елементів, що залишились (таких перестановок Рk). На підставі принципу добутку число всіх перестановок (всіх таких пар)
Рk+1=(к + 1) Рk , (1)
З формули (2) дістаємо
Рk+1=(к + 1) Рk = Рk • (к + 1) =k! • (k+1)=1•2•…•k• (k+1)=(k+1)!
Приклад 1. Скількома способами можна розмістити в один ряд червону, синю, чорну та зелену фішки?
Р4 = 4! = 1•2•3•4 = 24.
Приклад 2. Скількома способами можна розмістити за столом 10 чоловік?
Р10=10! = 1•2•3•4•5•6•7•8•9•10 = 3628800.
§ 3. Розміщення
Нехай деяка множина складається з п різних елементів.
Означення. Розміщеннями з п елементів по k називаються підмножини, що мають k елементів, вибраних з даних п елементів і розміщених у певному порядку (k<п).
Розміщення можуть відрізнятися одне від одного або самими елементами, або порядком їх розміщення.
Наприклад, нехай маємо три елементи: 1, 2, 3. Тоді розміщення з трьох елементів по два мають вигляд: (1, 2), (1, 3), (2, 1), (3, 1), (2, 3), (З, 2). Розміщення (1, 2) і (2, 1) відрізняються лише порядком. Вони утворюють два різних числа 12 та 21. Розміщення (1, 2) і (1, 3) відрізняються самими елементами. Вони утворюють два різних числа 12 і 13.
Кількість розміщень з даних п елементів по k позначають через Аkn, = k < п.
Доведемо, що
Аkn = n(n-1)(n-2)...(n-(k-1)). (1)
Якщо множина містить п елементів, то при утворенні розміщень по одному елементу таких розміщень буде п (стільки, скільки елементів у множині). Отже, Аkn = п.
Утворимо тепер розміщення з п елементів по два. Для цього візьмемо п розміщень по одному елементу і до кожного розміщення допишемо кожний з решти п -1 елементів даної множини. Таким чином, Аkn = n(n-1).
Застосуємо метод математичної індукції. Припустимо, що для А2n правильною є формула (1). Розміщення з п елементів по k + і можна розглядати як пару: на першому місці будь-яке розміщення з п елементів по k (їх кількість Аkn ), на другому - будь-який елемент з решти п - k елементів. За правилом добутку дістанемо
Аnk +1= Аnk(n-k). (2)
Користуючись формулою (1), маємо
Аnk +1=п(п-1)(п-2)...(п-(k-і))(п-k) = = n(n - 1)(n - 2)...(n- (k -1))(n-(k +1-1)).
Оскільки
![]()
то формулу (1) можна записати ще так:
![]() . (3)
. (3)
Приклад 1. Скількома способами можна вибрати з 10 кандидатів три особи на три різні посади?
Для розв'язування задачі треба знайти число розміщень з 10 елементів по три. Отже, за формулою (1) маємо
A310 =10•9•8 = 720.
Приклад 2. Скільки трицифрових чисел з різними цифрами можна утворити з цифр 0, 1, 2, 3, 4?
Загальна кількість трицифрових чисел з різними цифрами є кількістю
розміщень з 5 елементів по три, тобто А35 = 5 • 4 • 3 = 60. Проте із загальної кількості чисел треба відкинути числа, що починаються з нуля. Таких чисел стільки, скільки можна утворити розміщень з чотирьох цифр по два без нуля, тобто А24 =4•3 = 12. Отже, шукана кількість трицифрових чисел дорівнює 60 - 12 = 48 .
§ 4. Комбінації
Означення. Будь-яка підмножина з k елементів даної множини, яка містіть п елементів, називається комбінацією з п елементів по k.
З одного елемента можна утворити тільки одну комбінацію. З двох елементів а і b можна утворити дві комбінації по одному елементу і тільки одну комбінацію з двох елементів.
З трьох елементів a, b, c можна утворити такі комбінації:
{a}, {b}, {c}, {a,b}, {a,c}, {b,c}, {a,b,c}.
Комбінації з п елементів даної множини по k можна також розглядати як розміщення з п елементів по k, які відрізняються принаймні одним елементом. Виникає запитання, як визначити кількість комбінацій з n елементів по k. Число комбінацій з п по k позначається Сkn . Доведемо, що
![]() . (1)
. (1)
Розглянемо множину, яка складається з п елементів, і комбінації, які складаються з k елементів. Всього комбінацій Сkn. Якщо з кожної такої комбінації утворити всі можливі перестановки (їх буде Рk = k!), то дістанемо всі можливі розміщення з п елементів по к, тобто число Аkn. Отже,
Аkn= Рk •Сkn , (2)
звідки
![]()
Зауважимо, що за означенням покладають 0! = 1. Тому неважко помітити, що С11=1 і Сnn = 1.
Приклад. Збори з 30 осіб вибирають трьох делегатів на конференцію. Скількома способами це можна зробити?
Із множини у 30 осіб треба вибрати підмножину з трьох осіб. Це можна зробити ![]() способами .
способами .
§ 5. Властивості комбінацій
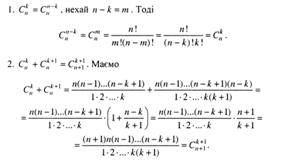
Числа ![]()
![]()
![]()
![]()
![]()
![]() і т.д. зручно записати у вигляді такої трикутної таблиці:
і т.д. зручно записати у вигляді такої трикутної таблиці:
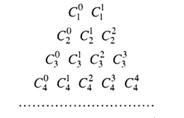
Обчисливши значення кожного символу, дістанемо
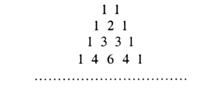
Таку таблицю називають трикутником Паскаля. На «бічних сторонах» цього трикутника стоять одиниці, а "всередині", за властивістю 2, кожне число дорівнює сумі двох чисел, що стоять над ним: 2=1+1; 3=1+2; 4=1+3; 6=3+3 і т.д. Ця властивість дає можливість виписувати послідовно рядки трикутника Паскаля, не обчислюючи перед цим значення символів ![]() .
.
§ 6. Біном Ньютона
З алгебри відомо формули скороченого множення:
(a + b)2 =a2 +2ab + b2,
(а + b)3= а3 + 3a2b + 3ab2 + b2.
Коефіцієнти в правих частинах цих формул збігаються відповідно з другим і третім рядками трикутника Паскаля. Чи буде зберігатись ця закономірність для 4-го, 5-го і т.д. степеня суми?
Щоб відповісти на це запитання, розглянемо вираз (1 + х)п , де п -натуральне число. Запишемо цей вираз як добуток співмножників:
![]()
Розкривши у правій частині дужки, дістанемо многочлен, який можна розмістити за степенями букви х. До цього многочлена ввійдуть усі степені х з показниками від 0 (вільний член) до п. Щоб записати цей многочлен, треба знайти його коефіцієнти. Нехай ціле число k задовольняє нерівності 0 < k < n. З'ясуємо, який коефіцієнт має степінь хк. Цей коефіцієнт дорівнює кількості подібних членів виду хk, які дістанемо, розкривши дужки. Щоб дістати хk, беремо в k дужках другий доданок, а в інших п - k дужках перший доданок, і перемножуємо їх. Такий вибір можна здійснити Сkп способами. Отже, розкривши дужки, матимемо Сkп подібних членів виду хk. Після зведення подібних членів дістанемо відповідний член Сkп xk. Залишається надати k всіх можливих значень k = 0, 1, 2, ..., п, і члени додати. Таким чином, можна записати:
![]()
або, використовуючи символ суми,
![]()
Нарешті, розглянемо вираз (а + b)п . Подамо його у вигляді
![]()
Якщо позначити ![]() = х, то за формулою (2) дістанемо
= х, то за формулою (2) дістанемо
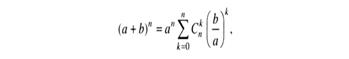
або
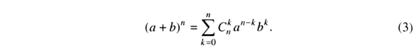
Формула (3) називається формулою бінома Ньютона.
Розгорнутий вигляд формули (3):
![]()
З формули (4) видно, що її коефіцієнти - це рядки трикутника Паскаля.
Поклавши у формулі (4) а = b = 1, дістанемо
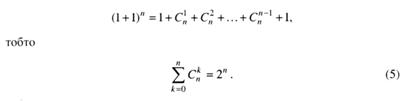
Нехай маємо скінченну множину, яка містить п елементів. Тоді кількість підмножин цієї множини дорівнює 2n. Наприклад, для множини {a,b,c} маємо Ø, {a}, {b}, {c}, {a,b}, {a,c}, {b,c}, {a,b,c}.
ПОЧАТКИ ТЕОРІЇ ЙМОВІРНОСТЕЙ
§ 1. Про предмет теорії ймовірностей
До цього часу розглядалися задачі, в яких результат дії був однозначно визначеним. Проте в житті, у тому числі й в економічній діяльності, виникає потреба розглядати задачі, в яких результат дії не визначається однозначно. Якщо, наприклад, підкинути один раз кубик, не можна передбачити, як саме він упаде. Проте при багаторазовому підкиданні може встановитися певна закономірність. Те саме стосується і процесу обробки якої-небудь деталі. Розміри різних деталей будуть відхилятися від деякої певної величини. Ці відхилення мають випадковий характер, адже розміри щойно виготовленої деталі не дають змоги точно визначити розміри наступної деталі. Проте якщо розглядати партії з великої кількості деталей, то середнє арифметичне розмірів виготовлених деталей у різних партіях є приблизно однаковим.
Подібного роду закономірності і вивчає теорія ймовірностей.
Принципових змін зазнає і сама постановка задачі. Нас вже цікавить не результат конкретного досліду, а те, що саме дістаємо після багаторазового повторення цього досліду.
Теорія ймовірностей вивчає закономірності масових випадкових подій. Вона є основою для вивчення статистичних даних, своєрідним містком між математичним і статистичним аналізами. Нарешті, теорія ймовірностей знаходить широке застосування у задачах економічного характеру. Наведемо приклади.
1. Скільки треба прокласти телефонних ліній до обласного (районного) центру при організації телефонного зв'язку в області (районі)?
Це чисто імовірнісна задача. Адже завчасно не можна передбачити, скільки викликів і в який проміжок часу надійде до центру. Якщо телефонних ліній прокласти замало, то до центру дуже важко буде зателефонувати. Якщо ж їх прокласти забагато, то витрати на організацію телефонного зв'язку будуть надмірними, що є економічно невигідним.
2. Фірма виготовляє телевізори на трьох заводах А, В, С. їй відомо, який процент продукції на кожному заводі становить брак. Фірма хоче визначити ймовірність того, що бракований телевізор виготовлено, скажімо, на заводі Л.
3. Підприємство, яке виробляє продукти споживання, знає, який процент мешканців міста складають жінки і який - мешканці, чий річний заробіток перевищує 6 тис. грн. Підприємство на розвиток своєї ринкової стратегії хоче знати, який процент мешканців міста складають жінки. чий річний заробіток перевищує 6 тис. грн.
§ 2. Основні поняття теорії ймовірностей
Випробуванням (або дослідом) називається експеримент, який можна проводити в однакових умовах будь-яку кількість разів. Результат випробування називається подією або наслідком.
Наприклад, підкидання монети - випробування, поява на ній "герба" -подія. Виготовлення деталей - випробування, поява бракованої деталі -подія.
Події позначають великими буквами латинського алфавіту А, В, С, ....
Означення 1. Випадковою подією називається подія, яка може відбутися або не відбутися під час здійснення певного випробування.
Наприклад, виграш у суперника при грі у шахи, поява бракованого виробу при серійному їх випуску - випадкові події.
Означення 2. Масовими називаються однорідні події, що спостерігаються за певних умов і можуть бути відтворені необмежену кількість разів.
Масовими вважають і ті події, для яких відповідні випробування не можна відтворити, але є можливість спостерігати аналогічні випробування у великій кількості. Наприклад, виклик телефонної станції, прихід суден далекого плавання в порт призначення.
Подія, яка при кожному випробуванні обов'язково відбувається, називається вірогідною. Наприклад, якщо в урні лише білі кулі, то при кожному випробуванні обов'язково вийматиметься тільки біла куля.
Подія, що не може відбутися при жодному випробуванні, називається неможливою. Наприклад, поява чорної кулі, якщо в урні лише білі, є неможливою подією.
Означення 3. Сукупність подій утворює повну групу подій, якщо внаслідок випробування хоч одна з цих подій напевно відбудеться (наприклад, поява 1, 2, 3, 4, 5, 6 очок під час кидання грального кубика).
Якщо повна група складається з двох подій, то такі події називаються протилежними і позначаються А і Ặ.
Означення 4. Події А1 , А2 , ... , Ап називаються попарно несумісними у даному випробуванні, якщо ніякі дві з них не можуть відбутися разом.
Поява 1, 2, 3, 4, 5, 6 очок під час одного кидання грального кубика - приклад множини з шести несумісних подій.
Події А1, А2, ... , Ап можуть бути рівноможливими. Під рівноможливими розуміють такі події, кожна з яких не має ніяких переваг у появі частіше за іншу під час багаторазових випробувань, що проводяться за однакових умов.
Найважливішим поняттям теорії ймовірностей як галузі математики є поняття ймовірності випадкової події.
Ймовірність - числова характеристика появи випадкової події за певної умови, яка може бути відтворена необмежену кількість разів. Розглянемо поняття ймовірності грунтовніше.
§ 3. Класична ймовірність
Нехай маємо 100 деталей, з яких 97 стандартних і 3 браковані. Дослід полягає в тому, що навмання беруть одну деталь. Не можна наперед сказати, якою буде взята деталь - стандартною чи бракованою. Оскільки ми можемо вибирати лише одну яку-небудь деталь, то поява стандартної чи бракованої деталі - випадкові події, які утворюють повну групу з 100 несумісних і рівноможливих подій. З цих 100 випробувань появі стандартної деталі сприяють 97 наслідків, а появі бракованої- 3 наслідки. Нехай А -подія, яка полягає у виборі стандартної деталі, а В - бракованої. Тоді числа 97/100 і 3/100 характеризують можливість здійснення відповідно події А чи В. Ці числа називають ймовірностями подій А і В і позначають
![]()
Означення. Ймовірністю випадкової події називають відношення кількості наслідків випробувань, які сприяють появі цієї події, до загальної кількості всіх рівноможливих несумісних наслідків, які утворюють повну групу подій.
Позначають
![]() (1)
(1)
де п - загальна кількість всіх рівноможливих результатів експерименту;
т - кількість результатів експерименту, сприятливих для події А.
Розглянуте означення ймовірності називають класичним. Із класичного означення ймовірності випливають такі властивості:
1. Ймовірність кожної події А є невід'ємним числом, що не перевищує одиниці. Справді, число т випробувань, сприятливих для події А, справджує нерівності 0 < т < п , звідки ![]() тобто
тобто ![]()
Похожие работы
... нтуватися на використання підручників [53; 54; 5]. У класах фізико-математичного спрямування доцільно орієнтуватись на використання підручників [53; 54; 5; 1]. РОЗДІЛ 2 ОСОБЛИВОСТІ ВИВЧЕННЯ МАТЕМАТИКИ У ПРОФІЛЬНИХ КЛАСАХ В СУЧАСНИХ УМОВАХ 2.1. ОСНОВНІ ПОЛОЖЕННЯ ПРОФІЛЬНОЇ ДИФЕРЕНЦІАЦІЇ НАВЧАННЯ МАТЕМАТИКИ Математика є універсальною мовою, яка широко застосовується в усіх ...
... пошуку адекватного рішення задачі й ін. Особливості технічного мислення показані в роботах С.М.Василевського, П. М. Якобсона, Т. В. Кудрявцева, И. С. Якіманської [5]. Дані, отримані авторами, дозволяють визначити технічне мислення як процес рішення визначеного типу задач, зв'язаного з оперуванням специфічними (технічними) образами в статично-динамічному сполученні. На основі специфіки техні ...
... ситуацію прийняття рішення (аналітичні методи та частково методи математичного програмування); 2) методи, що застосовуються в умовах імовірностної визначеності інформації про ситуацію прийняття рішення (статистичні методи та частково методи математичного програмування); 3) методи, що застосовуються в умовах невизначеності інформації про ситуацію прийняття рішення (теоретико-ігрові методи, які ...
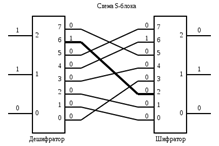
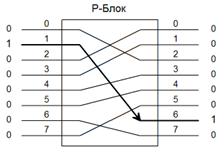
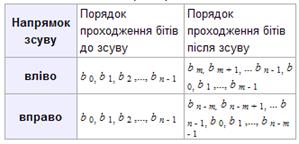
... захисту необхідно виявити можливі погрози безпеці інформації, оцінити їх наслідки, визначити необхідні заходи і засоби захисту і оцінити їх ефективність. [25] 1.3 Криптографічні методи захисту інформації Криптографічний захист інформації — вид захисту інформації, що реалізується за допомогою перетворень інформації з використанням спеціальних даних (ключових даних) з метою приховування (або ...


0 комментариев