Навигация
Принцип оптимальності для задачі оптимального керування з фіксованим часом і вільним правим кінцем
3 Принцип оптимальності для задачі оптимального керування з фіксованим часом і вільним правим кінцем
Розглянемо автономну систему
![]() ,(6)
,(6)
з цільовим функціоналом
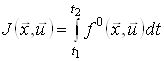 ,(7)
,(7)
у якому початковий і кінцевий моменти часу ![]() і
і ![]() задані, і заданий початковий стан
задані, і заданий початковий стан ![]() .
.
Починаючи з будь-якого моменту часу ![]() , відрізок оптимальної траєкторії
, відрізок оптимальної траєкторії ![]() ,
, ![]() від точки
від точки ![]() до точки
до точки ![]() також є оптимальною траєкторією.
також є оптимальною траєкторією.
Відносно початкового відрізка оптимальної траєкторії до точки ![]() можна стверджувати, що цей відрізок є оптимальною траєкторією, лише у тому випадку, коли точка
можна стверджувати, що цей відрізок є оптимальною траєкторією, лише у тому випадку, коли точка ![]() фіксована (наприклад, у багатоточкових задачах керування), тобто коли за умовами припустима траєкторія обов'язково повинна проходити через точку
фіксована (наприклад, у багатоточкових задачах керування), тобто коли за умовами припустима траєкторія обов'язково повинна проходити через точку ![]() . Якщо ж задана тільки початкова точка
. Якщо ж задана тільки початкова точка ![]() , то відрізок оптимальної траєкторії може і не бути оптимальною траєкторією, тобто може не доставляти оптимальне значення функціоналу (7).
, то відрізок оптимальної траєкторії може і не бути оптимальною траєкторією, тобто може не доставляти оптимальне значення функціоналу (7).
4 Рівняння Беллмана в задачі з фіксованим часом і вільним правим кінцем
Розглянемо систему з законом руху (6) і критерієм оптимальності (2). Початковий стан системи заданий:
![]() ,(8)
,(8)
час руху ![]() відомий, а кінцевий стан
відомий, а кінцевий стан ![]() – невідомий. Побудована таким чином задача – це задача з фіксованим часом і вільним правим кінцем.
– невідомий. Побудована таким чином задача – це задача з фіксованим часом і вільним правим кінцем.
Позначимо через ![]() ,
, ![]() оптимальну траєкторію, яка відповідає оптимальному керуванню
оптимальну траєкторію, яка відповідає оптимальному керуванню ![]() . Зафіксуємо деякий момент часу
. Зафіксуємо деякий момент часу ![]() і відповідну йому точку
і відповідну йому точку ![]() на оптимальній траєкторії. Відповідно до принципу оптимальності, відрізок траєкторії
на оптимальній траєкторії. Відповідно до принципу оптимальності, відрізок траєкторії ![]() від точки
від точки ![]() до точки
до точки ![]() є оптимальною траєкторією і надає найменшого значення функціоналу
є оптимальною траєкторією і надає найменшого значення функціоналу
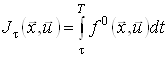
серед всіх припустимих процесів ![]() на відрізку часу
на відрізку часу ![]() з початковим станом
з початковим станом ![]() , тобто
, тобто
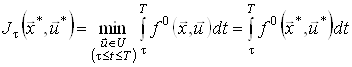 .
.
Припустимо, що для будь-якої точки ![]() фазового простору
фазового простору ![]() і будь-якого моменту часу
і будь-якого моменту часу ![]() існує оптимальна траєкторія з початковою умовою
існує оптимальна траєкторія з початковою умовою ![]() , яка надає найменшого значення функціоналу
, яка надає найменшого значення функціоналу ![]() . Позначимо це мінімальне значення через
. Позначимо це мінімальне значення через
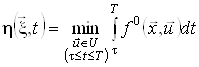 .
.
Функція ![]() , що задана у всіх точках
, що задана у всіх точках ![]() , простору
, простору ![]() ,
, ![]() , називається функцією Беллмана.
, називається функцією Беллмана.
Припустимо, що ![]() ,
, ![]() , – оптимальний процес і оптимальна траєкторія
, – оптимальний процес і оптимальна траєкторія ![]() задовольняє початковій умові
задовольняє початковій умові ![]() . Тоді
. Тоді
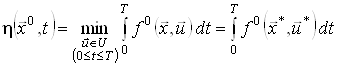
визначає цільовий функціонал (2) початкової задачі.
Розглянемо приріст ![]() і відповідний йому момент часу
і відповідний йому момент часу ![]() . Очевидно, що останнє співвідношення можна переписати так:
. Очевидно, що останнє співвідношення можна переписати так:
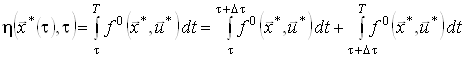 .(9)
.(9)
Відповідно до принципу оптимальності, відрізок оптимальної траєкторії від точки ![]() до точки
до точки ![]() також є оптимальною траєкторією, тобто
також є оптимальною траєкторією, тобто
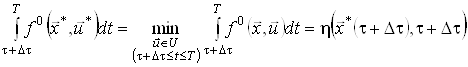 ,
,
тому співвідношення (9) можна переписати у вигляді
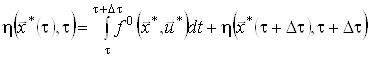 .(10)
.(10)
Очевидно, що другий доданок в (10) залежить від стану системи ![]() (оскільки оптимальне значення функціонала
(оскільки оптимальне значення функціонала ![]() залежить від початкового стану системи
залежить від початкового стану системи ![]() і для кожного початкового стану
і для кожного початкового стану ![]() оптимальне значення функціонала
оптимальне значення функціонала ![]() різне). У цей стан
різне). У цей стан ![]() , у свою чергу, система попадає під дією керування
, у свою чергу, система попадає під дією керування ![]() , яке діє на інтервалі часу
, яке діє на інтервалі часу ![]() . Отже, значення
. Отже, значення ![]() залежатиме від вибору керування на відрізку
залежатиме від вибору керування на відрізку ![]() .
.
Дійсно, розглянемо різні припустимі керування ![]() на відрізку
на відрізку ![]() . Їм відповідатиме набір траєкторій
. Їм відповідатиме набір траєкторій ![]() , що виходять із точки
, що виходять із точки ![]() , яка лежить на оптимальній траєкторії
, яка лежить на оптимальній траєкторії ![]() . На кожній траєкторії із цього набору фазова точка в момент часу
. На кожній траєкторії із цього набору фазова точка в момент часу ![]() попаде в деякий стан
попаде в деякий стан ![]() .
.
Виберемо керування ![]() на відрізку
на відрізку ![]() так, щоб траєкторія
так, щоб траєкторія ![]() на цьому відрізку була оптимальною. Це оптимальне керування в загальному випадку різне для кожної траєкторії пучка. Очевидно, що вибираючи одне – оптимальне – серед всіх можливих керувань
на цьому відрізку була оптимальною. Це оптимальне керування в загальному випадку різне для кожної траєкторії пучка. Очевидно, що вибираючи одне – оптимальне – серед всіх можливих керувань ![]() ,
, ![]() для кожної із траєкторій
для кожної із траєкторій ![]() , ми фіксуємо подальший стан кожної із них і при цьому одержуємо мінімальне значення функціонала
, ми фіксуємо подальший стан кожної із них і при цьому одержуємо мінімальне значення функціонала
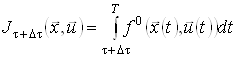 ,
,
яке дорівнює
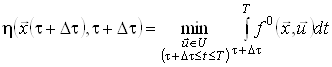 .
.
Очевидно, що це значення залежить від стану ![]() . А оскільки, як було встановлено раніше, стан
. А оскільки, як було встановлено раніше, стан ![]() залежав від вибору керування
залежав від вибору керування ![]() на відрізку
на відрізку ![]() , то й значення
, то й значення ![]() також залежатиме від того, яким було обрано керування
також залежатиме від того, яким було обрано керування ![]() ,
, ![]() .
.
Розглянемо значення функціонала ![]() на траєкторіях з набору, побудованого вище при
на траєкторіях з набору, побудованого вище при ![]() . Оскільки відрізок кожної траєкторії
. Оскільки відрізок кожної траєкторії ![]() від точки
від точки ![]() до точки
до точки ![]() є оптимальним відповідно до принципу максимуму, то значення функціонала дорівнює
є оптимальним відповідно до принципу максимуму, то значення функціонала дорівнює
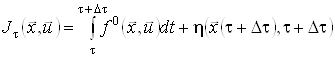 .(11)
.(11)
Ясно, що останнє співвідношення різне для кожної з траєкторій ![]() і відповідного цій траєкторії керування
і відповідного цій траєкторії керування ![]() на відрізку
на відрізку ![]() . Виберемо серед всіх значень
. Виберемо серед всіх значень ![]() мінімальне. Оскільки обидва доданки в (11) залежать тільки від вибору керування
мінімальне. Оскільки обидва доданки в (11) залежать тільки від вибору керування ![]() на інтервалі
на інтервалі ![]() , то і мінімальне значення (11) залежатиме тільки від вибору керування на цьому інтервалі, тобто
, то і мінімальне значення (11) залежатиме тільки від вибору керування на цьому інтервалі, тобто
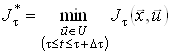 .
.
Побудований набір траєкторій є підмножиною більш широкої множини всіх припустимих функцій, на яких шукається найменше значення функціонала ![]() . Тому в загальному випадку має місце нерівність
. Тому в загальному випадку має місце нерівність
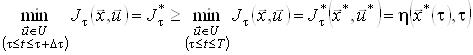 .(12)
.(12)
Але оскільки оптимальна траєкторія ![]() належить до побудованого набору траєкторій, то в співвідношенні (12) насправді має місце рівність, тобто
належить до побудованого набору траєкторій, то в співвідношенні (12) насправді має місце рівність, тобто
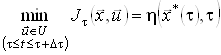 .
.
Звідси з урахуванням (11) одержимо
 , (13)
, (13)
тобто оптимізація процесу проводиться тільки для ![]() , тому що для
, тому що для ![]() траєкторія вже оптимальна.
траєкторія вже оптимальна.
Розглянемо поведінку останнього співвідношення при ![]() , тобто коли інтервал
, тобто коли інтервал ![]() , на якому шукається оптимальне керування, звужується до точки. Відповідно до закону руху
, на якому шукається оптимальне керування, звужується до точки. Відповідно до закону руху
![]() .
.
Вважатимемо, що функція Беллмана ![]() неперервно диференційована по всіх своїх аргументах. Тоді
неперервно диференційована по всіх своїх аргументах. Тоді
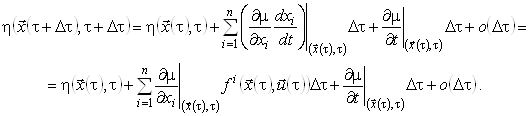 (14)
(14)
Позначатимемо далі
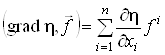 .
.
Співвідношення (14) з урахуванням цього позначення набуде вигляду
![]() .
.
Використовуючи останнє співвідношення, рівність (13) можна подати у вигляді
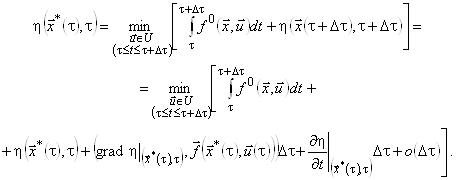 (15)
(15)
Оскільки функції ![]() і
і 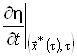 у правій частині (15) не залежать від
у правій частині (15) не залежать від ![]() , їх можна винести за знак мінімуму. Після скорочень одержимо
, їх можна винести за знак мінімуму. Після скорочень одержимо
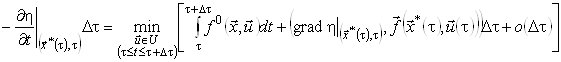 .
.
Припустимо, що функція ![]() є неперервною на відрізку
є неперервною на відрізку ![]() . Розділивши останнє співвідношення на
. Розділивши останнє співвідношення на ![]() , при
, при ![]() одержимо
одержимо
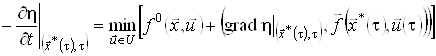 .(16)
.(16)
Останнє співвідношення називається рівнянням Беллмана. Воно є аналогом рекурентних рівнянь Беллмана дискретної задачі оптимального керування для випадку неперервної системи.
Замінивши ![]() на
на ![]() , де
, де ![]() – оптимальна траєкторія, одержимо з (16)
– оптимальна траєкторія, одержимо з (16)
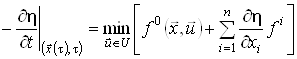 .(17)
.(17)
До рівняння Беллмана додаються крайові умови, що випливають безпосередньо з визначення функції Беллмана:
![]() .(18)
.(18)
Рівняння Беллмана – це диференціальне рівняння в частинних похідних відносно функції ![]() . Але це рівняння не є лінійним через наявність у (17) операції мінімізації. Фактично це означає підстановку в рівняння такого
. Але це рівняння не є лінійним через наявність у (17) операції мінімізації. Фактично це означає підстановку в рівняння такого ![]() , на якому досягається мінімум і яке змінюється в залежності від значень
, на якому досягається мінімум і яке змінюється в залежності від значень ![]() і
і ![]() .
.
Похожие работы
... у формулу (2.11) і визначити наступний стан системи . Для зміненого стану знайти оптимальне управління , підставити у формулу (2.11) і так далі. Для і-гo стану , знайти і і т.д. [1]. 3. Оптимальний розподіл інвестицій, як задача динамічного програмування Інвестор виділяє кошти в розмірі умовних одиниць, котрі повинні бути розподілені між -підприємствами. Кожне і-те підприємство при і ...
... стратегія володіє тим властивістю, що стосовно будь-якого первісного стану після деякого етапу рішення сукупність наступних рішень повинна становити оптимальну стратегію. Цей принцип оптимальності лежить в основі всієї концепції динамічного програмування. Саме завдяки йому вдається при наступних переходах випробовувати не всі можливі варіанти, а лише оптимальні виходи. Рекурентні співвідношення ...
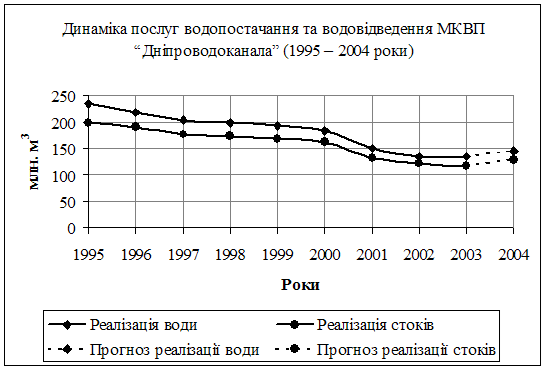
... "Баланс" за 2007 – 2008 роки (додаток В); - форма № 2 "Звіт про фінансові результати" за 2007 – 2008 роки (додаток Г). 3 Підвищення ефективності виробництва МКВП "Дніпроводоканал" на підставі методів Економіко-математичного моделювання У грудні 2008 року Дніпропетровський міськвиконком та комунальне Підприємство "Дніпроводоканал", яке знаходиться у власності м. Дніпропетровська ...
... ічно зростають показники ефективноств їх діяльності. Науково-дослідні інститути закордоном працюють над новими моделями, які раніше чи пізніше пристосуються до практики управління. Щоб якимось чином впорядкувати та зробити більш наочним питання про сфери застосування тих чи інших моделей і методів наведемо таблицю (див. табл.7).Таблиця 7: Сфери застосування моделей і методів обгруниування управлі ...



0 комментариев