Навигация
Рівняння Беллмана в задачі з фіксованими кінцями та вільним часом
13680
знаков
0
таблиц
1
изображение
5 Рівняння Беллмана в задачі з фіксованими кінцями та вільним часом
Додамо до задачі (2), (6), (9) умову закріплення правого кінця траєкторії 
, де 
– задано, а 
– невідомо. У цьому випадку функція Беллмана залежатиме тільки від поточного стану системи. Дійсно, згідно з визначенням функції Беллмана
.
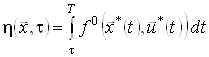Якщо підінтегральна функція не залежить від 
, то значення інтеграла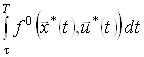 
при фіксованих 
і 
залежить тільки від довжини інтервалу інтегрування 
, який можна визначити з автономної системи (6), якщо відомі точки 
і 
фазової траєкторії. Тому різниця – це функція від аргументів і , а 
не залежить явно від . У цьому випадку 
і рівняння Беллмана для задачі із закріпленими кінцями набуває вигляду
.
6 Рівняння Беллмана в задачі швидкодії
Розглянемо задачу оптимальної швидкодії з фіксованими кінцями і вільним часом, закон руху якої має вигляд (6) і задані початковий стан 
та кінцевий стан 
. Час невідомий і його потрібно знайти з умови мінімізації цільового функціонала
.
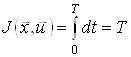У задачі з фіксованими кінцями і вільним часом функція Беллмана залежить тільки від поточного стану системи і не залежить від моменту, починаючи з якого розглядається її еволюція (доведення аналогічно п. 5), тобто 
.
Вважатимемо, що функція 
неперервна на будь-якому відрізку 
і для будь-якої точки фазового простору 
і будь-якого моменту часу 
існує оптимальна траєкторія, а функція неперервно диференційована за своїми аргументами. Тоді необхідна умова оптимальності у вигляді рівняння Беллмана (17), (18) для даної задачі матиме вигляд:
,
або
за заданих крайових умов 
.
Очевидно, що якщо процес 
– оптимальний, то, будучи підставленим у рівняння Беллмана, він дасть тотожність
.
Зауваження. Оскільки функція Беллмана 
дорівнює мінімальному значенню цільового функціонала, що характеризує перехід системи в кінцевий стан зі стану 
, то в задачі оптимальної швидкодії ця функція показує оптимальний час переходу зі стану у фіксований стан 
.
Похожие работы
... у формулу (2.11) і визначити наступний стан системи . Для зміненого стану знайти оптимальне управління , підставити у формулу (2.11) і так далі. Для і-гo стану , знайти і і т.д. [1]. 3. Оптимальний розподіл інвестицій, як задача динамічного програмування Інвестор виділяє кошти в розмірі умовних одиниць, котрі повинні бути розподілені між -підприємствами. Кожне і-те підприємство при і ...
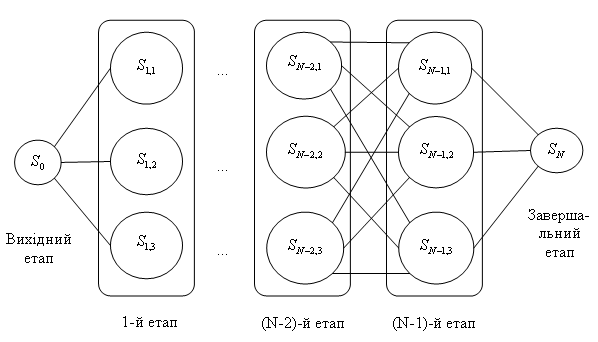
... стратегія володіє тим властивістю, що стосовно будь-якого первісного стану після деякого етапу рішення сукупність наступних рішень повинна становити оптимальну стратегію. Цей принцип оптимальності лежить в основі всієї концепції динамічного програмування. Саме завдяки йому вдається при наступних переходах випробовувати не всі можливі варіанти, а лише оптимальні виходи. Рекурентні співвідношення ...
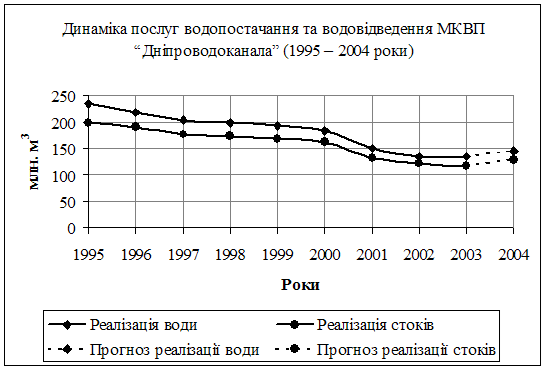
... "Баланс" за 2007 – 2008 роки (додаток В); - форма № 2 "Звіт про фінансові результати" за 2007 – 2008 роки (додаток Г). 3 Підвищення ефективності виробництва МКВП "Дніпроводоканал" на підставі методів Економіко-математичного моделювання У грудні 2008 року Дніпропетровський міськвиконком та комунальне Підприємство "Дніпроводоканал", яке знаходиться у власності м. Дніпропетровська ...
... ічно зростають показники ефективноств їх діяльності. Науково-дослідні інститути закордоном працюють над новими моделями, які раніше чи пізніше пристосуються до практики управління. Щоб якимось чином впорядкувати та зробити більш наочним питання про сфери застосування тих чи інших моделей і методів наведемо таблицю (див. табл.7).Таблиця 7: Сфери застосування моделей і методів обгруниування управлі ...
0 комментариев