Навигация
Вычислить параметры зависимости a и b методом наименьших квадратов
2.1. Вычислить параметры зависимости a и b методом наименьших квадратов.
2.2. Оценить соответствие построенной зависимости статистическим данным.
| Вариант 7 | x | 109 | 107 | 108 | 111 | 106 | 105 | 104 |
| y | 234 | 235 | 236 | 237 | 238 | 239 | 240 |
Выполнение задания
Для выполнения заданий используем пакет электронных таблиц Excel.
2.1 Блок исходных данных формируется в первых двух столбцах (A3:B9).
2.2 Вводится гипотеза, что между фактором Х и показателем Y существует линейная стохастическая зависимость ![]() = a · X +b
= a · X +b
Оценки параметров a и b парной регрессии вычисляются по формулам
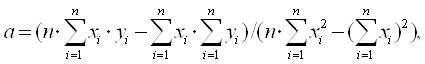
![]()
За блоком исходных данных находится блок промежуточных расчетов.
Для нахождения произведения ![]() в ячейку C3 вводится формула =A3·B3. Далее копируем полученную формулу в другие ячейки столбца C. Значения
в ячейку C3 вводится формула =A3·B3. Далее копируем полученную формулу в другие ячейки столбца C. Значения ![]() вычисляем в столбце D.
вычисляем в столбце D.
Для определения сумм столбцов используем кнопку автосуммирования на панели инструментов ∑. После установления курсора на ячейку A10 нажимаем ∑ на панели инструментов, выделяем диапазон ячеек А3:А9, нажимаем Enter. Введенная формула копируется в необходимые ячейки 10-ой строки. Средние значения X, Y вычисляются в ячейках D11, D12 с использованием встроенной статистической функции СРЗНАЧ ():
=СРЗНАЧ(A3:A9) и =СРЗНАЧ(B3:B9).
В ячейки В12, В13 вводятся формулы для определения оценок параметров соответственно a и b.
=(B11*C10-B10*A10)/(B11*D10-A10^2) – для параметра а;
=D12-B12*D11 – для параметра b.
а=-0,602, b=301,55,
уравнение регрессии:
Y=-0,602×Х + 301,55
2.3. Для вычисления расчетных значений ![]() (і=
(і=![]() ) в ячейку E3 вводим формулу
) в ячейку E3 вводим формулу ![]() с абсолютными ссылками координат-параметров a и относительной ссылкой координаты
с абсолютными ссылками координат-параметров a и относительной ссылкой координаты ![]() . Полученную формулу в ячейке E3 копируем в блок E4:E9 В ячейке E10 будет находиться сумма блока E3:E9. Поскольку математическое ожидание отклонения фактических данных от расчетных равняется нулю, то при правильном выполнении расчетов значения ячеек B10 и E10 будут совпадать.
. Полученную формулу в ячейке E3 копируем в блок E4:E9 В ячейке E10 будет находиться сумма блока E3:E9. Поскольку математическое ожидание отклонения фактических данных от расчетных равняется нулю, то при правильном выполнении расчетов значения ячеек B10 и E10 будут совпадать.
Для определения адекватности принятой эконометрической модели экспериментальным данным воспользуемся F-критерием Фишера. Расчетное значение критерия Фишера определяется по формуле:
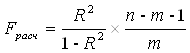
Значение ![]() вычисляем соответственно в блоках F3:F9, G3:G9, H3:H9, а их суммы в блоке F10:H10.
вычисляем соответственно в блоках F3:F9, G3:G9, H3:H9, а их суммы в блоке F10:H10.
Значения коэффициента детерминации 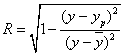 вычисляется в ячейке F11 с использованием встроенной математической функции КОРЕНЬ.
вычисляется в ячейке F11 с использованием встроенной математической функции КОРЕНЬ.
Для оценки коэффициента корреляции
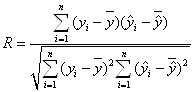
в ячейку I3 вводим формулу для вычисления значения ![]() и копируется в блок I4:I9. Сумма блока I3:I9 вычисляется в ячейке I10.
и копируется в блок I4:I9. Сумма блока I3:I9 вычисляется в ячейке I10.
Значения коэффициента корреляции вычисляется в ячейке F13.
Kkor=-0,672194
Расчетное значение критерия Фишера: Fроз= 4,121495
Табличное значение F-критерия для вероятностей P=0,95 и числа степеней свободы
K1 = m = 1,
K2 = n – m – 1 = n – 2 = 7 – 2 = 5 равняется: F(0.95;1;5)= 5,99
Поскольку ![]() , то с надежностью P=0,95 эконометрическую модель можно считать неадекватной экспериментальным данным. Об этом также говорит невысокое значение коэффициента корреляции Kkor=-0,672194
, то с надежностью P=0,95 эконометрическую модель можно считать неадекватной экспериментальным данным. Об этом также говорит невысокое значение коэффициента корреляции Kkor=-0,672194
Таблица с расчетными данными:
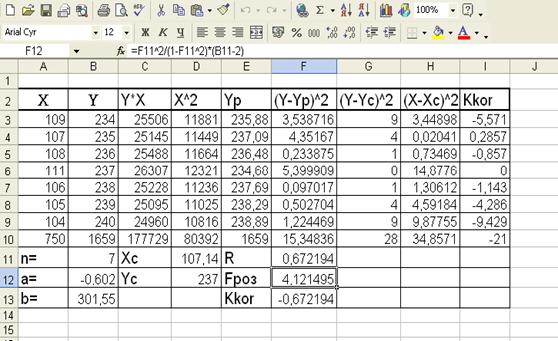
Задача 3
Предприятие имеет 7 филиалов по реализации продукции. Руководству предприятия необходимо, исходя из статистических данных об их деятельность оценить силу зависимости товарооборота (Y) от факторов: объема торговой площади (S), интенсивности потока покупателей (N) и стоимости основных фондов (F). С помощью линейной регрессионной модели вида
![]() ,
,
установить связь между товарооборотом и двумя наиболее существенными факторами.
3.1. Вычислить коэффициенты корреляции между результативным признаком Y и факторами: S, N и F.
3.2. Определить два фактора, которые наиболее влияют на товарооборот Y.
3.3. Вычислить параметры регрессионной модели а , b , с методом наименьших квадратов.
3.4. Оценить соответствие построенной зависимости статистическим данным.
| Вариант 7 | S, кв.м. | 15 | 23 | 18 | 18 | 19 | 17 | 23 |
| N, чел. | 567 | 568 | 569 | 345 | 234 | 453 | 345 | |
| F,тис.грн. | 10 | 7 | 11 | 28 | 15 | 10 | 57 | |
| Y,млн.грн | 0,25 | 0,24 | 0,23 | 0,28 | 0,23 | 0,27 | 0,27 |
Выполнение задания
Похожие работы
... частности, разрабатываются способы уменьшения дисперсии используемых случайных величин, в результате чего уменьшается ошибка, допускаемая при замене искомого математического ожидания а его оценкой а*. §2. Оценка погрешности метода Монте-Карло. Пусть для получения оценки a* математического ожидания а случайной величины Х было произведено n независимых испытаний (разыграно n возможных значений Х) ...
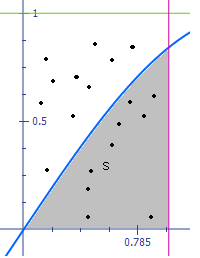
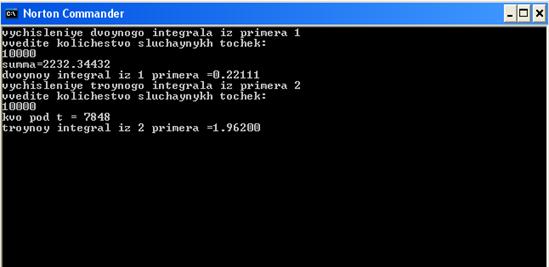
... прийнятної точності необхідна велика кількість статистичних випробувань. Теорія методу Монте-Карло вивчає способи вибору випадкових величин для вирішення різних завдань, а також способи зменшення дисперсії випадкових величин. 3. Програма обчислення кратного інтеграла методом Монте-Карло Обчислити певний інтеграл . за методом “Монте-Карло” по формулі , де n – число випробувань ;g(x) – щі ...
... Впрочем, для наиболее распространённых псевдослучайных чисел период столь велик, что превосходит любые практические потребности. Подавляющее большинство расчётов по методу Монте-Карло осуществляется с использованием псевдослучайных чисел. Значения любой случайной величины можно получить путём преобразования значений одной какой-либо случайной величины. Обычно роль такой случайной величины играет ...
етка – одно из простейших средств получения случайных чисел с хорошим равномерным распределением, на использовании которых основан этот метод. Метод Монте – Карло это статистический метод. Его используют при вычислении сложных интегралов, решении систем алгебраических уравнений высокого порядка, моделировании поведения элементарных частиц, в теориях передачи информации, при исследовании сложных ...

0 комментариев