Навигация
Исходные данные факторов размещаем в блоке B2:D18, а показатели в столбце E2:E8
12333
знака
4
таблицы
20
изображений
3.1. Исходные данные факторов размещаем в блоке B2:D18, а показатели в столбце E2:E8.
3.2. В блоке A13:C14 используя встроенную функции Excel =КОРРЕЛ() находим коэффициенты корреляции между показателем Y и факторами Х1, Х2, Х3
| Корф. кор.-ции | ||
| Y - X1 | Y - X2 | Y - X3 |
| 0,208604 | -0,60362 | -0,04747 |
3.3. Как видно из корреляционной матрицы для регрессионной модели можно выбрать две переменные – Х1 и Х2, так как для них значения коэффициента корреляции с показателем близки к 1 и равны 0,208604и -0,60362 соответственно.
3.4. Допустим, что между показателем Y и факторами Х1, Х2 существует линейная зависимость 
. Найдем оценки параметров, используя метод наименьших квадратов (в матричных операциях). Запишем систему нормальных уравнений в матричной форме
, где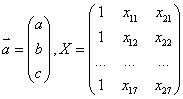 
Если помножить матричное уравнение слева на матрицу 
, то для оценки параметров вектора 
получим формулу
.
Нахождение оценок параметров регрессии:
1. Находим транспонированную матрицу 
в блоке E13:K15 по отношению к матрице 
в блоке A2:C8, используя в категории "Ссылки и массивы" встроенную функцию ТРАНСП(A2:C8).
2. Находим произведение матриц 
в блоке A18:C20, используя встроенную математическую функцию МУМНОЖ(блок данных первой матрицы A18:C20; блок данных второй матрицы A2:C8).
3. Обратную матрицу 
находим в блоке D18:F20, используя встроенную математическую функцию =МОБР(A18:C20).
4. Произведение матриц 
находим в блоке H18:H20, встроенную математическую функцию =МУМНОЖ(E13:K15;E2:E8).
5. Оценки вектора находим в блоке J39:J41, встроенную математическую функцию =МУМНОЖ(D18:F20;H18:H20).
| [XT][X]-1[XT]Y |
| 0,32512 |
| 0,00040 |
| -0,00005 |
a= 0,00040, b= -0,00005, c= 0,32512.
Уравнение регрессии:
Y=0,00040X1 + -0,00005X2 + 0,32512
3.5. Проверим адекватность принятой модели экспериментальным данным с помощью критерия Фишера. Расчетные значения Yрасч считаем в столбце F по формуле Yрасч=0,00040Х1+-0,00005Х2+0,32512..
Рассчитываем F-статистику Фишера с m и (n- m- 1) степенями свободы:
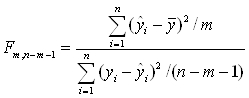
где m — количество факторов, которые вошли в модель; m=2
n – общее количество наблюдений; n=7
В ячейках F2:F10 находятся расчетные значения показателя, а в ячейках G2:G10 квадраты их отклонений от экспериментальных значений.
В ячейках H2:H10 квадраты отклонений от среднего значения.
Расчетное значение Fрасч= 1,19895497
По F- таблице Фишера находим критическое значение Fкр с m и (n-m-1) степенями свободы: Fкрит(0,95;2;4)= 6,94
Расчетное значение критерия 1,19895497 меньше критического, значит с надежностью 
можно считать, что принятая математическая модель неадекватна по экспериментальным данным.
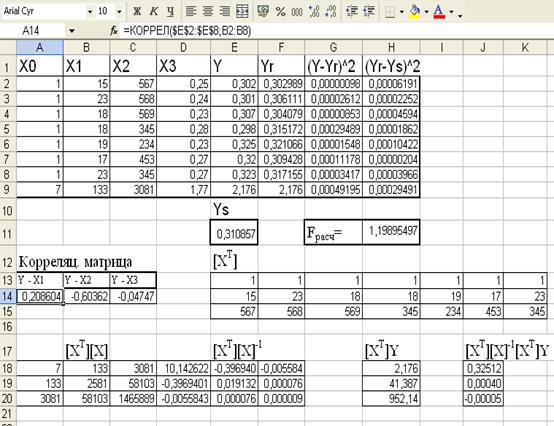
Таблица с расчетными данными:
Похожие работы
... частности, разрабатываются способы уменьшения дисперсии используемых случайных величин, в результате чего уменьшается ошибка, допускаемая при замене искомого математического ожидания а его оценкой а*. §2. Оценка погрешности метода Монте-Карло. Пусть для получения оценки a* математического ожидания а случайной величины Х было произведено n независимых испытаний (разыграно n возможных значений Х) ...
... прийнятної точності необхідна велика кількість статистичних випробувань. Теорія методу Монте-Карло вивчає способи вибору випадкових величин для вирішення різних завдань, а також способи зменшення дисперсії випадкових величин. 3. Програма обчислення кратного інтеграла методом Монте-Карло Обчислити певний інтеграл . за методом “Монте-Карло” по формулі , де n – число випробувань ;g(x) – щі ...
... Впрочем, для наиболее распространённых псевдослучайных чисел период столь велик, что превосходит любые практические потребности. Подавляющее большинство расчётов по методу Монте-Карло осуществляется с использованием псевдослучайных чисел. Значения любой случайной величины можно получить путём преобразования значений одной какой-либо случайной величины. Обычно роль такой случайной величины играет ...
етка – одно из простейших средств получения случайных чисел с хорошим равномерным распределением, на использовании которых основан этот метод. Метод Монте – Карло это статистический метод. Его используют при вычислении сложных интегралов, решении систем алгебраических уравнений высокого порядка, моделировании поведения элементарных частиц, в теориях передачи информации, при исследовании сложных ...
0 комментариев