Сокращение мономиальных систем

1.2 Сокращение мономиальных систем

Пусть : – полиномиальная система, где каждый  – моном, такой, что , где  – неотрицательное целое число. То есть,  может быть описано матрицей . В первую очередь связывается  с Булевой мономиальной системой  и линейной системой  над кольцами . В работе «Булевы мономиальные системы»  называется системой конечных элементов если все конечные циклы  заключаются в фиксированном элементе. Покажем что  – конечный элемент системы тогда, и только тогда, когда  и  – системы конечных элементов.

Определение 1.2.1.

Для , мы определим базис , обозначенный supp(u), равный , где

  

Мономиальная система  порождает Булеву мономиальную систему  на  с параметрами , где  и v=supp(u).

Лемма 1.2.1.

- коммутативная диаграмма.

Доказательство.

Это прямо доказывается тем что supp(f(u))=f(supp(u)).



Так как  на множестве всех  таких, что supp(u)=u, появляется следующие прямые следствия.

Следствие 1.2.1.

Фазовое пространство  – подграф фазового пространства .

Следствие 1.2.2.

Предположим что  – система конечных элементов. Если  – цикл в фазовом пространстве , тогда  для всех .

Пример 1.2.1.

Пусть .

- состоит из всех возможных наборов длины 3 из трёх элементов: 0, 1, 2.

Это наборы:

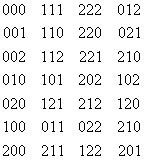
Используя функцию , определим переходы в фазовом пространстве .

000 - ,

001 - ,

002 - ,

010 - ,

020 - ,

100 - ,

200 - ,

111 - ,

110 - ,

112 - ,

101 - ,

121 - ,

011 - ,

211 - ,

222 - ,

220 - ,

221 – ,

202 - ,

212 - ,

022 - ,

122 - ,

012 - ,

021 - ,

210 - ,

102 - ,

120 - ,

210 - ,

201 - ,

Так как , то . Используя эту функцию, определим переходы в фазовом пространстве .

000 - ,

001 - ,

010 - ,

100 - ,

101 - ,

011 - ,

110 - ,

111 - .

На рисунке 1.2.1 и 1.2.2 изображены фазовое пространство системы  и ее «Булеанизяция» , соответственно.

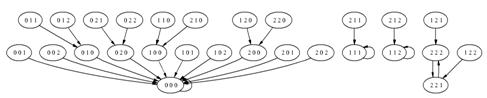
Рис. 1.2.1. Фазовое пространство .

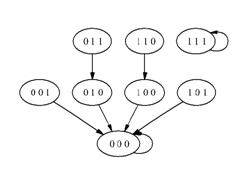
Рис. 1.2.2. Фазовое пространство .

Затем связывается  с  - размерной линейной системой над конечным кольцом. Заметим сначала что  – изоморфный, как Абелева группа, для  через изоморфизм , появляется возможность генератора для циклической группы . В первую очередь обратим внимание, что множество векторов  со всеми ненулевыми вхождениями – постоянны для .

Пусть  – генератор для циклической группы ,и пусть .

Тогда .

Определение 1.2.2.

Обозначим  для .

Видно что  – линейное преобразование - элемента. Но можно рассматривать его, как линейное преобразование для  - элемента, рассматривая  как конечное кольцо, которое обозначим – . То есть, имеется линейное преобразование .

Это доказывает следующую лемму.

Лемма 1.2.2.

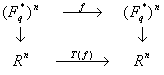 - коммутативная диаграмма.

Обратим внимание, что вертикальные стрелки – изоморфизмы. Это значит, что они сохраняют фазовое пространство структуры, включая длину конечных циклов. В частности, имеется следующее следствие.

Следствие 1.2.3.

Фазовое пространство  изоморфно к подграфу фазового пространства , состоя из всех наборов с базисным вектором .

Пример 1.2.2.

Для мономиальной системы  в примере 1.2.1,  определим , где

.

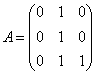Рассчитаем переходы в фазовом пространстве .

000 - ,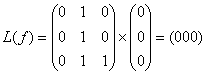

001 - ,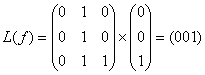

010 - ,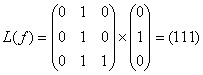

011 - ,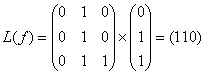

100 - ,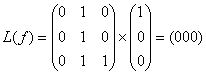

101 - ,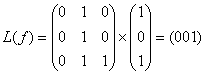

110 - ,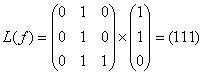

111 - .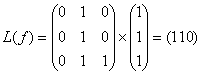

Фазовое пространство  изображено на рисунке 1.2.3.

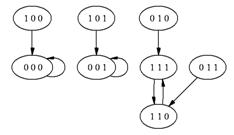
Рис. 1.2.3. Фазовое пространство .

Теорема 1.2.1.

Пусть  – мономиальная динамическая система. Тогда  – система конечных элементов тогда, и только тогда, когда и  – системы конечных элементов.

Доказательство.

Из следствий 1.2.1 и 1.2.3, если  – система конечных элементов, то  и  тоже системы конечных элементов. Для доказательства от противного, предположим что  и  – системы конечных элементов, а  – нет. Для каждого конечного цикла , любой из двух связанных наборов имеет все координаты ненулевые, или все наборы имеют минимум одну нулевую координату. В первом случае из этого следует, что  имеет конечный цикл, той же длины. Следовательно, если  имеет конечный цикл длины большей чем , тогда включаются только наборы имеющие минимум одну нулевую координату.

Пусть  – наборы в конечном цикле. Так как этот конечный цикл должен отображать конечный элемент для  из этого следует, что  имеет тот же самый базисный вектор, то есть, тот же самый образец нулевых вхождений, и отличается только в ненулевых координатах. Кроме того, мономы в ненулевых координатах не включают никакие переменные, соответствующие нулевым координатам. Таким образом, если построить новый набор , заменяя каждый  в , на ,  – будет частью конечного цикла длины, по крайней мере , что является противоречием. Это доказывает теорему.