Навигация
Середні величини та показники варіації
69379
знаков
1
таблица
4
изображения
2. Середні величини та показники варіації
При вивчені масових явищ одна з основних задач статистики є вивчення окремих властивостей кожної сукупності явища. Для того щоб виявити характерні особливості сукупності, використовують середні величини. Середня величина характеризує всю вагу одиниць сукупності.
В статистиці використовують декілька видів середніх величин. Основними серед них є: середня арифметична, середня гармонічна, середня квадратична і середня геометрична
Середня арифметична – основний вид середніх величин. Буває проста і зважена. Проста – це сума індивідуальних значень варіруємої ознак, що поділена на кількість одиниць сукупності. Зважена – середня із варіантів, що повторюється не однакову кількість раз чи має різну статистичну вагу.
Середня квадратична використовується для оцінки варіації, тобто коли треба оцінити середню варіацію ознаки. Середнє гормонійне і середнє геометричне в даному випадку не знаходимо.
Середня арифметична проста:
= SХі / n
де Хі – індивідуальні значення ознаки;
n ‑ кількість одиниць сукпності.
Середня арифметична зважена. Оскільки сукупність згрупована, а частоти варіантів задані явно, то визначаємо середню арифметичну зважену величину:
;
де Хі – індивідуальні значення ознаки;
mі ‑ кількість однакових варіант.
Структурні середні характеризують структуру варіаціонних рядів. До них відносяться мода і медіана. Вони виражають визначене значення ознаки у ряду розподілу.
Мода – значення ознаки, що найбільш часто повторюється.
Медіаною називається значення ознаки, що знаходиться в середині ранжируємого ряду і поділяє цей ряд на дві рівні частини
Структурні середні
а) визначення моди:
;
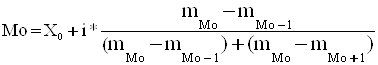де Х0 – нижня границя модального інтервалу;
і – величина інтервалу;
mMo ‑ відносна частота модального інтервалу;
mMo-1 ‑ відносна частота, передуючого модальному, інтервалу;
mMo+1 – відносна частота, наступного після модального, інтервалу.
б) визначення медіани:
де Х0 – нижня границя медіанного інтервалу;
і – величина інтервалу;
mі – загальна сума частот усіх інтервалів;
mе – частота медіанного інтервалу;
Sme-1 – сума частот до медіанного інтервалу.
Крім визначення середніх величин в цьому пункті курсової роботи знаходимо показники варіації. Вони показують коливність ознаки у сукупності. До них відносяться: розмах варіації, середньо лінійні відхилення, середньоквадратичні відхилення і дисперсія
Показники варіації:
а) середньоквадратичне відхилення - показує наскільки в середньому індивідуальне значення відхиляється від середнього, але з врахуванням знаку.
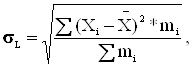
б) дисперсія
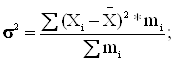
Відносні показники варіації(коефіцієнти варіації):
а) лінійний
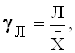
б) квадратичний
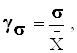
1) Проведемо розрахунок середніх показників та показників варіації за кількісною ознакою – час автомобіля у русі. Для цього нам необхідно використати структурне групування:
Середні показники:
= (43,49*5 + 45,56*4 +51,6*3 + 57,64*3 + 63,68*5)/20 = 52,29
Середній коефіцієнт часу у русі становить 52,29 год.
Модальним інтервалом є інтервал 36,5 – 42,54.
Мо = 36,5 + 6,04*
= 66,7
Найчастіше зустрічається такий час у русі як 66,7.
Медіанним інтервалом є інтервал 42,54 – 48,58.
Ме = 42,54 + 6,04*
= 50,09
50% автомобілів мають час у русі більший за 50,09год.,а 50% автомобілів – менше 50,09 год.
Показники варіації:
Rх = 66,7 – 36,5 = 30,2
Кількість показників часу у русі змінюються в межах 30,2
=7,3
В середньому індивідуальні значення кількісної ознаки – час у русі відхиляються від середнього значення на 7,3.
σ2 =6165,9 год.
σ = 
= 78,5 год.
Відхилення індивідуальних значень кількісної ознаки – час у русі від середнього значення в квадраті становить 78,5 год.
Квадратичне відхилення індивідуальних значень кількісної ознаки – час у русі від середнього значення становить 6165,9 год.
Коефіцієнти варіації:
Вважаючи, що якщо коефіцієнт варіації більше 30% то сукупність неоднорідна.
2) Проведемо ще один розрахунок середніх показників та показників варіації за кількісною ознакою – коефіцієнт використання вантажопідйомності. Дані беремо з таблиці структурного групування:
= ( 0,79 * 4 + 0,86 * 6 + 0,93 * 6 + 0,99 * 2 + 1,07 * 2) /20 = 0,98
Середній коефіцієнт використання вантажопідйомності становить 0,98.
Модальним інтервалом є інтервал 0,89 – 0,96.
Мо = 0,89 + 0,07*
= 0,89
Найчастіше зустрічається такий коефіцієнт використання вантажопідйомності 0,89.
Медіанним інтервалом є інтервал 0,82 – 0,89.
Ме = 0,82 + 0,07*
= 0,89
50% автомобілів мають коефіцієнт використання вантажопідйомності більший за 0,89, а 50% автомобілів – менше 0,89.
Показники варіації:
Rх = 1,11 – 0,75 = 0,36
Кількість показників коефіцієнту використання вантажопідйомності змінюються в межах 30,2.
= 0,1
В середньому індивідуальні значення кількісної ознаки – коефіцієнт використання вантажопідйомності відхиляються від середнього значення на 0,1
σ2 =0,2622.
σ = 
= 0,51 год.
Квадратичне відхилення індивідуальних значень кількісної ознаки – коефіцієнт використання вантажопідйомності від середнього значення становить 0,2622 як в одну так і в іншу сторону.
Відхилення індивідуальних значень коефіцієнт використання вантажопідйомності від середнього значення в квадраті становить 0,51.
Коефіцієнти варіації:
Вважаючи, що якщо коефіцієнт варіації менше 30% то сукупність однорідна.
3) Проведемо ще один розрахунок середніх показників та показників варіації за кількісною ознакою – обсяг перевезень. Дані беремо з таблиці структурного групування:
= ( 546,1 * 5 + 598,3 * 6 + 650,5 * 1 + 702,7 * 4 + 754,9 * 4) /20 = 640,06
Середній обсяг перевезень становить 640,06.
Модальним інтервалом є інтервал 624,4 – 676,6.
Мо = 624,4 + 52,2*
= 657,03
Найчастіше зустрічається такий обсяг перевезень 657,03.
Медіанним інтервалом є інтервал 520 – 572,2.
Ме = 520 + 52,2*
= 563,5
50% автомобілів мають обсяг перевезень більший за 563,5, а 50% автомобілів – менше 563,5. Показники варіації:
Rх = 781 - 520 = 261
Кількість показників коефіцієнту використання вантажопідйомності змінюються в межах 30,2.
= 72,04
В середньому індивідуальні значення кількісної ознаки – обсяг перевезень відхиляються від середнього значення на 72,04.
σ2 =6599,56.
σ = 
= 81,24.
Квадратичне відхилення індивідуальних значень кількісної ознаки – обсяг перевезень від середнього значення становить 6599,56 як в одну так і в іншу сторону.
Відхилення індивідуальних значень обсяг перевезень від середнього значення в квадраті становить 81,24.
Коефіцієнти варіації:
Вважаючи, що якщо коефіцієнт варіації менше 30% то сукупність однорідна.
Похожие работы
... і становив 2.30, відповідно збільшився дохід, прибуток і рентабельність перевезень що призвело до зменшення витрат підприємства. 3. Технологія і організація перевезень фанери з міста Рівне (Україна) в місто Мілан (Італія) рухомим складом ТзОВ „Камаз-Транс-Сервіс” 3.1 Дослідження вантажопотоку Згідно договору, укладеного ТзОВ „Камаз-Транс-Сервіс”, на 2006 рік прогнозується обсяг перевезень ...
... екстенсивного й інтенсивного використання основних виробничих фондів підприємства: (2.7) Результати розрахунків зведемо в таблицю 2.3. Найважливішим показником, що характеризує ефективність використання основних виробничих фондів підприємства, служить показник фондовіддачі, тобто обсяг виробленої продукції у вартісному чи натуральному вираженні, який приходиться на 1 грн. середньорічної ...
... задовольняє замовників. Перш за все, автомобілі підприємства застарілі, по-друге, продуктивність їх настільки мала, що їх просто недоцільно використовувати, та вони і не відповідають типу і виду вантажу. 3. Перевезення цементу автомобільним транспортом ЗАТ «УБ РАЕС» 3.1 Організація перевезень цементу на підприємстві Перевезення вантажів автомобільним транспортом на підприємстві ЗАТ « ...
... зріс на 3,16%; у 2005 р. в ТОВ «СПП ЛАНА» були надзвичайні доходи – 47 тис. грн.; чистий прибуток в ТОВ «СПП ЛАНА» зріс на 6,32%. 3. ШЛЯХИ ЕФЕКТИВНОГО ВИКОРИСТАННЯ ПРИБУТКУ НА ПІДПРИЄМСТВІ 3.1 Прогнозування прибутку підприємства на основі методів екстраполяції При аналізі ефективного використання прибутку підприємства важливе значення мають методи його прогнозування. Більшість методів ...
0 комментариев