Навигация
Факторные модели
2.5.3 Факторные модели
Под факторной моделью будим понимать аналитическую макромодель, сформированную по результатам измерения параметров РЭ в процессе реализации активного факторного эксперимента. Каждый параметр в этом случае может быть выражен полиноминально
|
или мультипликативно
|
где
Gi - аттестуемый параметр;
pi - постоянная факторного уравнения;
gij - парциальное факторное уравнение, представляющее аналитическую
зависимость от j фактора;
xj – фактор представляющий функцию gij.
Таким способом могут быть аттестованы как статические параметры, например в виде вольт-амперных характеристик (ВАХ), так и динамические параметры, например в виде Y-параметров. В первую очередь факторное пространство определяет частотный диапазон, режим электропитания по постоянному току и температура. Могут быть добавлены и другие факторы, способные влиять на значение параметров модели.
В общем виде факторная модель может быть выражена двумя уравнениями. Уравнение ВАХ
I=I(X) (2.17)
и уравнением
Y=Y(w,X) (2.18)
где I – вектор токов, определяющих рабочую точку;
Х – вектор факторов за исключением частоты;
Y – матрица проводимостей;
w - угловая частота.
Каждую из вещественных составляющих уравнений (2.17) и (2.18) определяют в виде аналитических зависимостей (2.15) или (2.16).
Факторная модель наиболее полно отвечает аналитическим макромоделям, описание которых приведено в п. 2.5.2. Измерение статических и физических параметров факторных моделей может быть автоматизировано при использовании способа по АС СССР № 1317370 /3/ устройств по АС СССР №1084709 /5/. Способ /3/ и устройства /6,7/ не имеет принципиальных отличий по частотному диапазону и могут быть применены в СВЧ диапазоне. Использование этих устройств при применениях к СВЧ имеет определенные преимущества, т.к. для реализации основных измерительных операций не обязательно применение согласованного волнового тракта. Однако и в этом случае при конструировании измерительных цепей, которые содержат ИГ необходимо учитывать специфику цепей СВЧ диапазона.
Информация, представленная уравнениями (2.17) и (2.18) в принципе достаточна для описания макромоделей, приведенных в /8/. Например, для идентификации модели Эберса-Молла нужно расширить систему (2.17) и (2.18) добавив данные об инверсном режиме включения транзистора. При этом уравнение (2.18) используется для определения нелинейных зависимостей емкостей переходов транзистора.
3 Тестер для измерения параметров радиоэлектронных элементов
3.1 Методика измерения
3.1.1 Измерение статических параметров
В интегрированных САПР для расчета транзисторных схем в режиме большого сигнала, как правило, используют модели Эберса-Молла или Гуммеля-Пуна, основанные на суперпозиции прямого и инверсного включения транзистора /2,10/. В этом случае неизбежны искажения моделируемых вольтамперных характеристик (ВАХ), так как в основе их описания заложены свойства идеального p-n перехода, смещенного в прямом или обратном направлении.
В этой связи классическое определение ВАХ связанное с непосредственным измерением токов и напряжений на входных и выходных электродах транзистора имеет принципиальное значение как для корректировки указанных выше моделей, так и для изучения тонкой структуры процессов в транзисторе /11-13/.
В процессе планирования эксперимента при моделировании радиоэлементов важную роль имеет выбор непосредственно измеряемой системы параметров с точки зрения совместимости с требованиями к определяемой модели, методам и техническим средствам измерения в первую очередь должны быть реализованы два главных условия, во-первых, сокращение времени и материальных затрат на этапе сбора и обработки первичной информации, во-вторых, широкое использование алгоритмических методов измерения, позволяющих при реализации простых методов измерения получить сложные модели путем глубокой математической обработки информации.
Измерение ВАХ транзистора можно комплексно автоматизировать использовав методику измерения по А.С. СССР №1084709 /13/. При этом предоставляется возможным в процессе измерения ВАХ так же определять данные, достаточные для вычисления Y-параметров транзистора в каждой из точек спектра плана эксперимента, который реализуется в процессе измерения ВАХ. При этом аттестируется система ВАХ
|
Uб=Uб(Ik,Uk),
где Iб и Uб – ток и напряжения базы транзистора соответственно;
Ik и Uk – ток и напряжение его коллектора.
При расчетах электронных устройств система практически не используется, однако при определении ее параметров относительно просто автоматизировать измерительный процесс и совместить определение статистических и динамических параметров на одной технологической установке 15.Расширяя факторные пространства в температурную область из системы (3.1) получаем систему
Iб= Iб(Iк,Uк,To); (3.2)
Uб= Uб(Iк,Uк,To), (3.3)
где To– температура.
На практике наиболее широко используют ВАХ соответствующие системам Н-параметров (параметры ВАХ ток Iб и напряжение Uк) или Y-параметров (аргументы ВАХ напряжения Uб и Uк), т.е. системы
Iк = Iк (Iб,Uк); (3.4)
Uб = Uб(Iб,Uк), (3.5)
Iк = Iк (Uб,Uк); (3.6)
Iб = Iб(Uб,Uк). (3.7)
Если базовая система (3.1) соответствует полиминальной модели, то ее факторные функции (ФФ) имеют вид /5,14/Iб = k1 + Iб (Iк) +Iб(Uк); (3.8)
Uб =k2 + Uб(Iк) + Uб (Uк), (3.9)
где k1 и k2 – постоянные факторных функций (ПФФ), а индексы 1 и 2 указывают на различие этих коэффициентов в первом и втором уравнениях системы; Iб (Iк), Iб(Uк), Uб(Iк), Uб (Uк) - аналитические функции, представляющие собой элементарные факторные функции (ЭФФ).
Iк = k1 + Iк (Iб) +Iк(Uк); (3.10)
Uб =k2 + Uб(Iб) + Uб (Uк) (3.11)
Iк = k1 + Iк (Iб) +Iк(Uк); (3.12)
Iб =k2 + Iб(Uб) + Uб (Uк). (3.13)
Преобразования параметров ФФ (3.8)-(3.9) в ФФ (3.10)-(3.11) или (3.13)-(3.14) было предложено производить по табличным значениям ЭФФ системы (3.8)-(3.9).
Определение ЭФФ Iк (Iб) и Uк (Uб) не представляет сложности, так как они представляют собой обратные функции ЭФФ Iб (Iк) и Uб (Uк). Для определения ЭФФ Uб (Iб) можно использовать ЭФФ Uб (Iк) в которую нужно подставить табличные значения ЭФФ Iк (Iб). Таким же способом по ЭФФ Uб (Uк) и Iк (Iб) находим ЭФФ Iк (Uб(Uк)) и на последнем этапе ЭФФ Iб (Uб) определяем через ЭФФ Iб (Iк) и Iк (Uб), т.е. в виде Iб (Iк(Uб)).
Аналитически ЭФФ определены числовым методом трем их табличным значениям.
Каждая из ЭФФ отвечает одному из уравнений, приведенных в таблице 3.1
Таблица 3.1 - Структура ЭФФ| Код | Структура |
| 1 | f1=ax2+bx+c |
| 2 | f2=ln(f1) |
| 3 | f3=exp(f1) |
| 4 | f4=a/(x+b)+c |
| 5 | f5=a; b=c=0 |
Блок схема алгоритма формирования ЭФФ приведена на рисунке 1
Система Системы Система
(10)-(11) (8)-(9) (12)-(13)
![]()
![]()
![]()
![]()
![]()
![]() Iк(Iб)
Iб(Uк) Iб(Uк)
Iк(Iб)
Iб(Uк) Iб(Uк)
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]() Iк(Uк) Iк(Iб) Iб(Iк)
Iб(Iк(Iб)) Iб(Uб)
Iк(Uк) Iк(Iб) Iб(Iк)
Iб(Iк(Iб)) Iб(Uб)
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]() Uб(Iб) Uб(Iк(Iб)) Uб(Iк) Iк(Iб) Iб(Uб)
Uб(Iб) Uб(Iк(Iб)) Uб(Iк) Iк(Iб) Iб(Uб)
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]() Iб(Uк) Uб(Uк) Iк(Uб(Uк)) Iк(Uк)
Iб(Uк) Uб(Uк) Iк(Uб(Uк)) Iк(Uк)
![]()
![]() Рисунок 1 - Алгоритм преобразования систем ЭФФ
Рисунок 1 - Алгоритм преобразования систем ЭФФ
В результате реализации алгоритма, рисунок 1, находятся ЭФФ преобразованных ВАХ, чтобы определить ФФ этих ВАХ необходимо вычислить соответствующие ПФФ, которые можно вычислить по табличным значениям ФФ. Исходными данными для расчета являются табличные значения ЭФФ.
Рассмотрим алгоритм формирования табличных значений ФФ для плана 34-2. Пусть fij – элементы ЭФФ, где i=1,4 – индекс фактора, а j=1,3 – индекс уровня фактора. Если принять, что при i=1 фактор изменяется по строкам матрицы планирования (МП), i=2 – по столбцам, i=3 – по диагонали справа-налево и i=4 – по диагонали слева-направо, то обозначив символом ykl элементы МП, где k=1,3 и l=1,3 получим условия для определения системы уравнений, достаточных для определения элементов ykl по известным элементам fij.
Из теории планирования эксперимента известно, что утроенные значения fkl равны сумме элементов yijпо фиксированному уровню фактора i.
Тогда для полиминальной модели исходные системы уравнений имеют вид для первого фактора
3f11=y11+y12+y13; 3f21=y21+y22+y23; 3f23=y31+y32+y33, (3.14)
для второго фактора
3f21=y11+y21+y31; 3f22=y12+y22+y32; 3f23=y13+y23+y33, (3.15)
для третьего фактора
3f31=y11+y22+y33; 3f32=y12+y23+y13; y33=y13+y21+y32, (3.16)
и для четвертого фактора
3f41=y31+y22+y13; y42=y11+y23+y32; y21=y12+y33. (3.17)
Алгоритм определения преобразованной МП по табличным значениям ЭФФ сводится к вычислению этих yij этой МП по формулам, полученным в результате совместного решения систем (3.14)-(3.17):
y31=f41 + f21 + f32 - f11 - f12; (3.18)
y32=f33 + f42 + f22 - f11 - f12; (3.19)
y21=f33 + f21 + f24 - f11 - f13; (3.20)
y13=3f33 - y21 - y32; (3.21)
y12=3f22 - 3f41 - y32 + y13 + y31; (3.22)
y23=3f32 – y12 - y31; (3.23)
y11=3f11 – y12 – y13; (3.24)
y22=3f12 - y21 - y32; (3.25)
y33=3f13 – y31 - y32. (3.26)
При полиминальной модели (ФФ представляет собой произведение ЭФФ) также используют формулы (3.18)-(3.26), но для логарифмированных табличных значений ФФ.
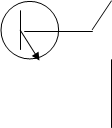
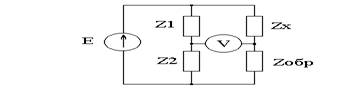
Для аттестации параметров модели Эберса-Молла необходимо определить уравнения (2.18) для инверсного включения транзистора. Дополнительные данные для определения этой модели или ее корректировки могут быть получены при определении переходов база-эммитер и база-коллектор согласно схемам, рисунки 3.2 и 3.3.
![]()
![]()
 | |||
![]()
![]()
 | |||
![]()
![]()
Рисунок 3.2 - Измерение ВАХ в нормальном режиме
|
 | |||
|
|
|
|
|
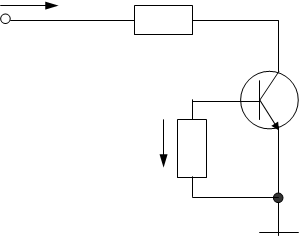
Рисунок 3.3 - Измерение ВАХ в инверсном режиме.
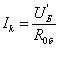 |
Регистрируются напряжения Uк, Uб, которые падают на образцовых резисторах R0k, R0б. Соответственно токи Iк, Iб рассчитываются по формулам.
|
|
Ток Ik служит для контроля режима измерения, если электропитание проводится от источника тока.
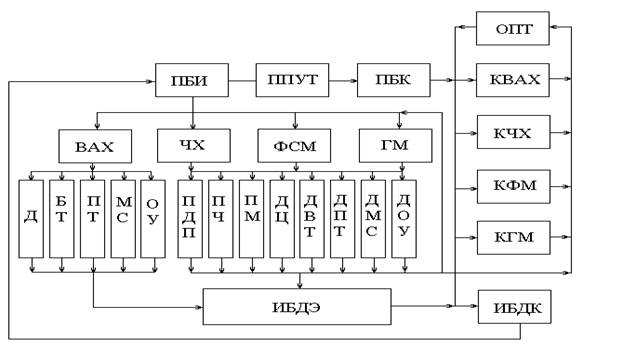
В процессе реализации измерительного процесса необходимо руководствоваться сведениями о структуре РЭ, приведенными в п. 2.2-2.3.
Похожие работы
... плана ФЭ. Большое разнообразие моделей РК приводит к необходимости использования разнообразных способов и технических средств для измерения их параметров. Как правило, статические и динамические параметры РК измеряют на разных технологических установках. Методы построения средств измерения для идентификации моделей РК могут быть сведены к следующим принципам, учитывающим особенности подключения ...
... может быть определена в результате решения матричного уравнения Y = 2(K - Ko ) , (16) где -1 - знак обращения матриц К и Ко. 3.4 Методика измерения двух- и четырехполюсных радиоэлементов Для случая двухполюсника n = 1 (17) имеем i = 1; j = 0. (18) Очевидно, что при условиях (17) - (18) имеем: 1) коэффициенты матриц Ко и К с ...
... : ¾ температура, °С +25±10; ¾ относительная влажность воздуха, % 45...80; ¾ атмосферное давление, мм рт. ст. 630...800. Так как блок интерфейсных адаптеров предназначен для работы в нормальных условиях, в качестве номинальных значений климатических факторов указанные выше принимают нормальные значения ...
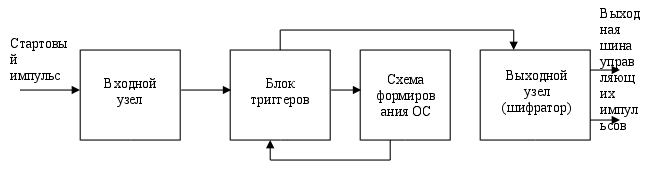
... в народном хозяйстве. Специальная часть. 3. 1. Определение задачи. Из задания на курсовое проектирование определим суть задачи: для некоторого синхронного цифрового автомата необходимо спроектировать устройство управления на основе жёсткой логики, которое в соответствии с заданными кодами микрокоманд формирует на выходной десятиразрядной шине управляющую последовательность цифровых сигналов. 3. ...
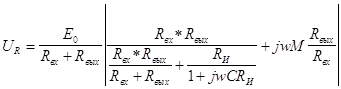


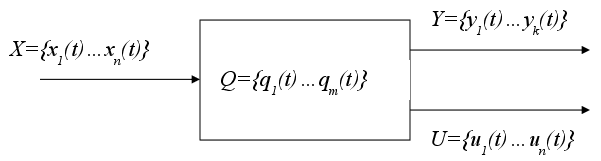
0 комментариев