Навигация
Численные методы вычисления интегралов
Численные методы вычисления интегралов. Метод Ньютона-Котеса. Метод Гаусса
1. Численные методы вычисления интегралов. Постановка задачи
Решая физические задачи, часто приходится вычислять значения определённых интегралов от функций ![]() . Во многих случаях, в виду того, что подлежащий вычислению интеграл не выражается через элементарные функции, прибегают к приближённым численным методам.
. Во многих случаях, в виду того, что подлежащий вычислению интеграл не выражается через элементарные функции, прибегают к приближённым численным методам.
Прежде всего, рассмотрим случай, когда ![]() - конечный интервал.
- конечный интервал.
В таком случае, как известно, функция ![]() является ограниченной, т.е.
является ограниченной, т.е. ![]() . В этом случае наиболее часто применяемый численный метод интегрирования состоит в том, что интеграл от
. В этом случае наиболее часто применяемый численный метод интегрирования состоит в том, что интеграл от ![]() заменяется некоторой линейной комбинацией значений
заменяется некоторой линейной комбинацией значений ![]() в
в ![]() точках
точках ![]() :
:
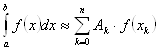 (1)
(1)
Формула (1) называется квадратурной формулой, а коэффициенты ![]() - квадратурными коэффициентами или весами, абсциссы
- квадратурными коэффициентами или весами, абсциссы ![]() - узлами квадратурной формулы.
- узлами квадратурной формулы.
Методы численного интегрирования классифицируются в зависимости от того, заданы ли значения аргумента через равные промежутки или нет. Так методы Ньютона-Котеса требуют, чтобы значения ![]() были заданы с постоянным шагом, а методы Гаусса не налагают такого ограничения. Перейдём к рассмотрению этих методов.
были заданы с постоянным шагом, а методы Гаусса не налагают такого ограничения. Перейдём к рассмотрению этих методов.
2. Методы Ньютона-Котеса
Пусть ![]() различные точки отрезка
различные точки отрезка ![]() , служащие узлами интерполяции для некоторой интерполирующей функцию
, служащие узлами интерполяции для некоторой интерполирующей функцию ![]() функции
функции ![]() . Тогда имеем:
. Тогда имеем:
![]() (2)
(2)
где ![]() - остаточный член. Предположим, что
- остаточный член. Предположим, что
![]() (3)
(3)
причём ![]() подобраны так, чтобы все интегралы
подобраны так, чтобы все интегралы
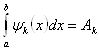 (4)
(4)
можно вычислить точно. Тогда мы получаем квадратурную формулу
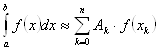 (5)
(5)
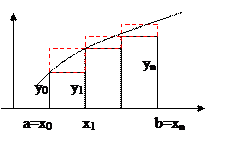
2.1 Формула трапеций
|
|

Рис. 1.
а) графический вывод:
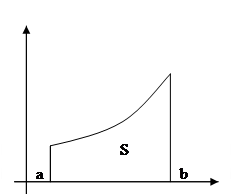
Определённый интеграл 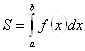 , как известно, задаёт площадь
, как известно, задаёт площадь ![]() криволинейной трапеции
криволинейной трапеции ![]() , поэтому, вписав ломаную в дугу кривой
, поэтому, вписав ломаную в дугу кривой ![]() , мы получаем, что площадь криволинейной трапеции можно приближённо вычислить как сумму площадей трапеций:
, мы получаем, что площадь криволинейной трапеции можно приближённо вычислить как сумму площадей трапеций:
![]() (6)
(6)
Между тем, очевидно, что
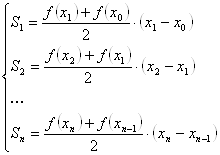 (7)
(7)
Так как, в методах Ньютона-Котеса, ![]() , учитывая (6) получаем:
, учитывая (6) получаем:
![]() (8)
(8)
или, соединяя подобные члены, имеем:
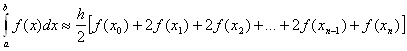 (9)
(9)
Формула (9) – называется формулой трапеций.
б) Аналитический вывод:
Выведем формулу трапеции аналитическим способом. Для этого используем интерполяционный многочлен Лагранжа для отрезка ![]() , построим многочлен первой степени, который на концах отрезка принимает заданные значения
, построим многочлен первой степени, который на концах отрезка принимает заданные значения ![]() . Ясно, что в таком случае интерполирующая функция
. Ясно, что в таком случае интерполирующая функция ![]() имеет вид:
имеет вид:
![]() (10)
(10)
т.к. в методе Ньютона-Котеса ![]() , учитывая (3) и (4), из (10) получаем:
, учитывая (3) и (4), из (10) получаем:
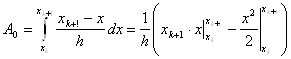
![]() (11)
(11)
Аналогично, 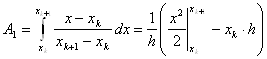 , т.е.
, т.е.
![]() (12)
(12)
Таким образом, получаем формулу:
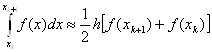 (13)
(13)
тогда, используя свойство аддитивности оператора интегрирования, имеем:
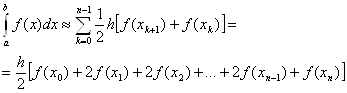 (14)
(14)
где ![]() . Получили формулу (14) трапеций, которая естественно, совпадает с (9).
. Получили формулу (14) трапеций, которая естественно, совпадает с (9).
Похожие работы
... отклонения Гаусса (10) по норме индуцированной скалярным произведением (15), действительно: (18) а дискретная норма Гаусса невязки имеет вид: (19) 2.2 Интегральное приближение функции заданной аналитически В предыдущем параграфе мы рассматривали приближение функции методом наименьших квадратов, предполагая, что значения функции заданы таблично, поэтому мы ...
... Впрочем, для наиболее распространённых псевдослучайных чисел период столь велик, что превосходит любые практические потребности. Подавляющее большинство расчётов по методу Монте-Карло осуществляется с использованием псевдослучайных чисел. Значения любой случайной величины можно получить путём преобразования значений одной какой-либо случайной величины. Обычно роль такой случайной величины играет ...
... такое определённый интеграл. Возможны два различных подхода к определению определённого интеграла. ОПРЕДЕЛЕНИЕ 1: приращение F(b)-F(a) любой из преобразованных функций F(x)+c при изменении аргумента от x=a до x=b называют определённым интегралом от a до b функции f и обозначается . Причём функция F является первообразной для функции f на некотором промежутке D, а числа а и b принадлежат этому ...
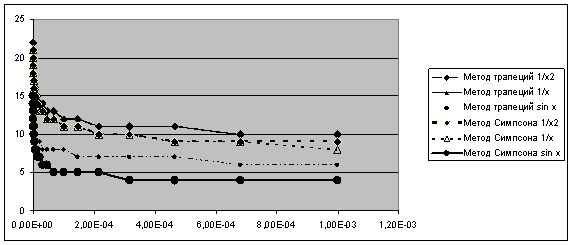
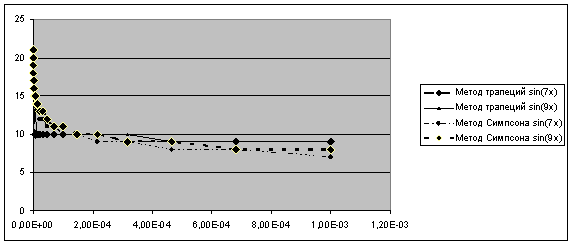
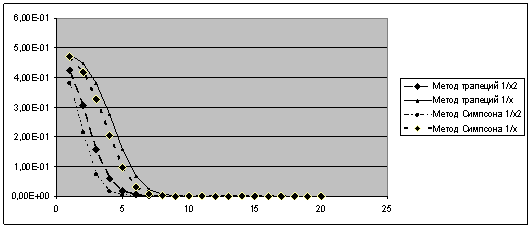
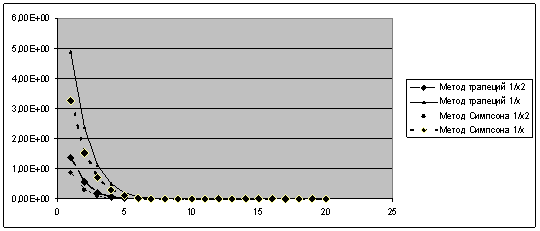
... и методика испытаний 5.1 Объект испытаний Объектом испытаний является программа, предназначенная для исследования внутренней сходимости численного интегрирования с помощью методов вычисления интегралов: методы трапеций и Симпсона. 5.2 Цель испытаний Целью испытаний является проверка точности работы программы для данной задачи. 5.3 Требования к программе Во время испытаний ...
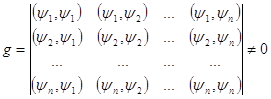
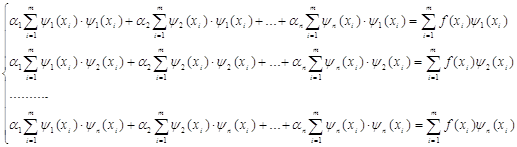


0 комментариев