Навигация
Эконометрический анализ выпуска рыбной продукции. Множественная регрессия и корреляция
2.1. Эконометрический анализ выпуска рыбной продукции. Множественная регрессия и корреляция.
Отбор факторов для построения множественной регрессии.
На любой экономический показатель чаще всего оказывает влияние не один, а несколько факторов. В данной работе будет исследоваться экономический процесс, в котором также учитывается влияние нескольких факторов на результат.
Для отбора факторов используется наиболее распространённый метод исключения, то есть из всего набора факторов происходит их отсев.
Факторы, включаемые во множественную регрессию, должны отвечать следующим требованиям:
· Они должны быть количественно измеримы.
· Факторы не должны быть интеркоррелированы и тем более находиться в точной функциональной связи.
Отбор факторов производится на основе качественного теоретико-экономического анализа. Однако теоретический анализ часто не позволяет однозначно ответить на вопрос о количественной взаимосвязи рассматриваемых признаков и целесообразности включения фактора в модель. Поэтому отбор факторов обычно осуществляется в две стадии: на первой подбираются факторы исходя из сущности проблемы; на второй - на основе матрицы показателей корреляции определяют t-статистики для параметров регрессии.
Данные, характеризующие рассматриваемую проблему, представлены в таблице. Статистические сведения приведены за 7 лет.
| 1999 | 2000 | 2001 | 2002 | 2003 | 2004 | 2005 | |
| y | 2201 | 1913 | 1384 | 1067 | 961 | 1172 | 918 |
| x1 | 736 | 730,5 | 719,7 | 740,1 | 748,6 | 744,9 | 745,9 |
| x2 | 10,8 | 10,7 | 10,6 | 10,3 | 10,1 | 9,8 | 9,5 |
| x3 | 148532 | 147501 | 146304 | 145649 | 144964 | 144168 | 143474 |
| x4 | 114,9 | 115 | 114,4 | 112,6 | 111,6 | 112,5 | 111,3 |
| x5 | 3167 | 3983,9 | 5325,8 | 6831 | 8900 | 10976,3 | 13667,8 |
| x6 | 5807,5 | 7305,6 | 8934,6 | 10830,5 | 13243,2 | 16966,4 | 21597,9 |
| x7 | 4901 | 4876 | 4795 | 4709 | 4602 | 4579 | 4457 |
| x8 | 0,7 | 0,4 | 0,4 | 0,6 | 0,7 | 1,4 | 1,5 |
| x9 | 23,7 | 29,7 | 36,7 | 36,1 | 43,2 | 61,6 | 78,4 |
| x10 | 65,7 | 65,34 | 65,23 | 65,95 | 64,85 | 65,27 | 65,3 |
где у - производство рыбной продукции (минтай, судак, камбала, сельдь, палтус и т.д.), тонны;
х1 – численность персонала, тыс. человек;
х2 – число предприятий отлова рыбы, тысяч;
х3 - численность населения, тыс. чел;
х4 – число предприятий на государственном обеспечении, тысяч;
х5 - денежные доходы, млрд руб;
х6 - ВВП, млрд руб;
х7 - правоохранительных организаций, тысяч;
х8 – страхование производственных фондов, %;
х9 - инвестирование в рыболовную промышленность, млрд руб;
х10 – увеличение стоимости квот на отлавливаемую рыбу, %.
Присутствие лишних факторов приводит только к статистической незначимости параметров регрессии. Естественно, использовать все факторы в уравнении регрессии не удастся, так как число наблюдений невелико, и получить значимые параметры уравнения регрессии при таком количестве факторов невозможно. Их число должно быть сведено к минимуму.
Так как в данной экономической модели уже выделены факторы, оказывающие влияние на результат, то при отборе факторов для построения множественной регрессии воспользуемся методом исключения. В данном случае отбор факторов основывается на вычислении матрицы парных коэффициентов корреляции.
Коэффициенты интеркорреляции (т.е. корреляции между объясняющими переменными) позволяют исключить из модели дублирующие факторы.
Для того чтобы сделать выводы о влиянии экономических факторов на развитие лесного хозяйства, необходимо на основе данных, представленных в работе за семилетний период (с 1998 по 2004 гг.), составить модель множественной регрессии, которая бы описывала зависимость производство лекарств от всех вышеперечисленных факторов. Должны быть решены вопросы, связанные с выбранными факторными признаками и с видом применяемого уравнения регрессии. Далее следует рассмотреть влияние выбранных факторов на результат при наличии временной переменной. Совокупность выполненных работ позволит сформулировать выводы о взаимосвязях в изучаемой области.
Частный коэффициент корреляции отражает чистое влияние рассматриваемого фактора на результат, т.к. остальные факторы закрепляются на определенном уровне, т.е. являются постоянными.
Формула для расчета частного коэффициента корреляции, измеряющего влияние на у фактора хi при неизменном уровне других факторов, можно определить по формуле:
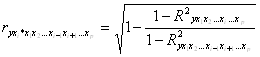 ,
,
где ![]() - множественный коэффициент детерминации всего комплекса р факторов с результатом;
- множественный коэффициент детерминации всего комплекса р факторов с результатом;
![]() - тот же показатель детерминации, но без введения в модель фактора xi.
- тот же показатель детерминации, но без введения в модель фактора xi.
Парные коэффициенты корреляции вычисляются по формуле:
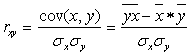
Получили следующую таблицу коэффициентов корреляции:
|
| у | х1 | х2 | х3 | х4 | х5 | х6 | х7 | х8 | х9 | х10 |
| у | 1 | ||||||||||
| х1 | -0,883 | 1 | |||||||||
| х2 | -0,521 | 0,1002 | 1 | ||||||||
| х3 | -0,495 | 0,0697 | 0,959 | 1 | |||||||
| х4 | 0,4136 | 0,035 | -0,755 | -0,8104 | 1 | ||||||
| х5 | 0,4561 | -0,003 | -0,970 | -0,9792 | 0,8554 | 1 | |||||
| х6 | 0,3665 | 0,0675 | -0,975 | -0,9398 | 0,7412 | 0,9741 | 1 | ||||
| х7 | -0,007 | 0,1411 | -0,526 | -0,3517 | -0,045 | 0,4114 | 0,6033 | 1 | |||
| х8 | 0,595 | -0,342 | -0,694 | -0,7302 | 0,5306 | 0,6198 | 0,545 | 0,0165 | 1 | ||
| х9 | -0,135 | 0,4521 | -0,333 | -0,2732 | 0,6315 | 0,4497 | 0,4456 | 0,1575 | -0,239 | 1 | |
| х10 | -0,635 | 0,2972 | 0,7292 | 0,70582 | -0,765 | -0,6855 | -0,5901 | 0,0468 | -0,865 | -0,188 | 1 |
Значения коэффициентов корреляции, находящиеся в диапазоне 0< ׀r׀≤ 0.3 говорят о слабой связи между наблюдаемыми признаками; значения 0.3≤ ׀r׀≤ 0.7 – о средней связи и 0.7≤׀r׀< 1 – о тесной связи. Положительные значения коэффициентов корреляции свидетельствуют о прямой связи между переменными, отрицательные – об обратной связи, то есть увеличение одного из факторов сопровождается уменьшением другого. Из полученной матрицы коэффициентов парной корреляции следует, что ряд факторов имеет парные коэффициенты корреляции больше 0,7.
|
| у | х1 | х2 | х3 | х4 | х5 | х6 | х7 | х8 | х9 | х10 |
| у | 1 | ||||||||||
| х1 | -0,883 | 1 | |||||||||
| х2 | -0,522 | 0,1 | 1 | ||||||||
| х3 | -0,495 | 0,07 | 0,959 | 1 | |||||||
| х4 | 0,414 | 0,035 | -0,756 | -0,81 | 1 | ||||||
| х5 | 0,456 | -0,003 | -0,971 | -0,979 | 0,855 | 1 | |||||
| х6 | 0,366 | 0,067 | -0,975 | -0,94 | 0,741 | 0,974 | 1 | ||||
| х7 | -0,007 | 0,141 | -0,527 | -0,352 | -0,046 | 0,411 | 0,603 | 1 | |||
| х8 | 0,595 | -0,342 | -0,694 | -0,73 | 0,531 | 0,62 | 0,545 | 0,016 | 1 | ||
| х9 | -0,135 | 0,452 | -0,334 | -0,273 | 0,632 | 0,45 | 0,446 | 0,158 | 0,113 | 1 | |
| х10 | -0,635 | 0,297 | 0,729 | 0,706 | -0,765 | -0,69 | -0,59 | 0,047 | -0,673 | -0,189 | 1 |
Из пары факторов х3 и х2 исключаем фактор х2, так как его связь с другими факторами более сильная, чем связь x3 с ними. Исключаем фактор x7, так как его связь с y очень незначительная. По такой схеме исключаем все другие факторы. Таким образом, для построения модели остаются факторы х1, х5, х8 и х10. Матрица коэффициентов парной корреляции для них выглядит следующим образом:
|
| у | х1 | х5 | х8 | х10 |
| у | 1 | ||||
| х1 | -0,88300608 | 1 | |||
| х5 | 0,45605173 | -0,003474 | 1 | ||
| х8 | 0,59499201 | -0,342415 | 0,619844 | 1 | |
| х10 | -0,635065 | 0,297207 | -0,685489 | -0,6729266 | 1 |
Для получения адекватной модели необходимо устранить мультиколлинеарность, т.е. вывести из рассмотрения факторы, которые имеют совокупное воздействие друг на друга. Наличие мультиколлинеарности факторов может означать, что некоторые из них всегда будут действовать в унисон. Для оценки мультиколлинеарности факторов может использоваться определитель матрицы парных коэффициентов корреляции между факторами. Чем ближе к нулю этот проеделитель, тем сильнее мультиколлинеарность факторов. Для наших парных коэффициентов корреляции между факторами матрица имеет вид:

![]()
Определитель матрицы парных коэффициентов корреляции между факторами равен 0,2, что достаточно близко к 0, следовательно, между оставшимися факторами наблюдается мультиколлинеарность.
Продолжим удаление факторов, являющихся самыми неинформативными, регулярно сопоставляя значения множественного коэффициента корреляции и детерминации (который оценивает качество построенной модели в целом) и проверяя значимость уравнения регрессии.
В следующих таблицах представлены результаты регрессионного анализа после исключения факторов х1, х5, х8, х10.
| ВЫВОД ИТОГОВ | |
| Регрессионная статистика | |
| Множественный R | 0,999530603 |
| R-квадрат | 0,999061427 |
| Нормированный R-квадрат | 0,995307133 |
| Стандартная ошибка | 29,05134237 |
| Наблюдения | 6 |
| Дисперсионный анализ | |||||
|
| df | SS | MS | F | Значимость F |
| Регрессия | 4 | 898372,4 | 224593,0982 | 266,111717 | 0,045939839 |
| Остаток | 1 | 843,9805 | 843,9804935 | ||
| Итого | 5 | 899216,4 |
|
| Коэффициенты | Стандартная ошибка | t-статистика | P-Значение |
| Y-пересечение | 30538,08691 | 1623,46624 | 18,81042319 | 0,03381216 |
| x1 | -26,94728304 | 1,07745261 | -25,01017937 | 0,02544087 |
| x5 | 0,007316604 | 0,00087595 | 8,352752758 | 0,07585572 |
| x8 | -242,9957642 | 101,983594 | -2,382694665 | 0,25297163 |
| x10 | -81,66075105 | 21,2523898 | -3,842426757 | 0,16208611 |
По данным вычислениям уравнение регрессии будет иметь вид:
ŷ =30538,09-26,95*x1+0,007*x5-242.996*x8-81,66*x10.
б) Оценка практической значимости и надежности полученного уравнения.
Для оценки значимости параметров уравнения используется t- критерий Стьюдента. С помощью t-критерия Стьюдента для каждого из оставшихся факторов можно выяснить, формируется ли он под воздействием случайных величин (является ли фактор информативным).
Его можно определить как:
![]() ,
,
где ![]() - частный F- критерий Фишера, который определяется по формуле:
- частный F- критерий Фишера, который определяется по формуле:
 ,
,
где ![]() - множественный коэффициент детерминации всего комплекса р факторов с результатом;
- множественный коэффициент детерминации всего комплекса р факторов с результатом;
![]() - тот же показатель детерминации, но без введения в модель фактора xi.
- тот же показатель детерминации, но без введения в модель фактора xi.
n- число наблюдений;
m- число параметров в модели (без свободного члена).
При этом определяются две гипотезы:
Н0 - коэффициент статистически незначим;
Н1 - коэффициент статистически значим.
Затем сравнивается факторное значение t- критерия, т.е. вычисленное, и табличное, определенное по специальной таблице t-критерия. Если факторное значение окажется больше табличного, то гипотеза Н0 отклоняется и коэффициент признается статистически значимым.
В полученном уравнении tтабл: n-m-1=7-4-1=2, tтабл =4,3
Следовательно коэффициенты при факторах х1, х5 являются статистически значимыми, для них значение t-критерия больше 4,3, следовательно, можно сделать вывод о существенности данных параметров, которые формируются под воздействием неслучайных причин, а коэффициенты при х8, х10, соответственно, незначимы.
P-значение характеризует вероятность случайного характера формирования параметра. Из рассчитанных значений видно, что наибольшей вероятностью случайной природы факторов обладают b8 , поэтому этот фактор можно исключить из уравнения регрессии. Также удаляем фактор b10 (так как он не является значимым).
Проведём анализ данных для оставшихся двух факторов:
| ВЫВОД ИТОГОВ | |
| Регрессионная статистика | |
| Множественный R | 0,99242 |
| R-квадрат | 0,984897 |
| Нормированный R-квадрат | 0,974828 |
| Стандартная ошибка | 67,28282 |
| Наблюдения | 6 |
Дисперсионный анализ | |||||
|
| df | SS | MS | F | Значимость F |
| Регрессия | 2 | 885635,4 | 442817,7 | 97,8175049 | 0,001856086 |
| Остаток | 3 | 13580,93 | 4526,978 | ||
| Итого | 5 | 899216,4 | |||
|
| Коэффициенты | Стандартная ошибка | t-статистика | P-Значение |
| Y-пересечение | 287,2650033 | 1821,254 | 14,04644 | 0,00078146 |
| x1 | 2,866255447 | 2,231529 | -12,4227 | 0,00112406 |
| x5 | -0,145583563 | 0,001402 | 6,384305 | 0,00778112 |
Проверим еще раз наличие мультиколлинеарности оставшихся факторов. Для парных коэффициентов корреляции между факторами х1, х5 матрица имеет вид:
![]()
![]()
Определитель матрицы парных коэффициентов корреляции между факторами приближенно равен 1 что говорит об отсутствии мультиколлинеарности между оставшимися факторами.
Теперь из модели исключены явно коррелированные факторы, следовательно, можно приступать к оценке модели множественной регрессии. Значимость и надежность всего уравнения в целом определяется с помощью
F- критерия Фишера:
![]() ,
,
где R2- коэффициент (индекс) множественной детерминации;
n- число наблюдений;
m- число параметров при переменных х.
После вычисления F-критерия факторное значение сравнивается с табличным. Если факторное значение больше табличного, то уравнение статистически значимо и надежно.
Полученное уравнение ŷ = 287,265 +2,86*х1 -0,145*х5 является надежным и статистически значимым, т.к. Fфакт = 97,82 > Fтабл=6,94 (для определения Fтабл m=2, n-m-1=7-2-1=4).
Итак, окончательная математическая модель будет выглядеть следующим образом:
ŷ = 287,265 +2,86*х1 -0,145*х5.
Из полученного уравнения видно, что на производство рыбной продукции, тыс. тонн (фактор у) в большей степени влияют такие факторы как численность населения, на тыс. человек (фактор х1) и денежные доходы, млн. руб. (фактор х5). Причем при увеличении численности населения на тыс. человек на единицу производство рыбной продукции увеличится на 2,86 тонн, а при увеличении денежных доходов на 1 млрд руб. – уменьшится на 0,009 тонн.
Похожие работы
... № 270 “О плане счетов бухгалтерского учета”, в котором был представлен порядок отражения лизинга в бухгалтерском учете. Развитие сети коммерческих банков способствовало внедрению лизинговых операций в банковскую практику. Российские лизинговые компании начали образовываться с середины 2000 года. В октябре 2004 года была создана Российская ассоциация лизинговых компаний “Рослизинг”. В 2004 году “ ...
... выявляют, и, по соглашению с заказчиком, копируют или излагают информацию (в случае необходимости с соответствующей верификацией) об интересующих заказчика лицах. В частности, в фондах Российского Государственного Исторического архива можно обнаружить следующие документы персонального характера: 1. Послужные списки лиц состоявших на государственной службе (за исключением самых нижних чинов, ...
... ассортимент кулинарных изделий из рыбы, их повсеместное производство у нас в стране остаётся проблематичным, это связано с нехваткой или отсутствием современных производственных мощностей. 1.4. Факторы, влияющие на формирование ассортимента рыбной кулинарии Различают общие и специфичные факторы формирования ассортимента. Общими факторами, влияющими на формирование промышленного и ...
... цены на консервную продукцию снизились за год? Это связано с тем, что руководство намерено снизило их для того, чтобы реализовать продукцию. 3 Управление себестоимостью продукции на примере ОАО «Владивостокский рыбокомбинат» 3.1 Управление себестоимостью на основе утвержденного плана выпуска продукции ОАО «Владивостокский рыбокомбинат» создал и запустил консервный цех в ...
0 комментариев