Навигация
Доработки магистральной модели
3.2. Доработки магистральной модели
Неймановский луч, определяемый по формуле ![]() ,
,
выглядит на графике следующим образом.
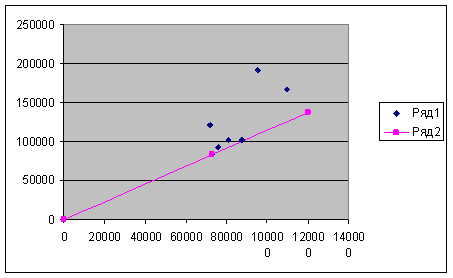
Как видно из графика, Неймановский луч, определяемый как луч с наименьшим тангенсом угла, соответствует всего двум точкам, характеризующим равновесию производственных затрат и валового выпуска во времени. Это говорит о том, что существует возможность сделать модель более сбалансированной путем обеспечения постоянного во времени темпа роста выпуска продукции рыбной отрасли, зависящего от материальных затрат.
Глава 4
4.1. Построение модели Солоу
Для удобства исследования моделей экономической динамики рассматривают модели с агрегированными переменными. К ним относятся односекторные модели, в которых экономика на длительном периоде [О, Т] в каждой момент времени t ![]() [О, Т] характеризуется набором переменных X, Y, К, L, I и С, выражающих соответственно объемы валовой продукции, конечной продукции, ОПФ, рабочей силы, инвестиций и непроизводственного потребления (без учета государственных расходов). Они связаны балансовыми соотношениями:
[О, Т] характеризуется набором переменных X, Y, К, L, I и С, выражающих соответственно объемы валовой продукции, конечной продукции, ОПФ, рабочей силы, инвестиций и непроизводственного потребления (без учета государственных расходов). Они связаны балансовыми соотношениями:
![]()
где a, 0 < a < 1, — коэффициент амортизационных затрат.
![]()
![]()
![]()
Подставляя последние соотношения в первое, получим односекторную модель экономической динамики
![]() t
t ![]() [О, Т]
[О, Т]
Если t принимает дискретные значения t = 0, 1, ..., Т, то уравнение модели записывается в виде
![]()
Аналогом дискретной модели для непрерывного времени t ![]() [О, Т]
[О, Т]
является модель
![]()
где K = dK/dt. При этом переменную t обычно не записывают.
Уравнение связывает 3 переменных: X, К и С. Дальнейшие преобразования уравнения связаны с уменьшением числа переменных.
1) Пусть μ= 0, т.е. все инвестиции I полностью идут на прирост ОПФ без расходов на амортизацию. Если считать, что
![]()
то есть капитальные вложения пропорциональны приросту выпуска валовой продукции, где q > 0 называется капиталоемкостью прироста валовой продукции, то из ![]() получим односекторную динамическую модель Леонтьева
получим односекторную динамическую модель Леонтьева
![]()
2) Пусть в модели ![]() переменная X определяется с помощью производственной функции, то есть X=F(K,L) с выполнением для F всех требований для производственных функций, a L - экзогенная (управляющая) переменная с постоянным темпом роста.
переменная X определяется с помощью производственной функции, то есть X=F(K,L) с выполнением для F всех требований для производственных функций, a L - экзогенная (управляющая) переменная с постоянным темпом роста.
Отсюда следует, что ![]() , где Lo = L{0).
, где Lo = L{0).
Для удобства изучения модели перейдем к относительным переменным:
x=X/L
— производительность труда;
k = K/L
— фондовооруженность;
с=С/L
— удельное потребление.
Все эти величины являются функциями времени t. Подставляя эти выражения, получим
![]()
Сокращая все слагаемые на L, найдем
![]()
Далее, считая X=F(K,L) линейной однородной функцией, получим
![]()
или x=f(k).
При этом f(k) удовлетворяет следующим условиям:
1) f(0)=0;
2) f”(k)>0;
3) f”(k)<0;
4) f(k)→0 при k→0;
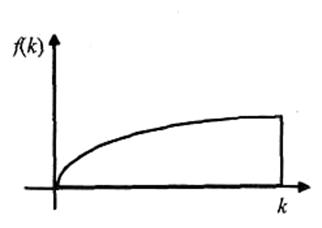
Например, этим условиям удовлетворяет степенная функция вида Кобба-Дугласа ![]() (b>0, 0<α<1).
(b>0, 0<α<1).
|
|
Неоклассическая производственная функция.
Подставляя x=f(k) в ![]() , получим открытую динамическую модель Р. Солоу
, получим открытую динамическую модель Р. Солоу
![]()
в форме дифференциального уравнения 1-го порядка со свободной (управляющей) переменной С.
Преобразуем открытую модель Солоу в замкнутую, исключив переменную С. Для этого зададим постоянную норму (долю) накопления s = I/Y и обозначим через u= С/У норму (долю) потребления, связанную с s зависимостью s + u = 1, что следует из ![]() . Отсюда следует
. Отсюда следует
![]()
Получим замкнутую динамическую модель Солоу
![]()
в форме дифференциального уравнения 1-го порядка с управляющей переменной s. Так как правая часть уравнения непрерывна, то решение k(t) уравнения существует.
Если из уравнения найти k(t), то задав L(t), найдем
![]() ,
, ![]() ,
, ![]() ,
, ![]()
и ![]() ,
,
то есть получим все переменные, характеризующие экономический процесс.
Приступим к построению динамической модели Солоу. Для начала определим экзогенные переменные.
Это Lo=14600.
Тогда, при условия постоянного темпа роста, можно составить таблицу:
| Год | L |
| 1 | 314 |
| 2 | 362 |
| 3 | 418 |
| 4 | 482 |
| 5 | 556 |
| 6 | 642 |
| 7 | 740 |
Следующая переменная, которую можно вычислить по формуле: k=K/L – это фондовооруженность.
| Год | k |
| 1 | 55 |
| 2 | 55,32 |
| 3 | 136,04 |
| 4 | 163,69 |
| 5 | 155,17 |
| 6 | 111,62 |
| 7 | 120,65 |
Следующая переменная, которую можно вычислить по формуле: x=X/L
– это производительность труда;
| Год | x |
| 1 | 324,62 |
| 2 | 528,48 |
| 3 | 398,18 |
| 4 | 249,72 |
| 5 | 166,90 |
| 6 | 130,31 |
| 7 | 137,76 |
Следующая переменная, которую можно вычислить по формуле: с=С/L
– удельное потребление.
| Год | c |
| 1 | 180,52 |
| 2 | 99,38 |
| 3 | 162,88 |
| 4 | 97,52 |
| 5 | 80,71 |
| 6 | 12,69 |
| 7 | 12,91 |
Параметр a — коэффициент амортизационных затрат, 0 < a < 1, примем равным 0,1.
Найдем параметры функции x=f(k):
| k | x |
| 55,00 | 324,62 |
| 55,32 | 528,48 |
| 136,04 | 398,18 |
| 163,69 | 249,72 |
| 155,17 | 166,90 |
| 111,62 | 130,31 |
| 120,65 | 137,76 |
x=f(k)= 4740,2*k^(-0,637).
Постоянная норма (доля) накопления s = I/Y. s=0,07.
Из уравнения ![]() найдем параметр μ. μ=0,09.
найдем параметр μ. μ=0,09.
Итак, для построения замкнутой динамической модели развития экономики Солоу ![]() известны все параметры. Формула модели выглядит следующим образом:
известны все параметры. Формула модели выглядит следующим образом:
![]()
С помощью этой формулы дифференциального уравнения 1-го порядка с управляющей переменной s можно задавать различные периоды времени и смотреть, как поведет себя при этом рыбная отрасль.
Заключение
Таким образом, мы выполнили поставленную цель курсовой работы, то есть изучили рыбную отрасль Российской Федерации с применением соответствующих разноаспектных методов.
Для реализации данной цели выполнили следующие задачи: провели анализ соответствующей литературы, выявили, какие изученные ранее экономические и математические модели могут быть пригодны для комплексного рассмотрения рыбной отрасли. Рассмотрели сильные и слабые стороны применения факторного анализа в эконометрике, а также возможности комплексных коллективных исследований, таких как метод “комиссий”, метод “Дельфи” или метод “коллективной генерации идей”.
Выявили характеристики отрасли, её особенности, которые помогли нам определиться с выбором модели для анализа. Описали технологический процесс развития рынка рыбной продукции лекарственных препаратов с 1999 по 2005 год, выявили факторы, влияющие на этот процесс, и построили многофакторную эконометрическую модель рынка лекарственных препаратов, которая выглядит следующим образом: ŷ = 287,265 +2,86*х1 -0,145*х5. Из полученного уравнения видно, что на производство рыбной продукции, тыс. тонн (фактор у) в большей степени влияют такие факторы как численность населения, на тыс. человек (фактор х1) и денежные доходы, млн. руб. (фактор х5). Причем при увеличении численности населения на тыс. человек на единицу производство рыбной продукции увеличится на 2,86 тонн, а при увеличении денежных доходов на 1 млрд руб. – уменьшится на 0,009 тонн. Получили производственные функции для рыбной продукции РФ. Выяснили, что наиболее точно производственный процесс выпуска рыбной продукции описывает линейная производственная функция, имеющая вид: F(K,L)=-9652+1,223K+28,676L.
Построили статистическую и динамическую модели Леонтьева для рыбной отрасли РФ. Для динамической модели Леонтьева учли фактор инфляции за соответствующий период. Построили магистральную модель для рыбной отрасли РФ. Провели доработку модели Леонтьева и магистральной модели, используя выявленные ранее особенности рыбной отрасли РФ. В качестве предложений по усовершенствованию функционирования экономики в рамках модели Леонтьева можно представить следующее: увеличить коэффициент прямых затрат отрасли приборо- и машиностроения с 0,2 до 0,5, а, логистики, хотя бы до 0,1, что позволит автоматизировать производство рыбной продукции, проверку их качества, а также усовершенствовать каналы сбыта и скорость движения продукции. А предложением для магистральной модели – сделать модель более сбалансированной путем обеспечения постоянного во времени темпа роста выпуска рыбной продукции, зависящего от материальных затрат. Также мы получили модель Солоу для рыбной отрасли РФ, выявив в ней экзогенные переменные.
Российская рыбная промышленность остро нуждается в привлечении иностранных инвестиций в комплексе с технологией и навыками современного управления. Рыбное производство России имеет перспективы привлечения иностранных инвесторов, однако необходимо активизировать этот процесс. Внедрение в отечественную рыбную промышленность гармонизированных с мировым сообществом правил GMP явится важным фактором содействия привлечению иностранных инвестиций. В России сделано уже многое для согласования требований к Рыбному производству с международными. Вместе с тем эту работу необходимо продолжить. Целесообразно шире использовать возможности международных организаций в этой сфере. Реализация изложенных предложений не требует ни капитальных затрат, ни объемных текущих расходов.
Список литературы:
1. Абланская Л.В. Экономико-математическое моделирование: учебник/под общ. ред. И.Н. Дрогобыцкого. – 2-е изд., стереотип. – М.: Издательство «Экзамен», 2006. – 798 [2] с. (Серия «Учебник для вузов»).
2. Айвазян С.А., Мхитарян В.С. Прикладная статистика и основы эконометрики: Учебник.- М.:ЮНИТИ,1998.
3. Елисеева И. И. Социальная статистика – Москва, Финансы и статистика, 1997 год
4. Елисеева И.И., Курышева С.В., Костеева Т.В. Эконометрика. Учебник, М.: Финансы и статистика, 2001 г.
5. Кундышева Е.С. Математическое моделирование в экономике: Учебное пособие / Под науч. Ред. проф. Б.А. Суслакова. – М.: Издательско-торговая корпорация «Дашков и К», 2004. – 352 с.
6. Кундышева Е.С. Математическое моделирование в экономике: Учебное пособие/ Под науч. ред. проф. Б.А. Суслакова. – М.: Издательско-торговая корпорация «Дашков и Ко», 2004. – 352 с.
7. Кэмпбелл Р. Макконнелл, Стенли Л. Брю Экономикс, принципы, проблемы и политика, М.: Республика, 1995
8. Мажутин В.И., Королева О.Н. Математическое моделирование в экономике: Часть III. Экономические приложения: Учебное пособие/В.И. Мажутин: – М.: Флинта: МГУ, 2004. – 176с.: ил.
9. Практикум по эконометрике: Учеб. Пособие/ И.И. Елисеева, С.В.Курышева, Н.М.Гордеенко и др.; Под ред. И.И.Елисеевой. М.: Финансы и статистика, 2002.
10. Эконометрика: Учебник/И.И. Елисеева, С.В. Курышева, Т.В. Костеева и др.; Под ред. И.И. Елисеевой. – 2-е изд., перераб. И доп. – М.: Финансы и статистика, 2005. – 576 с.: ил.
Похожие работы
... № 270 “О плане счетов бухгалтерского учета”, в котором был представлен порядок отражения лизинга в бухгалтерском учете. Развитие сети коммерческих банков способствовало внедрению лизинговых операций в банковскую практику. Российские лизинговые компании начали образовываться с середины 2000 года. В октябре 2004 года была создана Российская ассоциация лизинговых компаний “Рослизинг”. В 2004 году “ ...
... выявляют, и, по соглашению с заказчиком, копируют или излагают информацию (в случае необходимости с соответствующей верификацией) об интересующих заказчика лицах. В частности, в фондах Российского Государственного Исторического архива можно обнаружить следующие документы персонального характера: 1. Послужные списки лиц состоявших на государственной службе (за исключением самых нижних чинов, ...
... ассортимент кулинарных изделий из рыбы, их повсеместное производство у нас в стране остаётся проблематичным, это связано с нехваткой или отсутствием современных производственных мощностей. 1.4. Факторы, влияющие на формирование ассортимента рыбной кулинарии Различают общие и специфичные факторы формирования ассортимента. Общими факторами, влияющими на формирование промышленного и ...
... цены на консервную продукцию снизились за год? Это связано с тем, что руководство намерено снизило их для того, чтобы реализовать продукцию. 3 Управление себестоимостью продукции на примере ОАО «Владивостокский рыбокомбинат» 3.1 Управление себестоимостью на основе утвержденного плана выпуска продукции ОАО «Владивостокский рыбокомбинат» создал и запустил консервный цех в ...
0 комментариев