Навигация
Построение магистральной модели
2.6. Построение магистральной модели
Модели межотраслевого баланса Леонтьева позволяют планировать траекторию![]() функционирования производственного сектора экономики. Так, в рамках динамической модели Леонтьева
функционирования производственного сектора экономики. Так, в рамках динамической модели Леонтьева ![]() синхронно с траекторией валовых выпусков
синхронно с траекторией валовых выпусков ![]() строятся сопутствующие траектории основных производственных фондов
строятся сопутствующие траектории основных производственных фондов ![]() и конечных спросов
и конечных спросов ![]() .
.
С научной и практической точки зрения важно существование в рамках модели сбалансированной траектории, такой, что
![]() при t = 0, 1, 2, ...
при t = 0, 1, 2, ...
λ - const, λ > 1.
При этом траектории ![]() и
и ![]() , сопутствующие сбалансированной траектории, тоже являются сбалансированными и обладают тем же темпом роста λ, то есть
, сопутствующие сбалансированной траектории, тоже являются сбалансированными и обладают тем же темпом роста λ, то есть

Возникают два вопроса:
1) Существует ли в СММБ и ДММБ сбалансированная траектория ![]() , темп роста λ, которой максимален?
, темп роста λ, которой максимален?
2) Если ответ на первый вопрос положителен, то чем траектория ![]() лучше любой другой «хорошей» (в некотором смысле) траектории?
лучше любой другой «хорошей» (в некотором смысле) траектории?
Ответ на первый вопрос применительно к ДММБ несложно дать тотчас: константа λ в сбалансированной траектории единственна (это следует из методики ее определения, а поэтому траектория является сбалансированной траекторией с максимальным темпом роста λ. Уравнение элементов этой траектории выглядит так:
![]()
Сложнее обстоит дело с ответом на второй вопрос, поскольку этот ответ базируется на специальной теории, развитой в рамках математической экономики для исследования производственного сектора при помощи общих теоретико-аналитических моделей «затраты-выпуск». Знакомство с важнейшими понятиями и моделями этой теории составляет содержание данного пункта. В итоге будет получен ответ на второй вопрос в форме точного математического утверждения. Качественно же суть этого утверждения такова: при определенных условиях любая «хорошая» (в некотором смысле) траектория
![]() экономики лишь только на начальном и конечном временном интервале, возможно, отклоняется от магистрали
экономики лишь только на начальном и конечном временном интервале, возможно, отклоняется от магистрали ![]() . Именно данное свойство магистралей обусловливает интерес к тем моделям «затраты-выпуск», в которых магистрали существуют. Модели «затраты-выпуск», в которых существуют магистрали, принято называть магистральными.
. Именно данное свойство магистралей обусловливает интерес к тем моделям «затраты-выпуск», в которых магистрали существуют. Модели «затраты-выпуск», в которых существуют магистрали, принято называть магистральными.
Первую магистральную модель построил в 30-х годах 20-го века выдающийся американский математик Дж. фон Нейман. Эта модель, которую называют моделью расширяющейся экономики фон Неймана, отказала глубокое воздействие на математическую экономику. Подчеркнем, что СММБ Леонтьева суть частный случай модели фон Неймана.
При обсуждении модели потребуется формализация понятий производства и производственного процесса.
Под производством понимается преобразование конкретных количеств ![]() затрачиваемых продуктов в некоторые конкретные количества
затрачиваемых продуктов в некоторые конкретные количества ![]() выпускаемых продуктов. Такое преобразование осуществляется при помощи заданной технологии Т. Технологическим (или производственным) процессом называется пара (
выпускаемых продуктов. Такое преобразование осуществляется при помощи заданной технологии Т. Технологическим (или производственным) процессом называется пара (![]() ,
, ![]() ), состоящая из конкретного вектора
), состоящая из конкретного вектора ![]() затрат и конкретного вектора
затрат и конкретного вектора ![]() выпусков.
выпусков.
Рассмотрим некоторый технологический процесс (ТП) (![]() ,
, ![]() ). Чтобы подчеркнуть, что его компоненты
). Чтобы подчеркнуть, что его компоненты ![]() и
и ![]() связаны технологией Т, будем, при необходимости, обозначать ТП еще и так: (
связаны технологией Т, будем, при необходимости, обозначать ТП еще и так: (![]() Т
Т![]() ).
).
Пусть Т - какая-то заданная технология. В общем случае она позволяет реализовать некоторое множество М конкретных и различных ТП, как-то: (![]() ,
, ![]() ), (
), (![]() ,
, ![]() ), ... Все эти ТП, собранные в множество М, принято именовать технологическим множеством (ТМ) производственного сектора экономики. Так что
), ... Все эти ТП, собранные в множество М, принято именовать технологическим множеством (ТМ) производственного сектора экономики. Так что
![]()
Модель Гейла
Моделью Гейла называется ТМ, элементы ![]() которого удовлетворяют 4-м условиям, как то:
которого удовлетворяют 4-м условиям, как то:
1. Если ![]() , то
, то ![]() =0 . Это естественное свойство принято называть неосуществимостью «рога изобилия».
=0 . Это естественное свойство принято называть неосуществимостью «рога изобилия».
2. М представляет собой выпуклый конус в ![]() .
.
3. Для каждого номера i=1,2, ..., n, где n — количество компонент векторов ![]() и
и ![]() , существует ТП
, существует ТП ![]() такой, что компонента
такой, что компонента ![]() вектора
вектора ![]() положительна. Другими словами, свойство 3 означает, что каждый из n продуктов может быть произведен, так что невоспроизводимые ресурсы продуктами в модели Гейла не являются.
положительна. Другими словами, свойство 3 означает, что каждый из n продуктов может быть произведен, так что невоспроизводимые ресурсы продуктами в модели Гейла не являются.
4. Множество М замкнуто в ![]() . Это свойство, означающее, что множество М содержит все свои предельные точки, имеет сугубо математическую подоплеку, доставляющую удобство в аналитических исследованиях.
. Это свойство, означающее, что множество М содержит все свои предельные точки, имеет сугубо математическую подоплеку, доставляющую удобство в аналитических исследованиях.
Пусть М — модель Гейла. В рамках модели М естественно задается динамика развития экономики. Пусть ![]() ; будем полагать, что вектор
; будем полагать, что вектор ![]() потребляется (в процессе производства) в текущий момент времени t, а вектор
потребляется (в процессе производства) в текущий момент времени t, а вектор ![]() производится в следующий момент (t+1). Тогда
производится в следующий момент (t+1). Тогда ![]() характеризует состояние экономики (в смысле запаса продуктов) в текущий момент t. Аналогично, вектор
характеризует состояние экономики (в смысле запаса продуктов) в текущий момент t. Аналогично, вектор ![]() характеризует состояние экономики в следующий момент (t + 1), причем пара
характеризует состояние экономики в следующий момент (t + 1), причем пара ![]() . Далее, вектор
. Далее, вектор ![]() будет потребляться в момент (t + 1), а в момент (t + 2) окажется произведенным вектор
будет потребляться в момент (t + 1), а в момент (t + 2) окажется произведенным вектор ![]() и т.д. Таким образом, осуществляется динамическое движение экономики
и т.д. Таким образом, осуществляется динамическое движение экономики
![]()
Это движение самоподдерживающееся, поскольку какой-либо приток извне, полагаем, отсутствует.
Последовательность ![]() называется допустимой траекторией в модели Гейла М на конечном интервале времени Т, если при t = 0, 1, 2, ..., T-1 справедливо отношение
называется допустимой траекторией в модели Гейла М на конечном интервале времени Т, если при t = 0, 1, 2, ..., T-1 справедливо отношение ![]() . Если Т бесконечно, то траектория
. Если Т бесконечно, то траектория
![]() допустима на бесконечном интервале времени. Не равная тождественно нулю допустимая траектория
допустима на бесконечном интервале времени. Не равная тождественно нулю допустимая траектория ![]() называется траекторией сбалансированного роста, если при t = 0, 1, 2,... справедливо равенство
называется траекторией сбалансированного роста, если при t = 0, 1, 2,... справедливо равенство
![]() ,
,
в котором λ - положительная константа, темп роста сбалансированной траектории. Сбалансированная траектория ![]() называется магистралью, если ее темп роста λ максимален.
называется магистралью, если ее темп роста λ максимален.
Как следует из данного определения, магистраль, если она существует, принадлежит при всех t = 0, 1,2,... лучу
![]() .
.
Этот луч принято называть неймановским лучом.
Понятие темпа роста определено выражением ![]() применительно к сбалансированным траекториям модели Гейла.
применительно к сбалансированным траекториям модели Гейла.
Рассмотрим сначала специальное подмножество Мо![]() М тривиальных ТП модели Гейла, то есть таких процессов
М тривиальных ТП модели Гейла, то есть таких процессов ![]() , у которых
, у которых ![]() . Можно показать (см. задачу 18 в конце гл. 9), пользуясь определением модели Гейла, что подмножество Мо состоит из одного элемента (
. Можно показать (см. задачу 18 в конце гл. 9), пользуясь определением модели Гейла, что подмножество Мо состоит из одного элемента (![]() ,
,![]() ). Его темп роста определяем следующим образом
). Его темп роста определяем следующим образом
λ(![]() ,
,![]() ) = 0.
) = 0.
Пусть теперь ![]() - любой нетривиальный ТП; его темп роста
- любой нетривиальный ТП; его темп роста ![]() определяется так:
определяется так:
![]()
В правой части последнего равенства минимум берется по всем положительным компонентам вектора ![]() .
.
Рассмотрим 2 последних выражения (9.6.16)-(9.6.17), задающих определение темпа роста ![]() любого ТП
любого ТП ![]() , или говоря иначе, определяющие на множестве М скалярную неотрицательную функцию
, или говоря иначе, определяющие на множестве М скалярную неотрицательную функцию ![]() . Каковы свойства этой функции? Отметим три из них.
. Каковы свойства этой функции? Отметим три из них.
1. Функция ![]() является положительно однородной функцией нулевой степени, то есть
является положительно однородной функцией нулевой степени, то есть
![]() ,
,
при любом (![]() > 0).
> 0).
2. Значение функции ![]() удовлетворяет неравенству
удовлетворяет неравенству
![]()
3. В множестве М существует такой ТП ![]() , что
, что
![]()
причем справедливо неравенство
![]() .
.
Итак, для фармацевтической отрасли представлены данные по валовому выпуску и осуществленным соответствующим затратам для семи лет. Сведем эти данные в таблицу:
| Материальные затраты, x | Выпуск, y | |
| 1 | 87573 | 101964 |
| 2 | 95515,9 | 191487 |
| 3 | 109837,86 | 166431 |
| 4 | 71931 | 120408 |
| 5 | 75687,8 | 92829 |
| 6 | 72835,49 | 83607 |
| 7 | 80921,5 | 101964 |
Графически это будет представлено так:
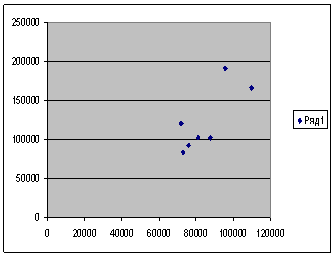
Неймановский луч, определяемый по формуле ![]() ,
,
выглядит на графике следующим образом.
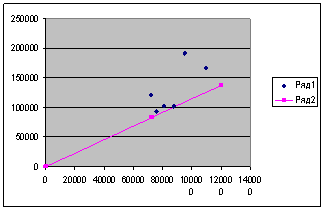
Тогда из представленного соотношения найдем темп роста экономики:
![]()
Константа λ в сбалансированной траектории единственна (это следует из методики ее определения, а поэтому траектория является сбалансированной траекторией с максимальным темпом роста λ. Уравнение элементов этой траектории выглядит так:
![]()
Тогда сбалансированная траектория выглядит следующим образом:
| Материальные затраты, x | Сбал. выпуск, y | |
| 1 | 87573 | 100524,0139 |
| 2 | 95515,9 | 109641,5752 |
| 3 | 109837,86 | 126081,5841 |
| 4 | 71931 | 82568,7466 |
| 5 | 75687,8 | 86881,13301 |
| 6 | 72835,49 | 83607 |
| 7 | 80921,5 | 92888,83552 |
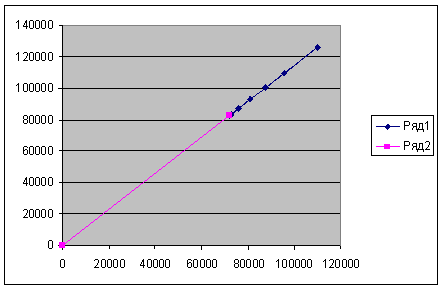
Глава 3
Похожие работы
... № 270 “О плане счетов бухгалтерского учета”, в котором был представлен порядок отражения лизинга в бухгалтерском учете. Развитие сети коммерческих банков способствовало внедрению лизинговых операций в банковскую практику. Российские лизинговые компании начали образовываться с середины 2000 года. В октябре 2004 года была создана Российская ассоциация лизинговых компаний “Рослизинг”. В 2004 году “ ...
... выявляют, и, по соглашению с заказчиком, копируют или излагают информацию (в случае необходимости с соответствующей верификацией) об интересующих заказчика лицах. В частности, в фондах Российского Государственного Исторического архива можно обнаружить следующие документы персонального характера: 1. Послужные списки лиц состоявших на государственной службе (за исключением самых нижних чинов, ...
... ассортимент кулинарных изделий из рыбы, их повсеместное производство у нас в стране остаётся проблематичным, это связано с нехваткой или отсутствием современных производственных мощностей. 1.4. Факторы, влияющие на формирование ассортимента рыбной кулинарии Различают общие и специфичные факторы формирования ассортимента. Общими факторами, влияющими на формирование промышленного и ...
... цены на консервную продукцию снизились за год? Это связано с тем, что руководство намерено снизило их для того, чтобы реализовать продукцию. 3 Управление себестоимостью продукции на примере ОАО «Владивостокский рыбокомбинат» 3.1 Управление себестоимостью на основе утвержденного плана выпуска продукции ОАО «Владивостокский рыбокомбинат» создал и запустил консервный цех в ...
0 комментариев