Навигация
Модель олигополии Бертрана
3.2 Модель олигополии Бертрана
Обобщение модели Бертрана для случая п фирм в отрасли фактически не изменяет основные характеристики равновесия на рынке. Логика процесса принятия решений при предпосылках (1)-(3) остается прежней.
Таким образом, ценовая война будет продолжаться до тех пор, пока цена не снизится до уровня предельных и средних издержек. Олигополисты независимо друг от друга вынуждены будут установить одну и ту же цену (![]() ) обеспечивая рыночный спрос на уровне предложения на рынке совершенной конкуренции. Олигополисты Бертрана по-прежнему не смогут получить положительную прибыль и, следуя предпосылкам модели, в условиях равновесия разделяет рынок между собой. Доля предложения каждой фирмы на рынке составит п-ю часть рыночного спроса:
) обеспечивая рыночный спрос на уровне предложения на рынке совершенной конкуренции. Олигополисты Бертрана по-прежнему не смогут получить положительную прибыль и, следуя предпосылкам модели, в условиях равновесия разделяет рынок между собой. Доля предложения каждой фирмы на рынке составит п-ю часть рыночного спроса:
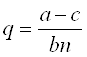
(3.8)
Очевидно, что при одинаковом количестве фирм на рынке олигополист Бертрана в условиях равновесия предлагает на рынок больше продукции, чем олигополист Курно (достаточно сравнить (3.4) и (3.8)), а рыночный спрос удовлетворяется в большем объеме при более низкой цене.
С увеличением числа фирм на рынке изменяется только один параметр рыночного равновесия: уменьшается доля предложения каждой отдельной фирмы. В результате при значительном увеличении числа фирм на рынке (при ![]() ) уровень выпуска отдельной фирмы становится слишком мал по сравнению с размерами рынка. В этом крайнем случае рынок олигополии Бертрана, как и рынок Курно, трансформируется в рынок совершенной конкуренции.
) уровень выпуска отдельной фирмы становится слишком мал по сравнению с размерами рынка. В этом крайнем случае рынок олигополии Бертрана, как и рынок Курно, трансформируется в рынок совершенной конкуренции.
Пусть две фирмы на рынке предлагают однородную продукцию, зная функцию рыночного спроса (1), но имеют неравные условия по издержкам производства:
(3.9)
где с1, с2 - положительные константы.
Пусть для определенности c1 меньше с2. Таким образом, у обеих фирм предельные издержки по-прежнему равны средним, но у первой фирмы из уровень меньше (c1 <с2).
При данных предпосылках ценовая война неизбежна. Предположим, что ценовая война привела к понижению цены до уровня средних издержек второй фирмы (c2). Равновесие на рынке при такой цене не может быть достигнуто, поскольку первая фирма ещё способна получить выгоду от снижения цены.
Допустим, что первая фирма назначит цену на уровне
![]()
(3.10)
где ![]() .
.
Верхняя граница изменения ![]() существует, поскольку фирме невыгодно устанавливать цену ниже уровня средних и предельных издержек. Если цена, назначенная первой фирмой, выше её средних издержек (с1), но ниже средних издержек фирмы-конкурента (с2), то первая фирма сможет привлечь покупателей боле низкой ценой и получить положительную прибыль.
существует, поскольку фирме невыгодно устанавливать цену ниже уровня средних и предельных издержек. Если цена, назначенная первой фирмой, выше её средних издержек (с1), но ниже средних издержек фирмы-конкурента (с2), то первая фирма сможет привлечь покупателей боле низкой ценой и получить положительную прибыль.
Производственная деятельность второй фирмы окажется убыточной. Продолжение ценовой войны будет увеличивать убытки второй фирмы.
Обобщая модель для случая n фирм в отрасли, можно сделать следующие выводы. При заданных условиях стратегического взаимодействия в выигрышной ситуации окажутся те фирмы, чей уровень средних и предельных издержек будет ниже. Следовательно, число фирм на рынке может сократиться.
Равновесие на рынке олигополии Бертрана также не будет единственным и, в частности, может быть достигнуто, если одна или несколько фирм смогут наладить безубыточное производство при одном и том же уровне рыночной цены.
3.3 Модель олигополии Стэкльберга
При предпосылках (1) - (3) стратегическое взаимодействие по принципу «лидер-последователь» не выгодно для обеих фирм: характеристики равновесия во многом неудовлетворительны даже для лидера, и вряд ли кто-то из конкурентов захочет быть последователем. Обобщение модели дуополии Стэкльберга при таких предпосылках не поможет ответить на вопрос, почему из множества идентичных фирм только одна окажется лидером по объему выпуска.
Пусть фирмы, как и ранее, производят однородную продукцию, зная линейную функцию рыночного спроса (1). Пусть только одна фирма (условно -первая фирма) имеет преимущество в издержках над всеми конкурентами. Сохраним предпосылку, что у всех фирм на рынке предельные издержки постоянны и равны средним издержкам.
При таких предпосылках введем обозначения. Пусть cL - предельные и средние издержки первой фирмы (лидера); cf - предельные и средние издержки каждой фирмы-последователя, где cL<cf . Пусть на рынке олигополии взаимодействуют одна фирма-лидер и п фирм-последователей, т.е. рыночный спрос обеспечивают (п + 1) фирм:
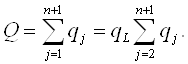
(3.11)
Последователи вынуждены признать преимущество фирмы-лидера, ибо при значительном возрастании объема предложения рыночная цена может опуститься ниже уровня средних издержек фирмы-последователя, оставаясь при этом выше уровня средних издержек фирмы-лидера (cL<p<cf). Значит, увеличив масштабы производства, фирма-лидер при определенных условиях может получать положительную прибыль, в то время как ее конкуренты будут иметь убытки.
Таким образом, каждый последователь осознает лидерство первой фирмы, рассматривает уровень ее выпуска как заданный и решает задачу на максимум прибыли при нулевых предполагаемых вариациях. Учитывая условие (3.11), функцию прибыли олигополиста (3.2) можно записать для фирмы-последователя в виде:
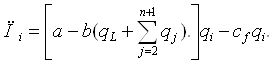
(3.12)
Необходимое условие экстремума (3.3) примет вид:
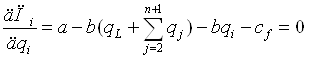
(3.13)
Обратим внимание на то, что в модели олигополии Стэкльберга последователь рассматривает уровень выпуска любого конкурента как постоянный, последователи ведут себя как олигополисты Курно.
Используем для фирм-последователей тот же алгоритм решения модели, который упростил решение задачи при анализе модели олигополии Курно. Все фирмы-последователи находятся в одинаковых условиях. Следовательно, при достижении равновесия будут предлагать на рынок равные объемы производства qf. Условие (3.13) запишем в более удобном виде:
![]() (3.14)
(3.14)
откуда легко получить функцию реакции любой фирмы-последователя:
![]() (3.15)
(3.15)
Фирма-лидер информирована о поведении последователей. Она осознает, что каждый последователь реагирует на изменение объема выпуска фирмы-лидера в соответствии со своей функцией реакции (3.15). Функция реакции определяет значение предполагаемой вариации:
![]()
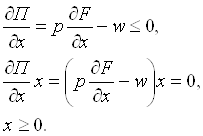
Учитывая возможную реакцию последователей, первая фирма решает задачу на максимум прибыли:
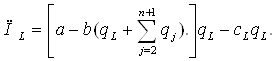
(3.17)
Необходимое условие экстремума примет вид:
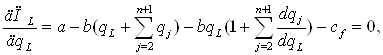
(3.18)
где в точке равновесия 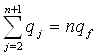 ,
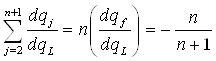
, 
делав необходимые преобразования, получим функцию реакции фирмы-лидера:

(3.18)
которая показывает, каким должен быть наилучший ответ на действия последователя.
Если на рынке олигополии Стэкльберга более одного последователя, то ![]() Предположим, что фирма-последователь уменьшит объем выпуска на единицу. Предполагаемая вариация
Предположим, что фирма-последователь уменьшит объем выпуска на единицу. Предполагаемая вариация ![]() указывает, что тогда фирма-лидер может поставлять на рынок объем товара, больший единицы. Тем самым увеличится доля рыночного спроса, удовлетворяемая с меньшими издержками производства.
указывает, что тогда фирма-лидер может поставлять на рынок объем товара, больший единицы. Тем самым увеличится доля рыночного спроса, удовлетворяемая с меньшими издержками производства.
Решая систему уравнений (3.15), (3.19), можно рассчитать равновесные уровни выпуска фирмы-л ид ера и фирмы-последователя:
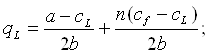
(3.20)
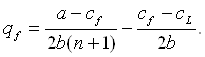
(3.21)
В условиях равновесия олигополисты Стэкльберга удовлетворяют рыночный спрос в объеме
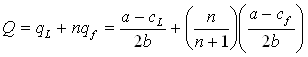
(3.22)
при рыночной цене
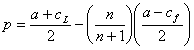
(3.23)
Посмотрим, что произойдет на рынке олигополии Стэкльберга при изменении двух параметров: числа фирм-последователей (п) и размера преимущества фирмы-лидера в издержках (cf-cL). Очевидно, сто рост обоих
параметров оказывает одинаковое влияние на объем предложения фирм на рынке см. (3.20), (3.21). Объем предложения лидера увеличивается, а объем предложения каждого последователя уменьшается.
Как следствие, должно произойти увеличение доли лидера на рынке. Однако, как показывает исследование, прослеживается достаточно сложная функциональная зависимость доли лидера от числа фирм-последователей и размера преимущества лидера в издержках. Только в конечном итоге большое число конкурентов увеличивает значение преимущества лидера, и его доля на рынке начинает расти.
Интересно, что с ростом числа последователей, когда коэффициент ![]() стремится к единице, равновесная цена постепенно снижается и приближается к среднему арифметическому средних издержек лидера и последователя
стремится к единице, равновесная цена постепенно снижается и приближается к среднему арифметическому средних издержек лидера и последователя 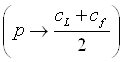 . Такой уровень цены превышает средние издержки лидера, но ниже средних издержек последователя. Конкурентоспособность последователей падает, их число должно уменьшиться. Преимущество лидера в издержках подтверждает обоснованность его притязаний на лидерство.
. Такой уровень цены превышает средние издержки лидера, но ниже средних издержек последователя. Конкурентоспособность последователей падает, их число должно уменьшиться. Преимущество лидера в издержках подтверждает обоснованность его притязаний на лидерство.
Теперь рассмотрим частный случай модели, когда все фирмы имеют равные
условия по издержкам производства (cL=cf=c). Основные параметры рыночного равновесия можно получить из формул (3.20) - (3.23):
![]()
(3.24)
![]()
(3.25)
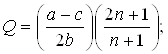
(3.26)

(3.27)
Очевидно, что объем предложения фирмы-лидера не зависит от числа последователей. Объем предложения фирмы-последователя в (n + 1) раз меньше, чем у лидера, и постепенно сокращается с увеличением числа последователей.
При достаточно большом числе последователей (когда ![]() ) объем предложения олигополистов Стэкльберга приближается к объему предложения в условиях совершенной конкуренции
) объем предложения олигополистов Стэкльберга приближается к объему предложения в условиях совершенной конкуренции ![]() , а цена фактически падает до уровня средних и предельных издержек.
, а цена фактически падает до уровня средних и предельных издержек.
При этом все существеннее становится различие в уровне выпуска лидера и последователя. Доля последователя в совокупном объеме предложения на рынке ![]() становится бесконечно мала по сравнению с размерами рынка. Доля лидера
становится бесконечно мала по сравнению с размерами рынка. Доля лидера ![]() тоже постепенно снижается, но в конечном итоге не будет ниже, чем половина объема предложения на рынке.
тоже постепенно снижается, но в конечном итоге не будет ниже, чем половина объема предложения на рынке.
Похожие работы
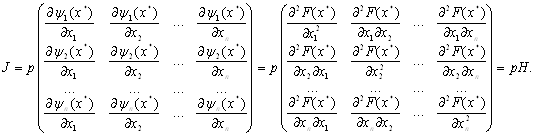
... |Н| производственной функции (но Н отрицательно определена, поэтому действительно |Н| =0). Тогда х* = х* (р,w) (12) или хj* = хj* (р,w), j = 1,…,n Эти п уравнений задают функции спроса (на ресурсы), найденные с помощью модели поведения фирмы. Функции спроса на ресурсы могут быть также найдены экспериментально с помощью методов математической статистики по выборочным данным
... , количество фирм в отрасли. Все это в совокупности порождает множественность существующих моделей олигополии. Ни одну из этих моделей нельзя считать универсальной, хотя общую логику поведения производителя на рынке они все же отражают. 3.2.1 Модель дуополии Антуана Огустина Курно Первая модель олигополии была разработана французским экономистом и математиком Антуаном Огустином Курно в 1838 г. ...
... ; товары являются комплектными, если В этом случае рост производства одного товара необходимо вызывает увеличение выпуска другого. 3. Практическое применение производственной функции 3.1 Моделирование издержек и прибыли предприятия (фирмы) В основе построения моделей поведения производителя (отдельного предприятия или фирмы; объединения или отрасли) лежит представление о том, что ...
... Данные авторского исследования также говорят о значительном влиянии СМИ с точки зрения самих студентов (табл. 2.6). Гипотеза 3. Усиление влияния процессов в сфере моды на социальное поведение студенчества связано с возрастающим влиянием СМИ и рекламы на поведение современной молодежи в условиях «общества потребления». Для того чтобы опровергнуть или подтвердить это гипотетическое заключение, ...
0 комментариев