Навигация
Перепишем уравнение Ван-дер-Ваальса в виде полинома по объему
16804
знака
2
таблицы
0
изображений
2. Перепишем уравнение Ван-дер-Ваальса в виде полинома по объему
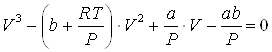.(6.4)
Корни данного уравнения можно найти, воспользовавшись формулами Кардано. Для этого перейдем к приведенному виду кубического уравнения, выполнив следующие преобразования. Обозначим коэффициенты в уравнении (6.4) через
; 
; 
и сделаем замену неизвестного V на Y:
;
тогда уравнение (6.4) примет приведенный вид
,(6.5)
где 
; 
.
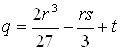Число действительных решений кубического уравнения зависит от знака дискриминанта
.(6.6)
Если D > 0, то уравнение имеет одно действительное решение; если D < 0, то - три действительных решения; и если D = 0, то уравнение имеет либо два действительных решения, одно из которых двукратное, либо одно действительное трехкратное решение (последнее в случае p = q = 0).
В данном примере рассматривается область P-V-T пространства, где сосуществуют пар и жидкость. Для этой области уравнение Ван-дер-Ваальса имеет три действительных решения (дискриминант уравнения (6.5) меньше нуля). При использовании формул Кардано в оригинальном виде корни уравнения выражаются через комплексные величины. Избежать этого можно, если ввести следующие обозначения:
, 
.(6.7)
Тогда решениями приведенного уравнения (6.5) будут
;(6.8)
;(6.9)
,(6.10)
от которых заменой
(6.11)
снова можно перейти к решениям кубического уравнения (6.4).
3. Вычислим характеристические константы уравнения Ван-дер-Ваальса. Для удобства вычислений примем следующие единицы измерения: V - л/моль , P - атм, Т - К. Тогда R = 0,08206 л·атм/(моль·К);
a = 27·0,082062·6502/(64·31)=38,72 л·атм;
b = 0,08206·650/(8·31)=0,2151 л.
4. Давление насыщения находится методом последовательных приближений. В качестве первого приближения при Т = 400 К примем давление насыщения равным 10 атм.
5. Рассчитаем значения коэффициентов уравнения (6.4):
= –(0,2151+0,08206·400/10) = – 3,4975;
= 38,72/10 = 3,872;
= – (38,72·0,2151/10) = – 0,8329.
6. Далее вычислим коэффициенты приведенного кубического уравнения (6.5) и значение дискриминанта D:
= [3·3,872–(–3,4975)2]/3 = – 0,2055;
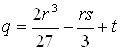= 2·(–3,4975)3/27–(–3,4975·3,872)/3+(–0,8329)=0,5121;
= (–0,2055/3)3+(0,5121/2)2 = 0,0652.
Значение дискриминанта (D) получилось положительным, что говорит о единственном действительном решении уравнения (6.5). Следовательно, значение давления выбрано неверно.
7. Предположим, что давление насыщения равно 1 атм. Повторим вычисления в пунктах 5 и 6.
= –(0,2151+0,08206·400/1) = –33,04;
= 38,72/1 = 38,72;
= –(38,72·0,2151/1) = –8,329;
=[3·38,72 –(–33,04)2]/3 = –325,2;
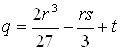= 2·(–33,04)3/27 –(–33,04·38,72)/3+(–8,329) = –2254;
= (–325,2/3)3+(–2254/2)2 = –3632.
Значение D отрицательное, следовательно, уравнение имеет три действительных решения.
8. Найдем эти решения, но прежде вычислим вспомогательные величины 
и
= [–(–325,2)3/27]1/2 = 1129;
= –(–2254)/(2·1129) = 0,9982;
= arccos (0,9982) = 0,0600 радиан;
= 2·(1129)1/3·cos(0,0600/3) = 20,82;
= 2·(1129)1/3 cos(0,0600/3 + 2·3,14/3) = –10,75;
= 2·(1129)1/3 cos (0,0600/3 + 4·3,14/3) = –10,09.
Похожие работы
... -7 -47,5 Двойная связь между атомами углерода 7 – Тройная связь между атомами углерода 14 – Неаддитивный метод Тина и Каллуса Величина мольного объема жидкости при нормальной температуре кипения представлена в качестве функции критического объема: ,(6.13) где и выражены в см3/моль. Это простое соотношение хорошо прогнозирует для органических чистых жидкостей, погрешность ...
... Выпишем парциальные вклады для температуры, давления и объема: Группа к-во ΔT ΔP СН2 (цикл) 4 0,04 -0,0112 Сумма 4 0,04 -0,0112 Критическая температура. Критическое давление. ; о-Ксилол, 1,2-диметилбензол Выпишем парциальные вклады для температуры, давления и объема: Группа кол-во ΔT ΔP CН3 2 0,0282 -0,0024 -СН=(цикл) 4 0, ...
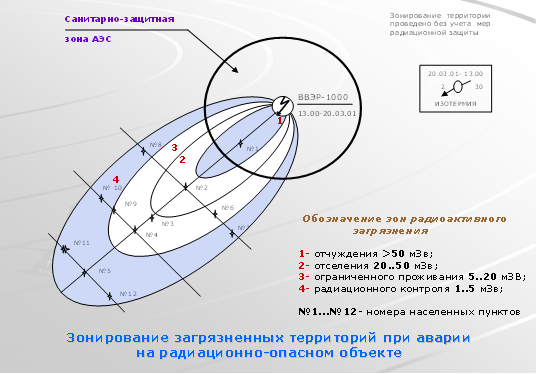
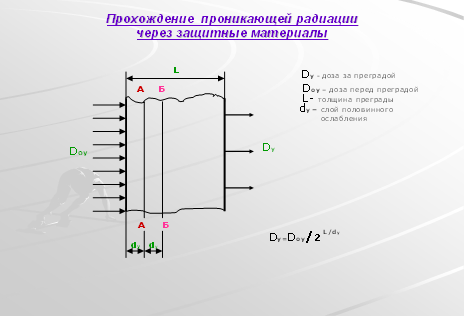
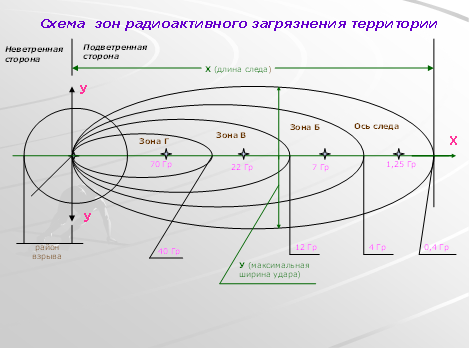
... степени, 10% —второй. Таким образом, наибольшую опасность представляют бескаркасные здания без фундамента из местных материалов, жители которых могут серьезно пострадать. Прогнозирование и оценка обстановки при чрезвычайных ситуациях природного характера осуществляется с использованием специальных методик и рекомендаций , часть некоторых из них изложена в данной методичке и в учебном пособии « ...
... Задание №5 Для первого соединения рассчитать плотность вещества при температуре 730 К и давлении 100 бар. Определить фазовое состояние компонента. Для определения плотности вещества воспользуемся методом прогнозирования плотности индивидуальных веществ с использованием коэффициента сжимаемости. где -плотность вещества; М- молярная масса; V-объем. Для данного вещества найдем коэффициент ...
0 комментариев