Навигация
Перейдем к решениям уравнения (6.4), воспользовавшись (6.11)
9. Перейдем к решениям уравнения (6.4), воспользовавшись (6.11).
![]() = 20,82 –(–33,04/3) = 31,8 л/моль;
= 20,82 –(–33,04/3) = 31,8 л/моль;
![]() = –10,75 –(–33,04/3) = 0,263 л/моль;
= –10,75 –(–33,04/3) = 0,263 л/моль;
![]() = –10,09 –(–33,04/3) = 0,923 л/моль.
= –10,09 –(–33,04/3) = 0,923 л/моль.
При 400 К и 1 атм объем пара (V1) составляет 31,8 л/моль, объем жидкости (V2) – 0,263 л/моль. V3 = 0,923 – третий корень уравнения, не имеющий физического смысла.
10. Вычислим значение левой части выражения (6.3), для этого имеются все необходимые величины:
 = 0,08206·400 ln[(31,8–0,2151)/
= 0,08206·400 ln[(31,8–0,2151)/
/(0,263– 0,2151)] + 38,72·(1/31,8–1/0,263)–1·(31,8–0,263) = 35,53.
При избранном давлении (1 атм ) выражение (6.3) в тождество не обращается, т.е. левая и правая части не равны друг другу. Необходимо принять другое значение давления насыщения.
В пунктах 5-10 вычисления производились с округлением промежуточных величин на каждом шаге вычислений до значений, записанных в формулах. Далее приводятся результаты вычислений с точностью в 16 десятичных разрядов, и округление выполнено только при представлении окончательных величин.
11. Примем Psat = 3 атм. Повторим вычисления в пунктах 5-10. При 400 К и 3 атм объем пара составляет 9,878 л/моль, объем жидкости – 0,282 л/моль. Левая часть выражения (6.3) равна ![]() = 1,0515. Тождество не выполняется, но степень отклонения от него существенно уменьшилась.
= 1,0515. Тождество не выполняется, но степень отклонения от него существенно уменьшилась.
12. Подбор давления насыщения следует продолжить. Теперь имеется два значения для левой части выражения (6.3) при соответствующих давлениях. Используя эти величины, можно оценить значение давления для следующего расчета путем линейной интерполяции.
![]() = 1–(1–3)/(35,53–1,0515)·35,53 = 3,061 атм.
= 1–(1–3)/(35,53–1,0515)·35,53 = 3,061 атм.
13. Повторим вычисления (пункты 5-12) для Psat = 3,061 атм. Получим:
![]() = 9,658 л/моль;
= 9,658 л/моль; ![]() = 0,282 л/моль;
= 0,282 л/моль; ![]() = 0,473. Новое значение давления – 3,111 атм.
= 0,473. Новое значение давления – 3,111 атм.
После 5 итераций, исключая расчет при Psat = 10 атм, имеем:
T = 400 K; P sat = 3,112 атм; ![]() = 9,480 л/моль;
= 9,480 л/моль; ![]() = 0,282 л/моль;
= 0,282 л/моль; ![]() = 8,7·10-5. Полученные значения давления и объемов жидкости и пара соответствуют условиям насыщения.
= 8,7·10-5. Полученные значения давления и объемов жидкости и пара соответствуют условиям насыщения.
14. Результаты расчета для других температур приведены в табл. 6.3.
Таблица 6.3
| Т, К | Psat, атм |
|
|
| 400 | 3,112 | 0,282 | 9,480 |
| 500 | 9,888 | 0,322 | 3,235 |
| 600 | 22,328 | 0,410 | 1,322 |
| 640 | 29,127 | 0,515 | 0,850 |
15. Область метастабильных (пересыщенных) состояний пара и жидкости занимает пространство между бинодалью и спинодалью. Точки на изотермах, принадлежащие бинодали, определены выше, и их значения приведены в табл. 6.3.
Для определения конфигурации спинодали воспользуемся соотношением
![]() ,
,
т.е. условиями экстремальности для соответствующих точек изотермы. Далее продифференцируем уравнение Ван-дер-Ваальса по объему (при Т = const) и преобразуем полученное выражение к полиному по V. Получим кубическое уравнение (6.12), корни которого могут быть найдены изложенным выше способом (п.п. 5-9):
 .(6.12)
.(6.12)
16. Для 400 К имеем следующие значения коэффициентов уравнения (6.12):
![]() = –[2·38,72/(0,08206·400)] = –2,3593;
= –[2·38,72/(0,08206·400)] = –2,3593;
![]() = [4·38,72·0,2151/(0,08206·400)] = 1,0149;
= [4·38,72·0,2151/(0,08206·400)] = 1,0149;
![]() = –[2·38,72·0,21512/(0,08206·400)] = –0,1092.
= –[2·38,72·0,21512/(0,08206·400)] = –0,1092.
Коэффициенты приведенного кубического уравнения (6.5) соответственно равны:
 = [3·1,0149 –(–2,3593)2]/3 = –0,8405;
= [3·1,0149 –(–2,3593)2]/3 = –0,8405;
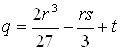 = 2·(–2,3593)3/27 –(–2,3593·1,0149)/3 + (–0,1092) = –0,2838;
= 2·(–2,3593)3/27 –(–2,3593·1,0149)/3 + (–0,1092) = –0,2838;
![]() = (–0,8405/3)3 + (–0,2838/2)2 = –0,0019.
= (–0,8405/3)3 + (–0,2838/2)2 = –0,0019.
Значение D отрицательное, следовательно, уравнение имеет три действительных решения.
17. Найдем значения корней уравнения (6.12) при 400 К. Для этого выполним последовательно следующие вычисления:
![]() = [–(–0,8405)3/27]1/2 = 0,1483;
= [–(–0,8405)3/27]1/2 = 0,1483;
![]() = –(–0,2838)/(2·0,1483) = 0,9568;
= –(–0,2838)/(2·0,1483) = 0,9568;
![]() = arccos (0,9568) = 0,2950 радиан;
= arccos (0,9568) = 0,2950 радиан;
![]() = 2·(0,1483)1/3 cos(0,2950/3) = 1,0535;
= 2·(0,1483)1/3 cos(0,2950/3) = 1,0535;
![]() = 2·(0,1483)1/3 cos(0,2950/3 + 2·3,14/3) = –0,6159;
= 2·(0,1483)1/3 cos(0,2950/3 + 2·3,14/3) = –0,6159;
![]() = 2·(0,1483)1/3 cos(0,2950/3 + 4·3,14/3) = –0,4388;
= 2·(0,1483)1/3 cos(0,2950/3 + 4·3,14/3) = –0,4388;
![]() = 1,0535 –(–2,3593/3) = 1,840 л/моль;
= 1,0535 –(–2,3593/3) = 1,840 л/моль;
![]() = –0,6159 –(–2,3593/3) = 0,171 л/моль;
= –0,6159 –(–2,3593/3) = 0,171 л/моль;
![]() = –0,4388 –(–2,3593/3) = 0,348 л/моль.
= –0,4388 –(–2,3593/3) = 0,348 л/моль.
Наибольший корень ![]() = 1,840 л/моль соответствует максимуму на изотерме 400 К и ограничивает метастабильные состояния пара слева. Корень
= 1,840 л/моль соответствует максимуму на изотерме 400 К и ограничивает метастабильные состояния пара слева. Корень ![]() , равный 0,171 л/моль, не имеет физического толкования, поскольку его значение меньше параметра b в уравнении Ван-дер-Ваальса. И, наконец, корень
, равный 0,171 л/моль, не имеет физического толкования, поскольку его значение меньше параметра b в уравнении Ван-дер-Ваальса. И, наконец, корень ![]() соответствует минимуму на изотерме 400 К и отделяет слева область пересыщенной жидкости от абсолютно неустойчивых состояний.
соответствует минимуму на изотерме 400 К и отделяет слева область пересыщенной жидкости от абсолютно неустойчивых состояний.
18. Давление в системе при соответствующем объеме пересыщенного пара (![]() ) и пересыщенной жидкости (
) и пересыщенной жидкости (![]() ) находится из уравнения Ван-дер-Ваальса подстановкой в него требуемых значений температуры и объема.
) находится из уравнения Ван-дер-Ваальса подстановкой в него требуемых значений температуры и объема.
 = (0,08206·400)/(1,840–0,215)–38,72/1,8402 = 8,763 атм;
= (0,08206·400)/(1,840–0,215)–38,72/1,8402 = 8,763 атм;
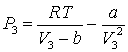 = (0,08206·400)/(0,348–0,215)–38,72/0,3482 = –72,928 атм.
= (0,08206·400)/(0,348–0,215)–38,72/0,3482 = –72,928 атм.
19. Результаты расчета для прочих температур приведены в табл. 6.4.
| Т, К |
|
|
|
|
| 400 | -72,928 | 0,348 | 8,763 | 1,840 |
| 500 | -20,124 | 0,397 | 14,913 | 1,324 |
| 600 | 17,803 | 0,482 | 24,103 | 0,929 |
| 640 | 28,798 | 0,563 | 29,347 | 0,750 |
Похожие работы
... -7 -47,5 Двойная связь между атомами углерода 7 – Тройная связь между атомами углерода 14 – Неаддитивный метод Тина и Каллуса Величина мольного объема жидкости при нормальной температуре кипения представлена в качестве функции критического объема: ,(6.13) где и выражены в см3/моль. Это простое соотношение хорошо прогнозирует для органических чистых жидкостей, погрешность ...
... Выпишем парциальные вклады для температуры, давления и объема: Группа к-во ΔT ΔP СН2 (цикл) 4 0,04 -0,0112 Сумма 4 0,04 -0,0112 Критическая температура. Критическое давление. ; о-Ксилол, 1,2-диметилбензол Выпишем парциальные вклады для температуры, давления и объема: Группа кол-во ΔT ΔP CН3 2 0,0282 -0,0024 -СН=(цикл) 4 0, ...
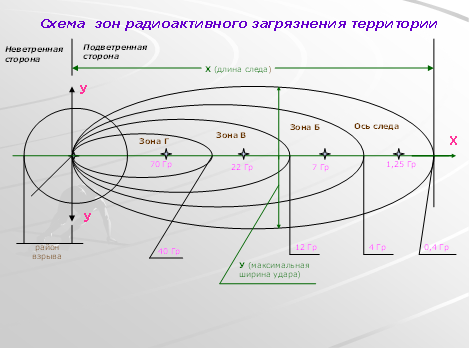
... степени, 10% —второй. Таким образом, наибольшую опасность представляют бескаркасные здания без фундамента из местных материалов, жители которых могут серьезно пострадать. Прогнозирование и оценка обстановки при чрезвычайных ситуациях природного характера осуществляется с использованием специальных методик и рекомендаций , часть некоторых из них изложена в данной методичке и в учебном пособии « ...
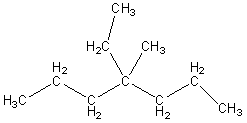
... Задание №5 Для первого соединения рассчитать плотность вещества при температуре 730 К и давлении 100 бар. Определить фазовое состояние компонента. Для определения плотности вещества воспользуемся методом прогнозирования плотности индивидуальных веществ с использованием коэффициента сжимаемости. где -плотность вещества; М- молярная масса; V-объем. Для данного вещества найдем коэффициент ...
0 комментариев