Центральная симметрия

4. Центральная симметрия.

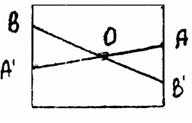
Задача. Построить квадрат, если даны его центр О и две точки А и В на параллельных его сторонах.

Анализ. Пусть искомый квадрат построен. Тогда А’ и В, где лежат на А’ = Z₀ (A), лежат на одной стороне квадрата. Аналогично В’ и А, где В' = Z₀ (в), лежат на одной стороне квадрата. Тогда на прямых ВА' и АВ' лежат стороны квадрата. Дальнейшее продолжение не вызывает трудностей, предлагаем провести самим.

5. Метод подобия (гомотетии).

Сущность метода строят фигуру, подобную данной, не учитывая какой-нибудь линейный размер или специальное положение искомой фигуры относительно данных. Затем строят искомую (чаще всего гомотетией), учитывая, что коэффициент подобия равен отношению любых двух соответственных отрезков.

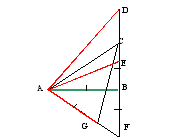
Задача. Даны угол и точка внутри него. Построить окружность, проходящую через точку А и касающуюся сторон угла.

Анализ. Центр искомой окружности должен лежать на биссектрисе данного угла. Снимем требование, чтобы окружность ω проходила через А (это подобно тому, что не требуется, чтобы расстояние от точки О до точки окружности равнялось известному отрезку а). Тогда легко построить окружность ω₁ , касающуюся сторон утла. Окружности ω и ω₁ гомотетичы (с центром в точке 0). Найдем образы точек А и В: А → А', В→В' . Очевидно, АВ׀׀А'В'.

Учитывая оказанное, можно наметить следующий план решения:

1) строим окружность СО₁ , касающуюся сторон угла;

2) проводам ОА;

3) строим точки пересечения ω и ω₁;

4) из точки А проводим прямую, параллельную прямой А'В'. Пусть В - одна из точек пересечения.

Построение и доказательство опускаем (самим).

Исследование. 1.Окружность ω₁ можно построить и бесчисленным множеством способов.

2. Пересечением ОА и ω₁ всегда являются две точки А' и А".

3. Через точку А можно провести две прямые, параллельные соответственно В'А' или В'А''. Эти две прямые l₁ и l₂ различны, если А ОВ'; и совпадает, если АОВ'.

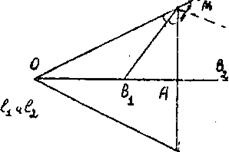
4. Пересечения l₁ ∩ ОВ и l₂ ∩ ОВ' существуют и единственны, если А ОВ' , т.е. задача в этом случае имеет два решения.

Если же А ОВ', то этим способом центр искомой окружности не найдем. Для этого принципиально нового случая найдем новое специфичное решение: строим прямую, перпендикулярную ОА-биссектрисе данного угла. Далее проведем биссектрисы углов ОСА и МСА. Точки в₁ и в₂ - искомые центры.

Задача (наглядная). Построить треугольник по двум углам , β

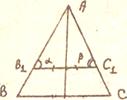
и медиане, проведенной из какой-нибудь вершины.

1. Строим треугольник АВ₁С₁

2. Подобным преобразованием получим искомый ΔАBC

6. Метод инверсии

Сущность метода: наряду с данными и искомыми фигурами рассматривают фигуры, инверсные им или их частям. Он применяется в тех случаях, когда построение фигуры, инверсной искомой, является более легкой (доступной). Построив инверсную построенной, получают искомую. Метод инверсии дает возможность решить трудные конструктивные задачи. Недостаток - громоздкость (большое число построений).

Задача. Даны: точка О и прямые а и в, не проходящие через О. Построить луч, выходящий из О, чтобы произведение его отрезков от О до точек пересечения с данными прямыми было равно ², где  - длина отрезка .

Анализ. Пусть [ОА) - искомый луч. Тогда ОА*ОВ= ². Инверсия I относительно окружности ω(o,r) точку B переведет в точку A, прямую в→в', где b' - некоторая окружноcть, тогда A = a∩в'.

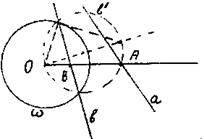
Построение. Строим последовательно: 1) ω(o,r); 2) в', где в' = I (в) окружность, проходящая через О; 3) А, А а ∩ в; 4) [ОА) - искомый.

Доказательство. Через В обозначим пересечение в ∩ [ОА). Тогда В – прообраз А, т.к. А = [ОА) ∩ в'→[ОА) ∩ в = В. По определению инверсии имеем: ОА*ОВ = r².

Исследование. Если: a ∩ в' = Ø, то нет решения; - точка касания, то одно решение; a ∩ в' = {A}, A – точка касания, то одно решение; a ∩ в' = {A₁ A₂, A₁ ≠ A₂, то два решения.

Алгебраический метод.

Сущность: решение задачи сводят к построению отрезка, длину которого можно выразить через длины данных отрезков с помощью формул. Затем строят искомый отрезок по полученной формуле.

Задача. Даны: угол АОВ и две точки С и D да луче OВ. Найти на луче [ОА) точку X, чтобы величина угла СХD была наибольшей.

Анализ. Пусть точка X найдена. Очевидно, точка X является точкой касания окружности, проходящей через С и D. Обозначим длину отрезка ОХ через х.

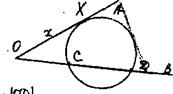
Имеем:

х² = |ОС|*|ОD|, |ОС| и |ОD | -

длины известных отрезков ОС и ОD) . План решения состоит из двух шагов: Строим так, чтобы

и х = [OA) ∩ω(O,x),

где – длина отрезка х.

Построение, доказательство, исследование предлагаем провести самим.

Построение отрезков, заданных формулами.

Алгебраический метод решения задач на построение сводится к построению отрезков, заданных формулами.

Полная формулировка задачи: даны отрезки . Пусть а, в, с,…, d – их длина при некоторой единице измерения. Требуется построить с помощью данных инструментов (циркуля и линейки) отрезок  , длина которого x (при той же единице измерения) выражается через длины данных отрезков формулой х = f (a, в², с,…, d). Будем рассматривать такие значения а, в, с,…,d, при которых f имеет смысл и положительна.

Мы уже знаем, как cтроить выражения

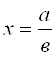,  , , , х = а ± в,(а - в, при а >

в). К рассмотренным построениям можно свести построение более сложных формул:

1) , n = натуральное число; делается так:

, причем , если n = p·q,

, если n = p² ± q²;

2)

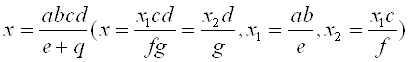
3)  · и т.д.

Все построенные выше формулы обладают одним общим cвойcтвом: они являютcя однородными выражениями первой степени. Напоминаем, выражение F(а,…,с) называют однородным степени 11, если

F(ta,…,tc) = tⁿ · F (a,…,c).

Пользуясь понятием однородной функции, мо;но выделить некоторые, классы алгебраичеcких выражений, которые могут быть построены циркулем и линейкой. Например, циркулем и линейкой можно построить:

1)  Oтрезок, заданный формулой

,

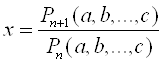где P_n+1 (…) и P_n(a,b,…,c) - однородные многочлены с рациональными коэффициентами от длин а,в,…,с отрезков степени соответственно n+1 и n.

Пусть

P_n+1 =

Далее, пусть  - произвольный отрезок, d - его длина (в той же единице измерения).

Разделим чиcлитель на dⁿ , знаменатель – на d^n-1 .

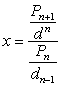
Выражение  представляет сумму одночленов вида .

Следовательно, можно построить каждое слагаемое, а потому и весь числитель: 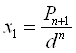. Аналогично,  . Наконец строим - отрезок длины х, где ;

2) отрезок, заданный формулой , где – ((…) – однородная рациональная функция 2 степени с рациональными коэффициентами. Делается так: , где (R₂(…) - отношение двух однородных многочленов , тогда 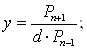 как и выше, строим

3) Замечание. При вычерчивании кривых иногда приходится строить алгебраические выражения, не являющиеся однородными первой степени. Пусть надо построить отрезок , длина которого x = f(a,b,…,c), где f(…) не является однородной первой cтепени, например, y = x³ +1.

Правило: построение произвольного выражения от n аргументов всегда можно свести к построению некоторого однородного выражения первой степени от n+1 аргументов. Достигается это выбором единицы измерения.

Выберем некоторый отрезок в качестве единичного, e =1.

- однородная функция первой степени.

Если сумеем построить отрезок  по этой формуле, то он и будет искомым при выбранной, единице масштаба. Ясно, что получим различные неравные отрезки в зависимости от выбора .

Примеры:

1)

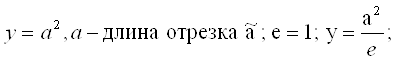
2)

3)

4)

5)

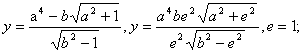
Разрешимость задач на построение с помощью циркуля и линейки.

Для краткости операции «+», «-», «·», «:» и извлечение арифметического квадратного корня» назовем основными действиями.

Теорема. Отрезок, длина которого задается положительной функцией для данных отрезков, может быть построен циркулем и линейкой тогда и только тогда, когда длина искомого отрезка выражается через длины данных отрезков при помощи конечного числа основных действий.

Достаточность. С помощью циркуля и линейки можно построить отрезок , длина которого x равна соответственно:

а+в

а-в

ав (за счет , е = 1)

 (- « -)

Так, как по условию длина искомого отрезка выражается через длины данных отрезков с помощью конечного числа основных действий, то остается единственный возможный случай, когда промежуточный отрезок не сможем построить - это построение разности а-в при а < в.

В таких случаях перейдем к положительной разности с помощью тождества а - в = - (в - а).

Теперь можно последовательно выполнить все построения, соответствующие основным операциям, и через конечное число шагов получим искомый отрезок.

Необходимость. Ясно, что построение отрезка  равносилъно построению его концов. Так как можно построить, то существует конечная последовательность основных построений, в результате выполнения которых на каком-то m -м шаге будет построен один конец (обозначим его через А ), а на к -ом - другой конец (точку в ). На плоскости построим прямоугольную декартовую систему координат.

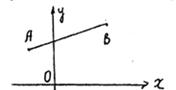
Пусть А (,β), В (γ, δ) - координаты построенных точек. Данные отрезки построим на положительной полуоси ОХ, тогда длины этих отрезков выражаются числами а₁,…,а_р ς (А, В) = х =  т.е. длина отрезка выражается через числа , β, γ, δ с помощью конечного числа основных действий. Если докажем, что сами числа , β, γ, δ выражаются через а₁,…,а_р с помощью конечного числа основных действий, то теорема будет доказана (длина отрезка выражается с помощью конечного числа основных действий).

Заметим, что любые построенные точки в ходе построения появляются двояко: либо выбираемые произвольно, либо как общие точки двух ранее построенных линий.

В первом случае выберем только такие точки, координаты которых выражаются через а₁,…,а_р при помощи конечного числа основных действий.

Во втором случае точка получается одним из следующих способов:

а) пересечение прямых (причем каждая прямая проведена через 2 построенные точки):

б) пересечение окружности и прямой (окружность построена через 2 построенные точки);

в) пересечение двух окружностей.

Рассмотрим случай а). Пусть прямая l₁ проведена через точки

C1 (x₁,y₁) и D₁ (x₂,y_2.). Покажем, что числа х₁, у₁, х₂ и у₂ могут быть выражены через а₁,…,а_р с помощью конечного числа основных действий (К4ОД). Действительно, пусть уравнение прямой l₁ имеет вид:

в₁х + с₁у = d₁

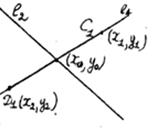
Легко убедиться, что чиcла в₁,с_1, d₁ выражаются через х_1, х_2, у_1, у₂ с помощью конечного числа основных действий. То же самое имеет место относительно коэффициентов прямой l₂ : в₂х + с₂у + d₂=0.

Точка пересечения (x₀, y₀) еcть решение cиcтемы

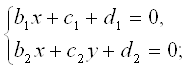
причем решение выражается через в₁, с₁,…, d₁ с помощью КrОД

В cлучае б) (х₀, у₀).- точка пересечения - есть решение системы

Числа х₀,у₀ выражаются через в,с, d, х₁, х_2, R c помощью КrОД.

В случае в) точка пересечения (х₀,у₀) является решением системы

Легко убедиться, что решение выражается с помощью КrОД через координаты ранее построенных точек.

Итак, координаты вновь построенных точек получаются через координаты ранее построенных с помощью конечного числа основных действий. Но, к ранее построенным точкам применимы точно такие же рассуждения. В конечном счете (из-за конечности числа построений циркулем и линейкой) получим, что координаты А и В выражаются через а₁,…,а_р с помощью КrОД.

Следствие. Если даны: отрезок, принимаемый за единичный, и число а, то отрезок длины а может быть построен циркулем и линейкой тогда и только тогда, когда число а может быть получено из «I» посредством лишь конечного числа основных действий.

О задачах, не разрешимых циркулем и линейкой.

Большой интерес представляют такие задачи на построения, когда фигура, удовлетворяющая всем условиям задачи, заведомо существует, но не может быть построена указанными инструментами. Такого рода "доказательства невозможности" даже простых по формулировке задач на построение часто оказываются связанными с наиболее трудными вопросами алгебры, анализа.

Познакомимся с некоторыми классическими задачами на построение, решения которых не могут быть найдены о помощью циркуля и линейки.