Навигация
Задача о квадратуре круга (пользовалась исключительной известностью с древнейших времен)
1. Задача о квадратуре круга (пользовалась исключительной известностью с древнейших времен).
Построить циркулем и линейкой квадрат, площадь которого бала бы равна площади круга данного радиуса.
Пусть ![]() - радиус круга,
- радиус круга, 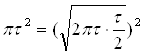 , т.е. площадь крута равна площади квадрата со стороной
, т.е. площадь крута равна площади квадрата со стороной![]() Иначе говоря, x является средней пропорциональной
Иначе говоря, x является средней пропорциональной ![]() и
и ![]() .
.
Если бы можно было построить ![]() , то легко можно было строить искомый квадрат.
, то легко можно было строить искомый квадрат.
Итак, задача о квадратуре круга свелась к задаче о опрямлении окружности, т.е. построению отрезка длины ![]() . При
. При ![]() эта длина равна
эта длина равна ![]() .
.
Ламберт И. (швейцарский математик) доказал, что π - иррациональное число. Но вопрос о возможности спрямления окружности остался открытым, так как согласно следствию из предыдущей теоремы отрезок длины а (при выбранном единичном отрезке) может быть построен циркулем и линейкой, если а получается из I с помощью конечного числа основных действий. Такие числа являются алгебраическими, т.е. служат корнями многочленов с рациональными коэффициентами. Числа, не являющиеся алгебраическими, называются трансцендентными.
В 1882 г. Линдеманн Ф. доказал, что π является трансцендентным числом. Следовательно, проблема о квадратуре крута разрешена, задача о квадратуре крута не разрешима о помощью циркуля и линейки.
2. Задачу удвоения куба: зная ребро куба, построить ребро куба, объем которого был бы вдвое больше объема данного.
Пусть а - длина ребра данного куба, x - искомого. Имеем: х2 = 2а3. Если а = 1, то получим уравнение х3 – 2 = 0. Это уравнение не имеет рациональных корней (т.к. рациональные корни этого уравнения обязательно целые, их надо искать среди делителей свободного члена). Из алгебры известно: если уравнение ![]() рациональные числа) не имеет рационального корня, то ни один корень этого уравнения не может быть выражен через I лишь с помощью конечного числа основных действий. Тогда, учитывая указанное выше следствие, получим, что отрезок длины x не может быть построен с помощью циркуля и линейки.
рациональные числа) не имеет рационального корня, то ни один корень этого уравнения не может быть выражен через I лишь с помощью конечного числа основных действий. Тогда, учитывая указанное выше следствие, получим, что отрезок длины x не может быть построен с помощью циркуля и линейки.
Замечание. Эта задача может быть решена с привлечением двух прямых углов.
3. Задача о трисекции угла: построить угол, в 3 раза меньший данного.
Достаточно рассмотреть эту задачу для острых углов, т.к. при тупом ![]() угол
угол ![]()
![]() является острым и третья часть равна
является острым и третья часть равна ![]() Отсюда следует, что
Отсюда следует, что![]()
Итак, пусть α - данный острый угол, φ - искомый,
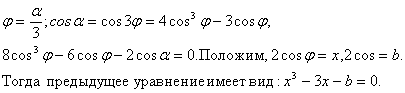

Если отрезок длины x можно построить циркулем и линейкой, то из прямоугольника следует, что можно построить и сам угол φ. Следовательно, задача свелась к построению отрезка длины х, где x - один из корней уравнения (I).
Пусть α = 60º, тогда в = 1. Уравнение (I) приводится к виду:
![]()
Легко убедиться (из тех же соображений, что и выше), что у этого уравнения нет рациональных корней, следовательно нет ни одного корня, который выражался бы через I с помощью конечного числа основных действий.
Следовательно, задача о трисекции угла не разрешима циркулем и линейкой в общем виде.
Но, может быть, она никогда не разрешима? Это не так. Пусть α = 90°. Тогда уравнение (I) имеет вид: x3 - зх = 0, ![]() Отрезок
Отрезок ![]() можно построить, следовательно, задача в этом случае разрешима.
можно построить, следовательно, задача в этом случае разрешима.
|
нетрудно построить и угол φ. | Можно чисто геометрически построить угол в 60° (хорда равна радиусу, см.рис.).
|
Замечание 1. Существуют приборы-трисекторы, позволяющие делить угол на три равные части.

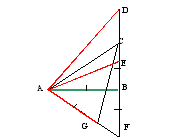
АВСD и AB1C1D1 - ромбы, φ =![]() .
.

Замечание 2. Задачу о трисекции угла легко решить циркулем. Строим последовательно: 1) окружность ω![]() расстояние между отметками на линейке;
расстояние между отметками на линейке;
2) точку А;
3) прямую, проходящую через А так, чтобы расстояние между второй точкой пересечения с окружностью и точкой пересечения этой прямой с прямой ОN было равно ![]() .
.
Решение проблемы связано большими трудностями, и решена она полностью великим немецким математиком Гауссом в 1796 году.
Вопрос построения правильного n -угольника равносилен вопросу о возможности деления окружности на n равных частей. Возьмем окружноcть радиуcа ![]() и прямоугольную систему координат. Задача деления
и прямоугольную систему координат. Задача деления
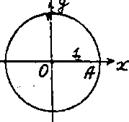
окружности на n равных частей состоит в построении точек

т.е, в построении корней уравнения Zn– 1= 0 о тличных – от Z0 = 1. Это равносильно построению корней уравнения ![]() Это уравнение называется уравнением деления окружности.
Это уравнение называется уравнением деления окружности.
Гаусс доказал следующую замечательную теорему.
Теорема. Построение правильного n - угольника с помощью циркуля и линейки возможно тогда и только тогда, когда ![]() (числа Ферма).
(числа Ферма).
Рассмотрим несколько частных случаев:
|
|
Пусть |
Следовательно, правильный пятиугольник можно построить циркулем и линейкой.
Подставим:
![]()
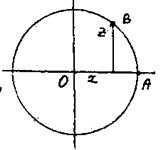
Строим ![]() , потом
, потом ![]() Повторяя дугу АВ 3 раза, получим все точки.
Повторяя дугу АВ 3 раза, получим все точки.
Построения иными инструментами
Похожие работы
... документации немалая роль отводится чертежнику-конструктору. Он выполняет рабочие чертежи отдельных деталей по чертежу общего вида изделия(при этом используются геометрические построения),разработанного конструктором, предопределяет технологию изготовления отдельных деталей в зависимости от наличия на предприятии технологического оборудования, отрабатывает конструкции деталей на технологичность и ...
... развитие логического мышления учащихся является одной из основных целей курса геометрии. При изучении геометрии развитие логического мышления учащихся осуществляется в процессе формирования понятий, доказательства теорем, решения задач. При изучении геометрических построений, прежде всего, приходится преодолевать трудности логического порядка. В условиях школы для преодоления этих трудностей ...
... прямых и т.д.; углубить имеющиеся знания по геометрии. Гипотеза: мы предполагаем, что сможем решить некоторые геометрические задачи на построение, используя не классический набор инструментов (циркуль и линейку), а набор из циркуля и короткой градуированной веревки. Задачи о построении на местности Геометрия зародилась в глубокой древности, она изучает форму и взаимное расположение фигур в ...
... расстояния между точками довольно велики и нет таких линеек и циркулей, которые могли бы помочь нам. Да и вообще чертить на земле какие-либо линии затруднительно. Таким образом, построения на местности, основываясь на геометрических законах, имеют свою специфику: Во – первых, все прямые не проводятся на земле, а прокладываются, т. е. отмечается на них, например, колышками, достаточно густая сеть ...
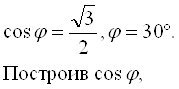








0 комментариев