Навигация
Основные параметры интегральных микросхем
1.1. Основные параметры интегральных микросхем
Плотность упаковки – это число элементов электронной схемы в одном кубическом сантиметре объема интегральной микросхемы.
Степень интеграции x определяется количеством элементов n, вхо- дящих в состав интегральной микросхемы.
x = lg n
Микросхема 1 степени интеграции содержит до 10 элементов (мало- масштабная интегральная схема – мис). Микросхема 2 степени интеграции (среднемасштабная – сис) содержит от 10 до 100 элементов. Микросхема 3 степени интеграции содержит от 10² до 10³ элементов и относится к катего-рии больших интегральных микросхем (БИС). Сверхбольшие (СБИС) имеют
степень интеграции более 1000 элементов (табл. 1).
Таблица 1
| Уровень сложности ИС | Количество интегрированных элементов | Параметры функционального назначения ИС |
| МИС | ≤ 10 | Биполярные ячейки, простые логические элементы, дифференциальные усилительные каскады |
| СИС | 10 – 100 | Триггеры, регистры, сумматоры, операцион- ные усилители, коммутаторы |
| БИС | 100 – 1000 | Полупроводниковые запоминающие и ариф- метико-логические устройства |
| СБИС | > 1000 | Микропроцессоры, однокристальные микро- ЭВМ, аналого-цифровые преобразователи |
1.2. Серии и семейства серий интегральных схем
Серия – это комплект из нескольких типов интегральных схем, имею- щих единое конструктивно-технологическое исполнение и предназначен- ных для совместного применения в аппаратуре. Интегральные схемы, входя- щие в серию, имеют единые эксплутационные показатели и используются как совместимые наборы деталей, пригодные для создания электронной ап- паратуры любой степени сложности.
Серии интегральных схем, совместимые друг с другом по логическим
уровням, условиям эксплуатации и конструктивным показателям, могут образовывать семейства серий интегральных схем.
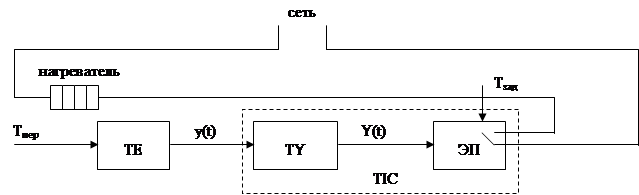
2. ЛОГИЧЕСКИЕ ЭЛЕМЕНТЫ
Логические и запоминающие элементы составляют основу устройств цифровой обработки информации – вычислительных машин, цифровых измерительных приборов и устройств автоматики. Логические элементы выполняют простейшие логические операции над цифровой информацией: преобразуют по определенным правилам входную информацию в выход-ную. Операции, используемые при обработке цифровой информации, осно-ваны на двоичной системе счисления, представляющей информацию в виде слов – комбинаций символов 1 и 0.
Обработка цифровой информации логическими элементами произво-дится по законам и правилам алгебры логики, разработанной в XIX веке английским ученым Дж. Булем.
Логические преобразования двоичных сигналов включают три элементарные операции:
1. логическое сложение (дизъюнкцию) или операцию ИЛИ
F=x1+x2+…+xn
2. логическое умножение (конъюкцию) или операцию И
F= x1 · x2·…·xn
2. логическое отрицание (инверсию) или операцию НЕ
F= x
Определение этих операций дается с помощью таблиц истинности, содержащих перечисление всех возможных сочетаний (наборов) входных переменных (входных слов).
Каждая простая логическая функция может быть технически реализо- вана простыми элементами, к которым относятся элементы И, ИЛИ, НЕ и их комбинации.
На рис. 3 приведены условные обозначения логических элементов и таблицы истинности.
Из простых элементов можно составить сколь угодно сложные логи-ческие устройства, например, счетчики импульсов, регистры, сумматоры, блоки памяти и т.п.
На практике применяют комбинированные элементы, реализующие две логические операции, например, элементы И-НЕ и ИЛИ-НЕ. Они назы-ваются функционально полными, т.к. позволяют реализовать любую логи-ческую функцию. Например, имея набор элементов И-НЕ можно построить схему ИЛИ.
| Наименование функции | Условное графи- ческое обозначение | Выражение функции | Таблицы истинности | ||||
| x1 | 0 | 0 | 1 | 1 | |||
| x2 | 0 | 1 | 0 | 1 | |||
| ИЛИ | y= x1+x2 | y | 0 | 1 | 1 | 1 | |
| И |
y= x1 ·x2 | y | 0 | 0 | 0 | 1 | |
| НЕ | _ y= x1 | y | 1 | 1 | 1 | 0 | |
| ИЛИ-НЕ | ___ y= x1+x2 |
y | 1 | 0 | 0 | 0 | |
| И-НЕ | ____ y= x1 ·x2 |
y | 1 | 1 | 1 | 0 | |
Рис. 3
Элемент И-НЕ (штрих Щеффера) выполняет операцию
___________
F= x1 · x2 · x3 ·…· xn
Элемент ИЛИ-НЕ (стрелка Пирса) выполняет операцию
_____________
F=x1+x2+ x3+…+xn
Примеры использования функционально полных элементов сведены в таблице 2, где показано, как набором элементов И/-НЕ можно реализовы- вать функции И, ИЛИ, НЕ.
Таблица 2
| Элемент | Логические операции | ||
| НЕ | И | ИЛИ | |
|
И-НЕ |
y1=x=x ·x
т. к. x ·x ·x ·…=x | y2=x1 ·x2= x1 ·x2
т. к. x= x | y3= x1 +x2= x1 · x2
т. к. x1 ·x2= x1 +x2 - теорема де Моргана |
Реализация логических устройств на базе комбинированных элементов упрощает компановку и ремонт устройств.
Похожие работы
... электротехнических и электронных устройств, в которых используется явление резонанса напряжения. Литература 1. Иванов И.И., Равдоник В.С. Электротехника. - М.: Высшая школа, 1984, с.53 - 58. 2. Касаткин А.С., Немцов М.В. Электротехника. - М.: Энергоатомиздат, 1983, с.73 - 77. Лабораторная работа №5 КОМПЕНСАЦИЯ РЕАКТИВНОЙ МОЩНОСТИ Цель работы. Ознакомление с методом повышения ...
... и электрические измерения * * * 4.2. Содержание разделов дисциплины Введение Электрическая энергия, особенности ее производства, распределения и области применения. Роль электротехники и электроники в развитии автоматизации производственных процессов и систем управления. Значение электротехнической подготовки для бакалавров и инженеров неэлектротехнических направлений. Связь со ...
ния и тока Uнср Iн ср. 2. Среднюю мощность нагрузочного устройства Рн ср. 3. Амплитуду основной гармоники выпрямленного напряжения U ОСН m. 4. Коэффициент пульсаций р выпрямленного напряжения. 5. Действующее значение тока нагрузки I. 6. Полную мощность S источника питания. 7. Активную мощность Р в сопротивлении нагрузки. 8. Коэффициент мощности выпрямителя. Дано: U=40 В, ...
... Теоретические основы электротехники. Изд. 4-е, перераб. и доп. Учебник для энергетич. и электротехнич. специальностей техникумов. М. «Высш. Школа», 1975. 496 с. с ил.3. Данилов И.А., Иванов П.М. Общая электротехника с основами электроники Уч. Пособие для студентов неэлектрических специальностей, средн. специальных уч. Заведений изд. 3-е.-М.: «Высш. Школа», 1998. 752 с. ил.4. Китунович Ф.Г. ...


0 комментариев