Навигация
Эквивалентные преобразования пассивных участков электрической цепи
11 Эквивалентные преобразования пассивных участков электрической цепи
В зависимости от назначении электрической цепи, её элементы могут соединяться между собой последовательно, параллельно, последовательно – параллельно (по смешанной схеме), треугольником или звездой.
Последовательным называют соединение при котором ток в каждом элементе один и тот же. При таком соединении “n” резисторов (рис. 1.8а) могут быть заменены одним резистором (рис. 1.8б) с эквивалентным сопротивлением Rэ, при котором ток I в обоих схемах будет одинаков (при равенстве напряжения U на входах схем).
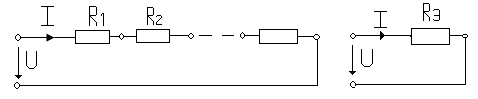
а) б)
рис. 1.8
Для схемы рис. 1.8а)
![]() ,
,
а для схемы рис. 1.8б)
![]()
Таким образом (из равенства напряжений на входах) получаем, что:
![]() (1.1.19)
(1.1.19)
Эквивалентное сопротивление последовательного соединения резисторов равно сумме сопротивлений этих резисторов.
Параллельным называют соединение при котором все участки цепи присоединяются к одной паре узлов, т.е. находятся под воздействием одного и того же напряжения. При таком соединении рис. 1.9а) “n” параллельных резисторов можно заменить одним эквивалентным рис. 1.9б) сопротивление RЭ которое обеспечивает равенство токов I.
В неразветвлённых участках цепи:
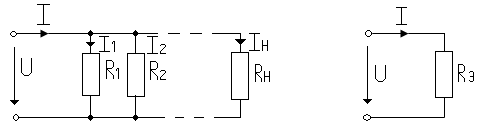
Рис.1.9.
Для схемы рис.1.9(а) по первому закону Кирхгофа можно записать:
![]()
Так как для каждой ветви по закону Ома
![]() ,то :
,то :
![]() , или
, или
![]() (1.1.20)
(1.1.20)
Поскольку
![]() ;
; ![]() ;
; ![]() ,…
,…![]() ,
,
То окончательно получаем:
![]() (1.1.21)
(1.1.21)
Эквивалентная проводимость параллельно соединённых резистивных элементов равна сумме проводимостей этих элементов.
Из (1.20) следует, что при параллельном соединении двух резисторов их общее (эквивалентное) сопротивление равно:
![]() (1.1.22)
(1.1.22)
Токи I1 и I2 двух параллельных ветвей выражаются через ток I в неразветвлённом участке цепи рис.1.10 формулами:
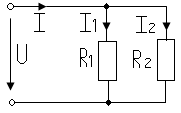
Рис.1.10
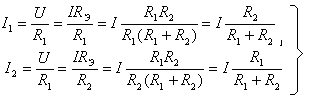 (1.1.23)
(1.1.23)
Сопротивления (1.1.23) называют формулами и разброса токов. Они могут быть получены также из системы уравнений:
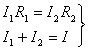 (1.1.24)
(1.1.24)
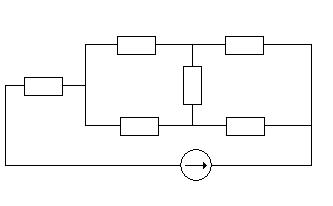
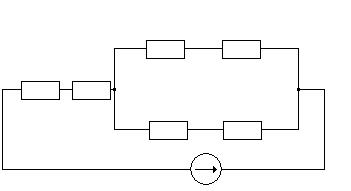
Смешанное (последовательно-параллельное) соединение резистивных элементов приведено на рис.1.11
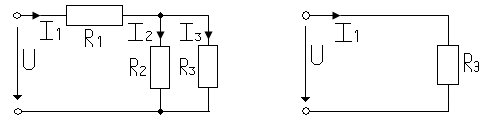
Рис.1.11
Из рис. 1.11 следует, что величина электрического сопротивления ,при котором ток в обоих схемах одинаков, равна :
![]() (1.1.25)
(1.1.25)
Соединение треугольником и звездой .
В некоторых электрических цепях встречаются соединения элементов, которые нельзя отнести ни к одному из выше рассмотренных. Пример такой цепи приведён на рис.1.22(а):
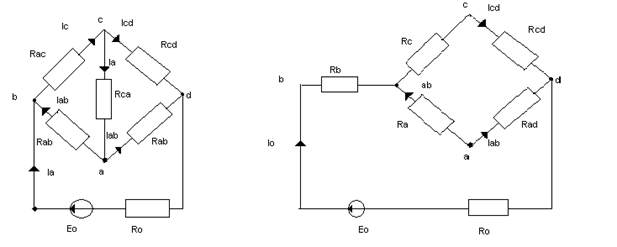
а) б)
рис.1.12
Резисторы Rab, Rbc и Rcd на рис.1.12(а) соединены треугольником, а на рис. 1.22 (б) резисторы Ra, Rb, Rc - соединены звездой. Схема рис.1.12(б) проще для расчёта,чем схема рис.1.12(а),поэтому следует получить выражение Ra, Rb, Rc через Rab, Rbc, Rca и наоборот.
При эквивалентной замене обоих схем, токи Ia, Iab, Icd равны и, следовательно, равны напряжения Uab, Ubc, Ucd.
Запишем уравнение по второму закону Кирхгофа для треугольника abc рис.1.12(а):
![]() (1.1.26)
(1.1.26)
Для узлов a и b в треугольнике по первому закону Кирхгофа:
![]() ,
, ![]() (1.1.27)
(1.1.27)
Подставив (1.27) в (1.26),получим:
![]() (1.1.28)
(1.1.28)
Для звезды рис.1.12 (б):
![]() (1.1.29)
(1.1.29)
Из сравнения (1.28) с (1.29) следует, что:
![]() ;
; ![]() (1.1.30)
(1.1.30)
По аналогии можно получить, что:
![]() (1.1.31)
(1.1.31)
Формулы (1.30) И (1.31) позволяют преобразовать треугольник сопротивлений в эквивалентную звезду сопротивлений.
Формулы обратного перехода звезды сопротивлений в треугольник сопротивлений можно получить заменив в формулах (1.30) и (1.31) все сопротивления проводимостями. При этом получим:
![]() ;
; ![]() ;
; ![]() (1.1.32)
(1.1.32)
Переходя к сопротивлениям, получим:
![]() ;
; ![]() ;
; ![]() ; (1.1.33)
; (1.1.33)
Похожие работы
... неровностей на поверхности анода, т.е. происходит его полировка. 2 Расчётная часть 2.1Задание на курсовую работу Расчет разветвлённой электрической цепи постоянного тока. Для заданной электрической цепи необходимо: 1) Записать систему уравнений по законам Кирхгофа (без расчетов); 2) Определить все токи и ...
чает в себя источники мощности (активные элементы) и приемники (пассивные элементы). В качестве пассивного линейного элемента в цепях постоянного тока выступает резистор, имеющий электрическое сопротивление R. Единица измерения Ом. Величина, обратная сопротивлению, называется электрической проводимостью: G = 1/R. Единица измерения См - сименс. В качестве активных элементов - источников ...
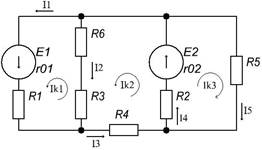
... будущего специалиста к работе на производстве. 1. Анализ электрического состояния линейных электрических цепей постоянного тока Схема электрической цепи постоянного тока: R2 I2 R7 I5 E1,r02 I7 R1 I3 R5 R3 R4 I4 I6 I1 E2,r02 R6 Рис.1.0 ...
... контура в той последовательности, в которой производим обход контура, прикладывая сопротивления друг к другу, по оси ординат - потенциалы точек с учетом их знака. рис.1.7 1.2 Расчет нелинейных электрических цепей постоянного тока Построить входную вольтамперную характеристику схемы (рис.1.8) Определить токи во всех ветвях схемы и напряжения на отдельных элементах, используя полученные ...
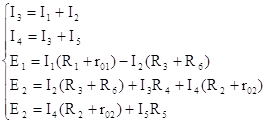

0 комментариев