Навигация
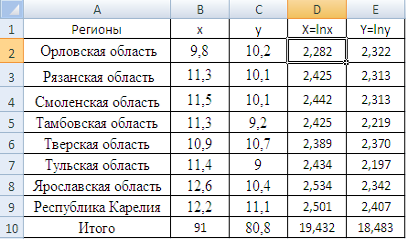
Значения парных коэффициентов корреляции найдем из соответствующей матрицы
3. Значения парных коэффициентов корреляции найдем из соответствующей матрицы.
Таблица №10 Корреляционная матрица
| y | x1 | x2 | |
| y | 1 | ||
| x1 | 0,784786247 | 1 | |
| x2 | 0,60206001 | 0,531178469 | 1 |
По величине парных коэффициентов корреляции может обнаруживаться лишь явная коллинеарность факторов. Наибольшие трудности в использовании аппарата множественной регрессии возникают при наличии мультиколлинеарности факторов, когда более чем два фактора связаны между собой линейной зависимостью, т.е. имеет место совокупное воздействие факторов друг на друга.
Наличие мультиколлинеарности факторов может означать, что некоторые факторы будут всегда действовать в унисон. В результате вариация в исходных данных перестает быть полностью независимой и нельзя оценить воздействие каждого фактора в отдельности. Чем сильнее мультиколлинеарность факторов, тем менее надежна оценка распределения суммы объясненной вариации по отдельным факторам с помощью метода наименьших квадратов (МНК).
Частные коэффициенты корреляции найдем по формулам
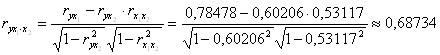 ,
,
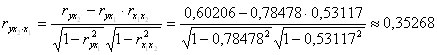 ,
,
их значения показывают, что при отсутствии влияния других факторов, связь с рассматриваемым фактором усиливается т.е. мультиколлинеарность между ними существует.
4. Рассчитаем прогнозное значение результата, если прогнозные значения факторов составляют 110% их максимального значения. Найдем прогнозные значения факторов и подставим их в полученное уравнение регрессии.
По условию прогнозные значения составляют 110% их максимального значения.
Таблица №11
| maxX1 | maxX2 |
| 28 | 10 |
Далее вычисляем прогнозные значения факторов: ![]() . Затем, подставив эти значения в уравнение регрессии, получим прогнозное (предсказанное) значение фактора
. Затем, подставив эти значения в уравнение регрессии, получим прогнозное (предсказанное) значение фактора ![]() . Доверительный интервал прогноза оценивается формулой:
. Доверительный интервал прогноза оценивается формулой: ![]() , где
, где ![]() - ошибка прогноза,
- ошибка прогноза,![]() стандартная ошибка регрессии.
стандартная ошибка регрессии.
Таблица №12
| Стандартная ошибка | 1,104878833 |
![]() ;
;
![]() - коэффициент Стьюдента, который в данном случае имеет смысл кратности случайной (стандартной) ошибки прогноза
- коэффициент Стьюдента, который в данном случае имеет смысл кратности случайной (стандартной) ошибки прогноза ![]() ;
;
![]() - число, которое получим в результате операций над матрицами:
- число, которое получим в результате операций над матрицами:
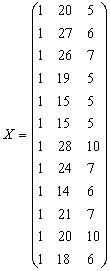 -
-
матрица значений факторных переменных ![]() ,
,
![]() транспонированная матрица
транспонированная матрица ![]() ;
;
![]() - произведение матриц
- произведение матриц ![]() ;
;
![]() - матрица, обратная к матрице
- матрица, обратная к матрице ![]() ;
;
![]() - матрица прогнозных значений факторов;
- матрица прогнозных значений факторов;
![]() - транспонированная матрица прогнозов.
- транспонированная матрица прогнозов.
Фактор ![]() представляет собой фиктивную переменную, которую необходимо ввести в уравнение регрессии для того, чтобы преобразовать его в "приведенную" форму вида
представляет собой фиктивную переменную, которую необходимо ввести в уравнение регрессии для того, чтобы преобразовать его в "приведенную" форму вида ![]() .
.

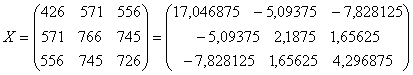
Максимальную ошибку прогноза ![]() =11,07714043: 1) нижняя граница прогноза
=11,07714043: 1) нижняя граница прогноза ![]() =44,92285957, 2) верхнюю границу прогноза
=44,92285957, 2) верхнюю границу прогноза ![]() =67,07714043. Интервал прогнозных значений результативного признака
=67,07714043. Интервал прогнозных значений результативного признака
![]() =>
=>![]()
Используя данные, представленные в таблице проверить наличие гетероскедастичности, применяя тест Голдфельда-Квандта.
Таблица№13. Данные
| Страна | Индекс человеческого развития, У | Расходы на конечное потребление в текущих ценах, % к ВВП, Х |
| Австрия | 0,904 | 75,5 |
| Австралия | 0,922 | 78,5 |
| Англия | 0,918 | 84,4 |
| Белоруссия | 0,763 | 78,4 |
| Бельгия | 0,923 | 77,7 |
| Германия | 0,906 | 75,9 |
| Дания | 0,905 | 76,0 |
| Индия | 0,545 | 67,5 |
| Испания | 0,894 | 78,2 |
| Италия | 0,900 | 78,1 |
| Канада | 0,932 | 78,6 |
| Казахстан | 0,740 | 84,0 |
| Китай | 0,701 | 59,2 |
| Латвия | 0,744 | 90,2 |
| Нидерланды | 0,921 | 72,8 |
| Норвегия | 0,927 | 67,7 |
| Польша | 0,802 | 82,6 |
| Россия | 0,747 | 74,4 |
| США | 0,927 | 83,3 |
| Украина | 0,721 | 83,7 |
| Финляндия | 0,913 | 73,8 |
| Франция | 0,918 | 79,2 |
| Чехия | 0,833 | 71,5 |
| Швейцария | 0,914 | 75,3 |
| Швеция | 0,923 | 79,0 |
1) Найдем параметры линейного уравнения множественной регрессии и значения остатков.
Определим остаточные суммы квадратов ![]() и
и ![]() , то есть суммы квадратов остатков регрессии по "урезанным выборкам".
, то есть суммы квадратов остатков регрессии по "урезанным выборкам".
Таблица№14
| № | Y | X | Yp | ei | (ei) ^2 | |
| 1 | 0,932 | 78,6 | 77,90431365 | 0,695686352 | 0,483979501 | |
| 2 | 0,927 | 67,7 | 77,85057558 | -10,15057558 | 103,0341846 | |
| 3 | 0,927 | 83,3 | 77,85057558 | 5,44942442 | 29,69622651 | |
| 4 | 0,923 | 77,7 | 77,80758513 | -0,107585125 | 0,011574559 | |
| 5 | 0,923 | 79,0 | 77,80758513 | 1, 192414875 | 1,421853234 | |
| 6 | 0,922 | 78,5 | 77,79683751 | 0,703162488 | 0,494437485 | |
| 7 | 0,921 | 72,8 | 77,7860899 | -4,986089898 | 24,86109247 | |
| 8 | 0,918 | 84,4 | 77,75384706 | 6,646152943 | 44,17134894 | S1 |
| 9 | 0,918 | 79,2 | 77,75384706 | 1,446152943 | 2,091358334 | 206,2660556 |
| 10 | 0,914 | 75,3 | 77,7108566 | -2,410856603 | 5,812229559 | |
| 11 | 0,913 | 73,8 | 77,70010899 | -3,900108989 | 15,21085013 | |
| 12 | 0,906 | 75,9 | 77,62487569 | -1,724875694 | 2,975196159 | |
| 13 | 0,905 | 76,0 | 77,61412808 | -1,61412808 | 2,60540946 | |
| 14 | 0,904 | 75,5 | 77,60338047 | -2,103380467 | 4,424209388 | |
| 15 | 0,900 | 78,1 | 77,56039001 | 0,539609988 | 0,291178939 | |
| 16 | 0,894 | 78,2 | 77,49590433 | 0,704095669 | 0,495750712 | |
| 17 | 0,833 | 71,5 | 76,8402999 | -5,3402999 | 28,51880303 | |
| 18 | 0,802 | 82,6 | 76,50712388 | 6,092876121 | 37,12313943 | |
| 19 | 0,763 | 78,4 | 76,08796695 | 2,312033052 | 5,345496834 | |
| 20 | 0,747 | 74,4 | 75,91600513 | -1,51600513 | 2,298271555 | |
| 21 | 0,744 | 90,2 | 75,88376229 | 14,31623771 | 204,9546622 | |
| 22 | 0,740 | 84,0 | 75,84077183 | 8,159228165 | 66,57300425 | |
| 23 | 0,721 | 83,7 | 75,63656718 | 8,063432824 | 65,0189489 | |
| 24 | 0,701 | 59,2 | 75,4216149 | -16,2216149 | 263,1407901 | S2 |
| 25 | 0,545 | 67,5 | 73,74498718 | -6,244987181 | 38,99986489 | 743,7878055 |
1) Находим наблюдаемое значение критерия ![]() . По условию задачи
. По условию задачи ![]() . Из таблицы значений
. Из таблицы значений ![]() Фишера находим, что
Фишера находим, что ![]()
Вывод: отвергаем нулевую гипотезу ![]() на принятом уровне значимости
на принятом уровне значимости ![]() , т.к. наблюдаемое значение критерия больше табличного.
, т.к. наблюдаемое значение критерия больше табличного.
Следовательно, предположение об однородности дисперсий ошибок, при условии, что выполнены стандартные предположения о модели наблюдений, включая предположение о нормальности ошибок, неверно. Наблюдается гетероскедастичность, что приводит к ошибочным статистическим выводам при использовании МНК. Следовательно, полученные оценки не являются состоятельными.
Задача № 4По данным таблицы построить уравнение регрессии, выявить наличие автокорреляции остатков, используя критерий Дарбина - Уотсона, и проанализировать пригодность полученного уравнения для построения прогнозов.
Таблица №15
| Год | Выпуск продукции в США в среднем за 1 час, % к уровню 1982 г., Х | Среднечасовая заработная плата в экономике США, в сопоставимых ценах 1982 г., Y |
| 1960 | 65,6 | 6,79 |
| 1961 | 68,1 | 6,88 |
| 1962 | 73,3 | 7,07 |
| 1963 | 76,5 | 7,17 |
| 1964 | 78,6 | 7,33 |
| 1965 | 81,0 | 7,52 |
| 1966 | 83,0 | 7,62 |
| 1967 | 85,4 | 7,72 |
| 1968 | 85,9 | 7,89 |
| 1969 | 85,9 | 7,98 |
| 1970 | 87,0 | 8,03 |
| 1971 | 90,2 | 8,21 |
| 1972 | 92,6 | 8,53 |
| 1973 | 95,0 | 8,55 |
| 1974 | 93,3 | 8,28 |
| 1975 | 95,5 | 8,12 |
Найдем параметры линейного уравнения множественной регрессии и значения остатков.
Дополним таблицу данных столбцами "![]() ", "Квадрат разности остатков
", "Квадрат разности остатков ![]() " и "Квадрат остатка
" и "Квадрат остатка ![]() " и заполним их.
" и заполним их.
Таблица №16
| Y | X | Yi | et | et-1 | (et-et-1) ^2 | et^2 |
| 6,79 | 65,6 | 6,667235239 | 0,122765 | 0,015071 | ||
| 6,88 | 68,1 | 6,815288112 | 0,064712 | 0,122765 | 0,003370136 | 0,004188 |
| 7,07 | 73,3 | 7,123238088 | -0,05324 | 0,064712 | 0,013912197 | 0,002834 |
| 7,17 | 76,5 | 7,312745766 | -0,14275 | -0,05324 | 0,008011624 | 0,020376 |
| 7,33 | 78,6 | 7,437110179 | -0,10711 | -0,14275 | 0,001269895 | 0,011473 |
| 7,52 | 81,0 | 7,579240937 | -0,05924 | -0,10711 | 0,002291464 | 0,003509 |
| 7,62 | 83,0 | 7,697683236 | -0,07768 | -0,05924 | 0,000340118 | 0,006035 |
| 7,72 | 85,4 | 7,839813994 | -0,11981 | -0,07768 | 0,001775001 | 0,014355 |
| 7,89 | 85,9 | 7,869424568 | 0,020575 | -0,11981 | 0,019709191 | 0,000423 |
| 7,98 | 85,9 | 7,869424568 | 0,110575 | 0,020575 | 0,008100000 | 0,012227 |
| 8,03 | 87,0 | 7,934567833 | 0,095432 | 0,110575 | 0,000229318 | 0,009107 |
| 8,21 | 90,2 | 8,12407551 | 0,085924 | 0,095432 | 0,000090396 | 0,007383 |
| 8,53 | 92,6 | 8,266206268 | 0,263794 | 0,085924 | 0,031637467 | 0,069587 |
| 8,55 | 95,0 | 8,408337026 | 0,141663 | 0,263794 | 0,014915922 | 0,020068 |
| 8,28 | 93,3 | 8,307661073 | -0,02766 | 0,141663 | 0,028670633 | 0,000765 |
| 8,12 | 95,5 | 8,437947601 | -0,31795 | -0,02766 | 0,084266268 | 0,101091 |
| Суммы | 0,218589631 | 0,298494 |
По формуле  вычислим значение статистики
вычислим значение статистики ![]() :
:
Так как ![]() , то значение статистики
, то значение статистики
равно ![]() .
.
По таблице критических точек Дарбина Уотсона определим значения критерия Дарбина-Уотсона ![]() (нижнее) и
(нижнее) и ![]() (верхнее) для заданного числа наблюдений
(верхнее) для заданного числа наблюдений ![]() , числа независимых переменных модели
, числа независимых переменных модели ![]() и уровня значимости
и уровня значимости ![]() . Итак, находим, что
. Итак, находим, что ![]() ,
, ![]() .
.
По этим значениям числовой промежуток ![]() разбиваем на пять отрезков:
разбиваем на пять отрезков:
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() .
.
На основании выполненных расчетов находим, что наблюдаемое значение статистики ![]() принадлежит первому интервалу.
принадлежит первому интервалу.
Вывод: существует отрицательная автокорреляция, то есть гипотеза ![]() отклоняется и с вероятностью
отклоняется и с вероятностью ![]() принимается гипотеза
принимается гипотеза ![]() .
.
Следовательно, полученное уравнение регрессии ![]() не может быть использовано для прогноза, так как в нем не устранена автокорреляция в остатках, которая может иметь разные причины. Автокорреляция в остатках может означать, что в уравнение не включен какой-либо существенный фактор. Возможно также, что форма связи неточна.
не может быть использовано для прогноза, так как в нем не устранена автокорреляция в остатках, которая может иметь разные причины. Автокорреляция в остатках может означать, что в уравнение не включен какой-либо существенный фактор. Возможно также, что форма связи неточна.
В таблице приводятся данные о динамике выпуска продукции Финляндии (млн. долл.).
Таблица №17
| Год | Выпуск продукции, yt млн.долл. |
| 1989 | 23 298 |
| 1990 | 26 570 |
| 1991 | 23 080 |
| 1992 | 29 800 |
| 1993 | 28 440 |
| 1994 | 29 658 |
| 1995 | 39 573 |
| 1996 | 38 435 |
| 1997 | 39 002 |
| 1998 | 39 020 |
| 1999 | 40 012 |
| 2000 | 41 005 |
| 2001 | 39 080 |
| 2002 | 42 680 |
Задание:
1. Постройте график временного ряда.
2. Сделайте вывод о присутствии или отсутствии тренда при доверительной вероятности 0,95.
3. Найдите среднее значение, среднеквадратическое отклонение и коэффициенты автокорреляции (для лагов ![]() ) заданного ВР.
) заданного ВР.
4. Проведите сглаживание данного ВР методом скользящих средних, используя простую среднюю арифметическую с интервалом сглаживания ![]() ;
;
5. Найдите уравнение тренда ВР ![]() , предполагая, что он линейный, и проверьте его значимость на уровне
, предполагая, что он линейный, и проверьте его значимость на уровне ![]() .
.
Похожие работы
... и детерминации и F-критериев Фишера наибольшие. 3. Множественная регрессия Цель работы – овладеть методикой построения линейных моделей множественной регрессии, оценки их существенности и значимости, расчетом показателей множественной регрессии и корреляции. Постановка задачи. По данным изучаемых регионов (таблица 1) изучить зависимость общего коэффициента рождаемости () от уровня бедности ...
... и все коэффициенты корреляции равны 1, то определитель такой матрицы равен 0: . Чем ближе к 0 определитель матрицы межфакторной корреляции, тем сильнее мультиколлинеарность факторов и ненадежнее результаты множественной регрессии. И наоборот, чем ближе к 1 определитель матрицы межфакторной корреляции, тем меньше мультиколлинеарность факторов. Проверка мультиколлинеарности факторов может быть ...
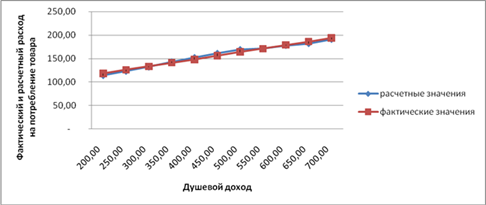
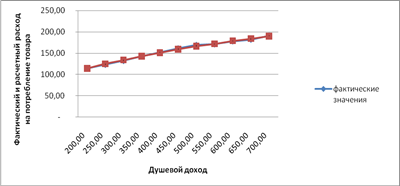
трех исследованных моделей. Отбор факторов и показателей для построения функции потребления Исходные данные, характеризующие изменение душевого дохода (Х) и расхода на потребление товара А (Y) приведены в таблице 1. Таблица 1 - Исходные данные Душевой доход (X) (ден. ед) Расход на потребление товара А (Y) (ден. ед) X² X*Y Y² 200,00 114,00 40 000 ...
... взяты за 2003 год. Данные взяты из статистического сборника Регионы России Социально-экономические показатели. 2003. Федеральная служба государственной статистики Построение модели множественной регрессии Расчет параметров Рассчитаем необходимые параметры: Признак Ср. знач. СКО Характеристики тесноты связи βi bi Коэф-ты частной корр. F-критерий фактический ...
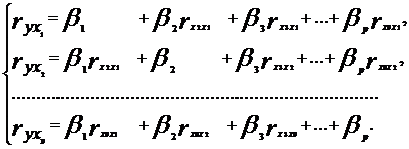
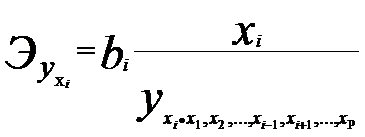
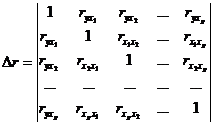
0 комментариев