Навигация
Для обнаружения тенденции в данном ВР воспользуемся критерием "восходящих и нисходящих" серий
2. Для обнаружения тенденции в данном ВР воспользуемся критерием "восходящих и нисходящих" серий.
Критерий "восходящих и нисходящих" серий
1) Для исследуемого ВР определяется последовательность знаков, исходя из условий: (+), если ![]() , (-), если
, (-), если ![]() .
.
При этом, если последующее наблюдение равно предыдущему, то учитывается только одно наблюдение.
2) Подсчитывается число серий ![]() . Под серией понимается последовательность подряд расположенных плюсов или минусов, причем один плюс или один минус считается серией.
. Под серией понимается последовательность подряд расположенных плюсов или минусов, причем один плюс или один минус считается серией.
3) Определяется протяженность самой длинной серии ![]() .
.
4) Значение ![]() находят из следующей таблицы:
находят из следующей таблицы:
Таблица №25
| Длина ряда, |
|
|
|
| Значение | 5 | 6 | 7 |
5) Если нарушается хотя бы одно из следующих неравенств, то гипотеза об отсутствии тренда отвергается с доверительной вероятностью 0,95
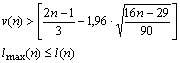
Определим последовательность знаков:
Таблица №19
| t | Выпуск продукции, yt млн.долл. |
|
| 1 | 23 298 | |
| 2 | 26 570 | + |
| 3 | 23 080 | - |
| 4 | 29 800 | + |
| 5 | 28 440 | - |
| 6 | 29 658 | + |
| 7 | 39 573 | + |
| 8 | 38 435 | - |
| 9 | 39 002 | + |
| 10 | 39 020 | + |
| 11 | 40 012 | + |
| 12 | 41 005 | + |
| 13 | 39 080 | - |
| 14 | 42 680 | + |
Определим число серий ![]() :
: ![]() . Определим протяженность самой длинной серии
. Определим протяженность самой длинной серии ![]() :
: ![]() .
. ![]() , так как
, так как ![]() . Проверим выполнение неравенств:
. Проверим выполнение неравенств:
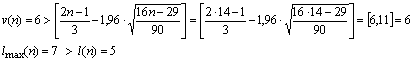
Вывод: второе неравенство не выполняются, следовательно, тренд (тенденция) в динамике выпуска продукции имеется на уровне значимости 0,05. Среднее значение ![]() . Среднее значение
. Среднее значение ![]() . Вычислим коэффициенты автокорреляции первого и второго порядков, то есть для лагов
. Вычислим коэффициенты автокорреляции первого и второго порядков, то есть для лагов ![]() . Подготовим данные для вычисления коэффициентов автокорреляции первого и второго порядков. Дополним таблицу данных двумя столбцами
. Подготовим данные для вычисления коэффициентов автокорреляции первого и второго порядков. Дополним таблицу данных двумя столбцами ![]() .
.
Таблица №20
| t | Yt | Yt-1 | Yt-2 |
| 1 | 23 298 | ||
| 2 | 26 570 | 23 298 | |
| 3 | 23 080 | 26 570 | 23 298 |
| 4 | 29 800 | 23 080 | 26 570 |
| 5 | 28 440 | 29 800 | 23 080 |
| 6 | 29 658 | 28 440 | 29 800 |
| 7 | 39 573 | 29 658 | 28 440 |
| 8 | 38 435 | 39 573 | 29 658 |
| 9 | 39 002 | 38 435 | 39 573 |
| 10 | 39 020 | 39 002 | 38 435 |
| 11 | 40 012 | 39 020 | 39 002 |
| 12 | 41 005 | 40 012 | 39 020 |
| 13 | 39 080 | 41 005 | 40 012 |
| 14 | 42 680 | 39 080 | 41 005 |
![]() .
.
![]() .
.
Вывод:
1) высокое значение коэффициента автокорреляции первого порядка ![]() свидетельствует об очень тесной зависимости между выпуском продукции текущего и непосредственно предшествующего годов, и, следовательно, о наличии в исследуемом временном ряде сильной линейной тенденции;
свидетельствует об очень тесной зависимости между выпуском продукции текущего и непосредственно предшествующего годов, и, следовательно, о наличии в исследуемом временном ряде сильной линейной тенденции;
2) исследуемый ряд содержит только тенденцию, так как наиболее высоким оказался коэффициент автокорреляции первого порядка (0,85>0,83).
Скользящие средние найдем по формуле: ![]() , здесь
, здесь ![]() . При
. При ![]()
Вычисляем:
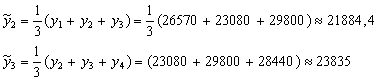
и так далее.
Результаты вычислений занесем в таблицу и построим графики исходного![]() и сглаженного
и сглаженного ![]() рядов в одной координатной плоскости.
рядов в одной координатной плоскости.
Таблица №21
| t | yi | yt |
| 1 | 23 298 | |
| 2 | 26 570 | 24 315,76 |
| 3 | 23 080 | 26 483,07 |
| 4 | 29 800 | 27 106,40 |
| 5 | 28 440 | 29 299,04 |
| 6 | 29 658 | 32 556,67 |
| 7 | 39 573 | 35 888,31 |
| 8 | 38 435 | 39 002,94 |
| 9 | 39 002 | 38 818,61 |
| 10 | 39 020 | 39 344,27 |
| 11 | 40 012 | 40 011,93 |
| 12 | 41 005 | 40 031,93 |
| 13 | 39 080 | 40 921,26 |
| 14 | 42 680 |
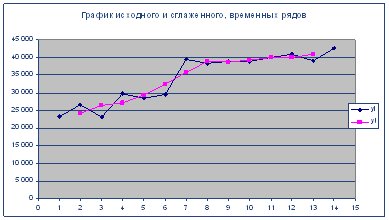
Таблица № Параметры (коэффициенты) уравнения тренда.
Таблица №22
| Коэффициенты | |
| Y-пересечение | 22686,54945 |
| t | 1543,250549 |
Анализ данных таблицы Дисперсионного анализа показывает, что получено статистически значимое уравнение, так как наблюдаемое значение ![]() , равное 52,785, превышает его табличное значение
, равное 52,785, превышает его табличное значение ![]() ,
, ![]() . Вывод: Таким образом, параметры уравнения тренда статистически значимы на уровне
. Вывод: Таким образом, параметры уравнения тренда статистически значимы на уровне ![]() : уравнение тренда можно использовать для прогноза.
: уравнение тренда можно использовать для прогноза.
Сделаем точечный и интервальный (с надежностью 0,95) прогнозы среднего и индивидуального значений прогнозов на 2003 год.
Определим точечный прогноз
![]()
![]()
Вычислим интервальный прогноз:
Так как тренд является прямой, то доверительный интервал можно представить в виде: ![]()
![]() .
.
Здесь стандартная ошибка предсказания по линии тренда ![]() вычисляется по формуле:
вычисляется по формуле:
 ,
,
здесь величина ![]() является стандартной ошибкой регрессии, и ее значение находится в таблице Регрессионная статистика
является стандартной ошибкой регрессии, и ее значение находится в таблице Регрессионная статистика
Таблица №23
| Стандартная ошибка | 1637,180026 |
![]() кратность ошибки (надежность) находят по таблице значений критерия Стьюдента;
кратность ошибки (надежность) находят по таблице значений критерия Стьюдента; ![]() уровень значимости;
уровень значимости; ![]() число степеней свободы.
число степеней свободы.
Итак, по условию задачи имеем: ![]()
Для вычисления стандартной ошибки предсказания по линии тренда ![]() необходимо вычислить
необходимо вычислить ![]() и сумму
и сумму ![]() .
.
Таблица № 24
| t | yt | (t1-tcr) ^2 |
| 1 | 23 298 | 42,25 |
| 2 | 26 570 | 30,25 |
| 3 | 23 080 | 20,25 |
| 4 | 29 800 | 12,25 |
| 5 | 28 440 | 6,25 |
| 6 | 29 658 | 2,25 |
| 7 | 39 573 | 0,25 |
| 8 | 38 435 | 0,25 |
| 9 | 39 002 | 2,25 |
| 10 | 39 020 | 6,25 |
| 11 | 40 012 | 12,25 |
| 12 | 41 005 | 20,25 |
| 13 | 39 080 | 30,25 |
| 14 | 42 680 | 42,25 |
| 7,5 | Сумма | 227,5 |
Вычисляем 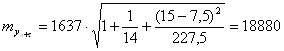 (млн. долл.)
(млн. долл.)
По таблице значений критерия Стьюдента найдем ![]()
Максимальная ошибка прогноза будет равна:
![]() (млн. долл.).
(млн. долл.).
Нижняя граница прогноза имеет значение ![]() (млн. долл.)
(млн. долл.)
Верхняя граница прогноза имеет значение ![]() (млн. долл.)
(млн. долл.)
Вывод:
1) значение выпуска продукции Финляндии в 2003 составит 20111,2 млн. долл.
2) с надежностью 0,95 данное значение будет находиться в интервале ![]()
Похожие работы
... и детерминации и F-критериев Фишера наибольшие. 3. Множественная регрессия Цель работы – овладеть методикой построения линейных моделей множественной регрессии, оценки их существенности и значимости, расчетом показателей множественной регрессии и корреляции. Постановка задачи. По данным изучаемых регионов (таблица 1) изучить зависимость общего коэффициента рождаемости () от уровня бедности ...
... и все коэффициенты корреляции равны 1, то определитель такой матрицы равен 0: . Чем ближе к 0 определитель матрицы межфакторной корреляции, тем сильнее мультиколлинеарность факторов и ненадежнее результаты множественной регрессии. И наоборот, чем ближе к 1 определитель матрицы межфакторной корреляции, тем меньше мультиколлинеарность факторов. Проверка мультиколлинеарности факторов может быть ...
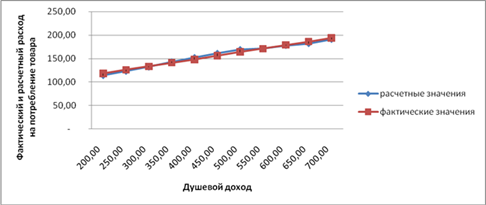
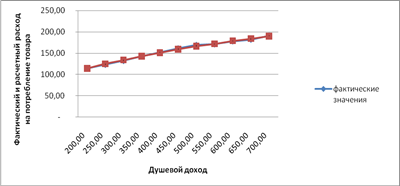
трех исследованных моделей. Отбор факторов и показателей для построения функции потребления Исходные данные, характеризующие изменение душевого дохода (Х) и расхода на потребление товара А (Y) приведены в таблице 1. Таблица 1 - Исходные данные Душевой доход (X) (ден. ед) Расход на потребление товара А (Y) (ден. ед) X² X*Y Y² 200,00 114,00 40 000 ...
... взяты за 2003 год. Данные взяты из статистического сборника Регионы России Социально-экономические показатели. 2003. Федеральная служба государственной статистики Построение модели множественной регрессии Расчет параметров Рассчитаем необходимые параметры: Признак Ср. знач. СКО Характеристики тесноты связи βi bi Коэф-ты частной корр. F-критерий фактический ...
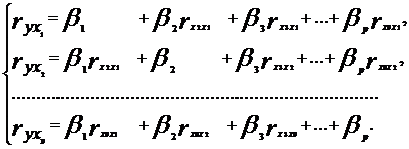
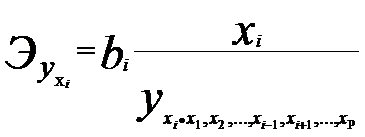
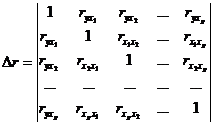
0 комментариев