Навигация
Классические примеры решения некоторых типовых задач
3. Классические примеры решения некоторых типовых задач
Пример 1
Чему равен момент инерции ![]() цилиндра с диаметром основания
цилиндра с диаметром основания ![]() d и высотой Н относительно оси
d и высотой Н относительно оси ![]() совпадающей с его образующей? Плотность материала цилиндра
совпадающей с его образующей? Плотность материала цилиндра ![]() .
.
Дано:
d;
Н;
![]() .
.
![]()
![]() ?
?
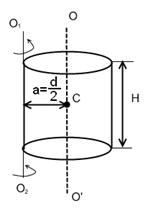
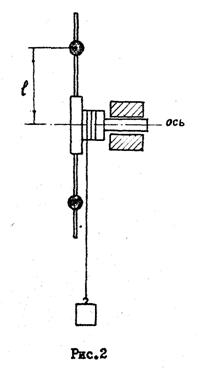
Рис. 2
Решение: Согласно теоремы Штейнера момент инерции цилиндра ![]() относительно оси
относительно оси ![]() равен сумме его момента инерции
равен сумме его момента инерции ![]() относительно оси симметрии
относительно оси симметрии ![]() , проходящей через центр цилиндра С, и произведения массы цилиндра
, проходящей через центр цилиндра С, и произведения массы цилиндра ![]() на квадрат расстояния
на квадрат расстояния ![]() между осями
между осями ![]() и
и ![]() :
:
![]() .(1)
.(1)
Момент инерции цилиндра ![]() относительно оси
относительно оси ![]() определяется формулой
определяется формулой ![]()
![]() , где
, где ![]() , поэтому
, поэтому
![]()
![]() .(2)
.(2)
Массу цилиндра выразим через его плотность ![]() и объем
и объем ![]() :
:
![]() , где
, где ![]() , поэтому
, поэтому ![]() ; площадь основания цилиндра
; площадь основания цилиндра ![]() и, следовательно,
и, следовательно,
![]() .(3)
.(3)
Расстояние между осями ![]() и
и ![]()
![]() . (4)
. (4)
Подставив (2), (3) и (4) в (1), получаем
![]()
![]() +
+![]()
Пример 2
Два маленьких шарика массой ![]() 10 г каждый скреплены тонким невесомым стержнем длиной
10 г каждый скреплены тонким невесомым стержнем длиной ![]() 20 см. Определить момент инерции
20 см. Определить момент инерции ![]() системы, относительно оси, перпендикулярной стержню и проходящей через центр масс.
системы, относительно оси, перпендикулярной стержню и проходящей через центр масс.
Дано:
![]() 10 г
10 г![]() 10-2 кг;
10-2 кг;
![]() 20 см
20 см![]() 0,2 м.
0,2 м.
![]()
![]() ?
?
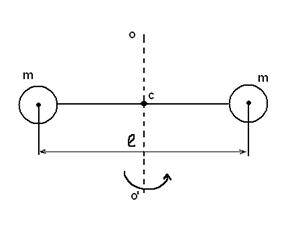
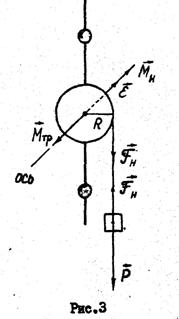
Рис. 3
Решение: Общий момент инерции, проходящий через центр масс системы (точка С) равен сумме моментов инерции двух материальных точек массой ![]() каждая и вращающихся вокруг оси
каждая и вращающихся вокруг оси ![]() на расстоянии
на расстоянии ![]() .
.
![]() 2.10-4 кг
2.10-4 кг![]() м2.
м2.
Пример 3
Найти момент инерции ![]() плоской однородной прямоугольной пластины массой
плоской однородной прямоугольной пластины массой ![]() 800 г относительно оси, совпадающей с одной из её сторон, если длина другой стороны равна а
800 г относительно оси, совпадающей с одной из её сторон, если длина другой стороны равна а![]() 30 см.
30 см.
Дано:
![]() 800 г
800 г![]() 0,8 кг;
0,8 кг;
а![]() 30 см
30 см![]() 0,3 м.
0,3 м.
![]() ?
?
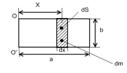
Рис. 4
Решение: Найдем момент инерции пластины относительно оси ![]() . Для этого разобьем пластину на бесконечно малые участки массой
. Для этого разобьем пластину на бесконечно малые участки массой ![]() (один из них выделен на рис. 4).
(один из них выделен на рис. 4).
![]() ,(1)
,(1)
где ![]() - поверхностная плотность пластины;
- поверхностная плотность пластины;
![]() - площадь пластины.
- площадь пластины.
Так как участок массой ![]() можно считать материальной точкой, то момент инерции этого участка относительно оси
можно считать материальной точкой, то момент инерции этого участка относительно оси ![]()
![]() .(2)
.(2)
После подстановки выражения (1) в (2) получаем
![]() .(3)
.(3)
Складывая моменты инерции всех участков, проинтегрируем полученное выражение в пределах от 0 до а:
![]() .(4)
.(4)
Подставив численные значения, найдем
![]() 2,4
2,4![]() 10-2 кг
10-2 кг![]() м2.
м2.
Пример 4
Обруч массой ![]() 1 кг и радиусом
1 кг и радиусом ![]() 0,2 м вращается равномерно с частотой
0,2 м вращается равномерно с частотой ![]() 3 с-1 относительно оси
3 с-1 относительно оси ![]() , проходящей через середину его радиуса перпендикулярно плоскости обруча. Определить момент импульса обруча
, проходящей через середину его радиуса перпендикулярно плоскости обруча. Определить момент импульса обруча ![]() .
.
Дано:
![]() 1 кг;
1 кг;
![]() 0,2 м;
0,2 м;
![]() 3 с-1.
3 с-1.
![]() ?
?
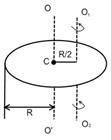
Рис. 5
Решение: Момент импульса твердого тела равен произведению момента инерции этого тела ![]() и его угловой скорости
и его угловой скорости ![]() :
:
![]() .(1)
.(1)
Момент инерции обруча относительно оси ![]() по теореме Штейнера равен сумме момента инерции этого обруча
по теореме Штейнера равен сумме момента инерции этого обруча ![]() относительно оси
относительно оси ![]() , проходящей через его центр С, и произведения массы обруча
, проходящей через его центр С, и произведения массы обруча ![]() на квадрат расстояния
на квадрат расстояния ![]() между осями
между осями ![]() и
и ![]() , которое, как следует из рисунка, равно
, которое, как следует из рисунка, равно
![]() :
:
![]() ,(2)
,(2)
где ![]() . (3)
. (3)
Угловая скорость ![]() обруча связана с его частотой вращения
обруча связана с его частотой вращения ![]() соотношением
соотношением
![]() .(4)
.(4)
Подставив выражение (2), (3) и (4) в (1), получаем
![]()
![]() 0,94 кг
0,94 кг![]() м2
м2![]() с-1.
с-1.
Пример 5
Вал в виде сплошного цилиндра массой ![]() 12 кг насажен на горизонтальную ось. На цилиндр намотан шнур, к свободному концу которого подвешена гиря массой
12 кг насажен на горизонтальную ось. На цилиндр намотан шнур, к свободному концу которого подвешена гиря массой ![]() 4 кг. С каким ускорением а будет опускаться гиря, если её предоставить самой себе?
4 кг. С каким ускорением а будет опускаться гиря, если её предоставить самой себе?
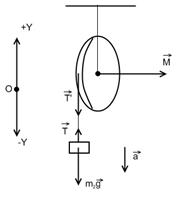
Рис. 6
Дано:
![]() 12 кг;
12 кг;
![]() 4 кг;
4 кг;
![]() 10 м/с2.
10 м/с2.
____________
а ![]() ?
?
Решение: Линейное ускорение а гири равно тангенциальному ускорению точек вала, лежащих на его цилиндрической поверхности, и связано с угловым ускорением ![]() вала соотношением
вала соотношением
![]() ,(1)
,(1)
где ![]() радиус вала. Угловое ускорение вала выражается основным уравнением динамики вращающегося тела:
радиус вала. Угловое ускорение вала выражается основным уравнением динамики вращающегося тела:
![]() ,(2)
,(2)
где ![]() вращающий момент, действующий на вал;
вращающий момент, действующий на вал; ![]() - момент инерций вала.
- момент инерций вала.
Рассмотрим вал как однородный цилиндр. Тогда его момент инерции относительно геометрической оси равен
![]() .(3)
.(3)
Вращающий момент М, действующий на вал, равен произведению силы натяжения нити Т шнура на радиус вала:
![]() .(4)
.(4)
(Учитывая, что шнур невесомый и нерастяжимый, ![]() ).
).
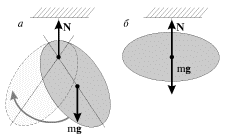
Силу натяжения шнура найдем из следующих соображений. На гирю действуют две силы: силы тяжести ![]() , направленная вниз, и сила натяжения
, направленная вниз, и сила натяжения ![]() шнура, направленная вверх; равнодействующая этих сил вызывает равноускоренное движение гири. По второму закону Ньютона
шнура, направленная вверх; равнодействующая этих сил вызывает равноускоренное движение гири. По второму закону Ньютона ![]() , откуда
, откуда
![]() .(5)
.(5)
Таким образом, вращающий момент равен
![]() .(6)
.(6)
Подставив в (2) выражения (3) и (6), получаем
![]() .(7)
.(7)
Ускорение гири найдем из (1) после подстановки туда выражения (7) ![]() , откуда
, откуда
![]() 4 м/с2.
4 м/с2.
Пример 6
Однородный диск радиусом ![]() 0,2 м и массой
0,2 м и массой ![]() 5 кг вращается вокруг оси, проходящей через его центр перпендикулярно плоскости диска. Зависимость угла поворота диска от времени даётся уравнением
5 кг вращается вокруг оси, проходящей через его центр перпендикулярно плоскости диска. Зависимость угла поворота диска от времени даётся уравнением ![]() где С=2 рад/с2. Вращению диска противодействует тормозящий момент сил трения
где С=2 рад/с2. Вращению диска противодействует тормозящий момент сил трения ![]() 1 Н
1 Н![]() м. Определить величину касательной силы
м. Определить величину касательной силы ![]() , приложенной к ободу диска.
, приложенной к ободу диска.
Дано:
![]() 0,2 м;
0,2 м;
![]() 5 кг;
5 кг;
![]() ;
;
С=2 рад/с2;
![]() 1 Н
1 Н![]() м.
м.
![]() ?
?
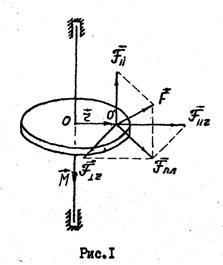
Рис. 7
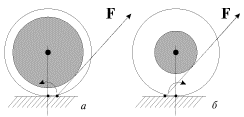
Решение: Касательная сила ![]() , приложенная к ободу диска, создает вращающий момент сил
, приложенная к ободу диска, создает вращающий момент сил ![]() , который по определению момента сил равен произведению величины этой силы
, который по определению момента сил равен произведению величины этой силы ![]() и её плеча; плечом силы
и её плеча; плечом силы ![]() в нашем случае является радиус диска, поэтому
в нашем случае является радиус диска, поэтому
![]() .(1)
.(1)
Вращающему моменту сил ![]() противодействует момент сил трения
противодействует момент сил трения ![]() .
.
Согласно основному уравнению динамики вращательного движения произведение момента инерции диска ![]() и его углового ускорения
и его углового ускорения ![]() равно векторной сумме моментов сил, приложенных к диску относительно центра вращения тч. О.
равно векторной сумме моментов сил, приложенных к диску относительно центра вращения тч. О.
![]() (2)
(2)
Поскольку векторы моментов сил ![]() и
и ![]() антинаправлены (в чём можно убедиться, используя правило правого винта), то в проекциях на ось ОХ этот закон примет вид
антинаправлены (в чём можно убедиться, используя правило правого винта), то в проекциях на ось ОХ этот закон примет вид
![]() .(3)
.(3)
Момент инерции диска относительно оси вращения определяется по формуле
![]() .(4)
.(4)
Угловое ускорение диска найдем как вторую производную угла поворота диска по времени:
![]() ,
, ![]() .(5)
.(5)
Решая совместно (1) – (5), получаем
![]() .(6)
.(6)
После подстановки в (6) численных значений
![]() 7 Н.
7 Н.
Пример 7
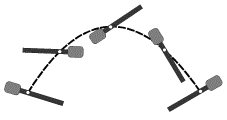
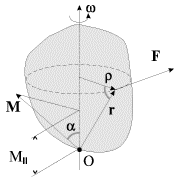
Вследствие действия приливов продолжительность суток на Земле увеличивается за время ![]() 100 лет на
100 лет на ![]() 10-3 с. Определите приливную силу трения. Землю считать однородным шаром массой
10-3 с. Определите приливную силу трения. Землю считать однородным шаром массой ![]() 6
6![]() 1024 кг и радиусом
1024 кг и радиусом ![]() 6,4
6,4![]() 106м.
106м.
Дано:
Похожие работы
... ВПО «ЧЕРЕПОВЕЦКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ» Факультет общих математических и естественнонаучных дисциплин Кафедра общей физики ЛАБОРАТОРНАЯ РАБОТА №23 Проверка основного закона динамики вращательного движения твердого тела относительно неподвижной оси выполнил: студент гр. 5СКб-11 Череповец, 2009/10 уч. Год проверил: ассис. Герасимов Р.А. Введение ...
... , нужно посредством правил подсчета значащих цифр округлить результат математических вычислений так, чтобы точность их соответствовала точности данных, полученных от измерения. ИЗУЧЕНИЕ КИНЕМАТИКИ И ДИНАМИКИ ПОСТУПАТЕЛЬНОГО ДВИЖЕНИЯ НА МАШИНЕ АТВУДА Цель работы Экспериментальная проверка основных уравнений и законов поступательного движения тела на специально сконструированной для этого ...
... (3.2) Здесь L- момент импульса твердого тела относительно некоторой точки, - суммарный момент внешних сил относительно той же самой точки. К уравнениям (3.1) и (3.2), являющимся уравнениями динамики твердого тела, необходимо дать следующие комментарии: 1. Внутренние силы, как и в случае произвольной системы материальных точек, не- влияют на движение центра масс и не могут изменить ...
... в 2 раза. 180. Найти относительную скорость движения двух частиц, движущихся навстречу друг другу со скоростями u1 = 0,6×c и u2 = 0,9×c. II. ОСНОВЫ МОЛЕКУЛЯРНОЙ ФИЗИКИ И ТЕРМОДИНАМИКИ Молекулярная физика и термодинамика – разделы физики, в которых изучаются макроскопические процессы в телах, связанные с огромным числом содержащихся в них атомов и молекул (макроскопические системы ...



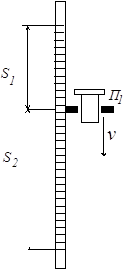



0 комментариев