Навигация
Математические методы и модели в экономике
ФЕДЕРАЛЬНОЕ АГЕНТСТВО ПО ОБРАЗОВАНИЮ
ГОСУДАРСТВЕННОЕ ОБРАЗОВАТЕЛЬНОЕ УЧРЕЖДЕНИЕ ВЫСШЕГО ПРОФЕССИОНАЛЬНОГО ОБРАЗОВАНИЯ
КАМСКАЯ ГОСУДАРСТВЕННАЯ ИНЖЕНЕРНО-ЭКОНОМИЧЕСКАЯ АКАДЕМИЯ
КАФЕДРА ЭОУП
КОНТРОЛЬНАЯ РАБОТА
по дисциплине "Математические методы и модели в экономике"
Выполнил: студент гр. 4381-С
Кустовский Р.Г.
Проверил: доцент
Коврижных О.Е.
г. Набережные Челны
2010
ЗАДАНИЕ 1
Построить одноиндексную математическую модель задачи линейного программирования. В модели надо указать единицы измерения всех переменных, целевой функции и каждого ограничения
Цех мебельного комбината выпускает трельяжи, трюмо и тумбочки под телевизоры. Норма расхода материала в расчете на одно изделие, плановая себестоимость, оптовая цена предприятия, плановый ассортимент и трудоемкость единицы продукции приведены в таблице. При этом, запас древесно-стружечных плит, досок еловых и березовых 92, 33 и 17 куб.м. соответственно. Плановый фонд рабочего времени 19100 человеко-часов.
Исходя из необходимости выполнения плана по ассортименту и возможности его перевыполнения по отдельным (и даже всем) показателям, постройте модель, на основе которой можно найти план производства, максимизирующий прибыль.
| Показатели | Изделия | ||
| трельяж | трюмо | тумбочка | |
| Норма расхода материала, куб.м.: | |||
| древесно-стружечные плиты | 0,042 | 0,037 | 0,028 |
| доски еловые | 0,024 | 0,018 | 0,081 |
| доски березовые | 0,007 | 0,008 | 0,005 |
| Трудоемкость, чел.-ч. | 7,5 | 10,2 | 6,7 |
| Плановая себестоимость, ден.ед. | 98,81 | 65,78 | 39,42 |
| Оптовая цена предприятия, ден.ед. | 97,10 | 68,20 | 31,70 |
| Плановый ассортимент, шт. | 450 | 1200 | 290 |
Решение:
В условии задачи сформулирована цель получение максимальной прибыли при необходимости выполнения плана по ассортименту и возможности его перевыполнения. Поэтому, искомыми величинами, а значит, и переменными задачи являются количество произведенной продукции:
Х1 - количество изготовленных трельяжей.
Х2 - количество изготовленных трюмо.
Х3 - количество изготовленных тумбочек.
Поэтому целевой функцией будет математическое выражение, в которой суммируется прибыль от изготовления каждой продукции. Прибыль является разность между себестоимостью и оптовой ценой продукции.
L = (97,10 – 98,81) *Х1 + (68,2 – 65,78)* Х2 +(31,7 – 39,42)* Х3 =
= –1,71 * Х1+ 2,42 * Х2 – 7,72 * Х3 àmax
Условием является то, что сумма расхода материалов не должно быть больше имеющихся материалов, а так же обязательное условие - выполнение плана. Таким образом, математическая модель задачи будет иметь вид:
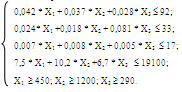
ЗАДАНИЕ 2
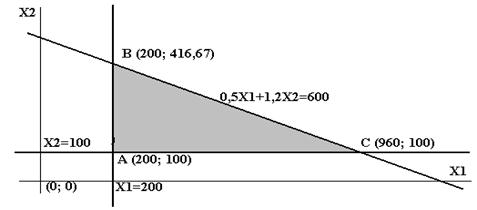
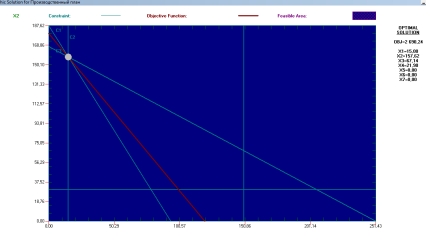
Решить одноиндексную задачу линейного программирования графическим методом.

Построим следующие прямые:
х1 + х2 = 2 (1)
-х1 + х2 = 4 (2)
х1 + 2х2 = 8 (3)
х1 = 6 (4)
Для этого вычислим координаты прямых:

Заштрихуем полуплоскости, определяемые и разрешаемые каждым из ограничений неравенств. Определим область допустимых решений , многоугольник АВCDEF.
Построим целевую функцию по уравнению

Нижняя точка пересечения целевой функции и многоугольника – это точка минимума целевой функции.
Найдем координаты точки D ( 2; 0 ).
Минимальное значение целевой функции
L(Х) = L(D) = 1*2 + 3*0 = 2
ЗАДАНИЕ 3
Задача сетевого планирования
По данным варианта необходимо:
1) построить сетевую модель, рассчитать временные параметры событий (на рисунке) и работ (в таблице);
2) определить критические пути модели;
3) оптимизировать сетевую модель по критерию "минимум исполнителей" (указать какие работы надо сдвигать и на сколько дней, внесенные изменения показать на графиках привязки и загрузки пунктирной линией).
| Название работы | Нормальная длительность | Количество исполнителей | Вариант 2 (N=11 человек) 1. D - исходная работа проекта; 2. Работа E следует за D; 3. Работы A, G и C следуют за E; 4. Работа B следует за A; 5. Работа H следует за G; 6. Работа F следует за C; Работа I начинается после завершения B, H, и F |
| A | 3 | 5 | |
| B | 4 | 7 | |
| C | 1 | 1 | |
| D | 4 | 3 | |
| E | 5 | 2 | |
| F | 7 | 3 | |
| G | 6 | 6 | |
| H | 5 | 1 | |
| I | 8 | 5 |
Похожие работы
... с помощью двухэтапного метода, совпадает с решением, полученным в среде MS Excel с помощью программной надстройки «Поиск решения». 7. ПРИМЕРЫ ПОСТАНОВОК, ФОРМАЛИЗАЦИИ И РЕШЕНИЯ ПЕРСПЕКТИВНЫХ ОПТИМИЗАЦИОННЫХ УПРАВЛЕНЧЕСКИХ ЗАДАЧ Одним из методов решения задач линейного программирования является графический метод, применяемый для решения тех задач, в которых имеются только две переменные, ...
... или тактические управленческие решения. Исторически сложились две группы способов и приемов: традиционные и математические. Рассмотрим подробнее применение математических методов в экономическом анализе. Математические методы в экономическом анализе Использование математических методов в сфере управления - важнейшее направление совершенствования систем управления. Математические методы ускоряют ...
... Ю.Н. Математические методы в экономике: Учебник.2-е изд. – М.: МГУ им. М.В. Ломоносова, Издательство «Дело и Сервис», 1999. – 368 с. 7. Монахов А.В. Математические методы анализа экономики. – Спб: Питер, 2002. – 176 с. 8. Экономико-математические методы и прикладные модели: Учеб. пособие для вузов /В.В. Федосеев, А.Н. Гармаш, Д.М. Дайитбегов и др., Под ред. В.В. Федосеева. – М.: ЮНИТИ, 1999. ...
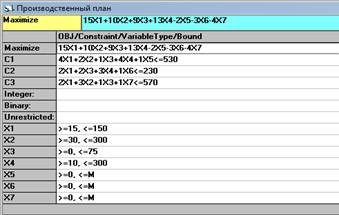
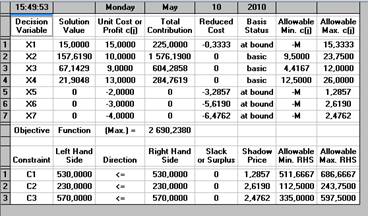
... : Ресурсы А В С D Наличие Ресурс R1 4 2 1 4 530 Ресурс R2 2 - 2 3 230 Ресурс R3 2 3 1 - 570 Прибыль 15 10 9 13 Нижн. гр. 15 30 0 10 Верхн. гр. 150 300 75 300 Построим математическую модель задачи, обозначив количество выпускаемых изделий через х1, х2, х3, х4, а целевую функцию (валовую маржинальную прибыль) — через F: F(х) = 15х1 + 10х2 + 9х3 + ...
0 комментариев