Навигация
Определим критические пути модели
2. Определим критические пути модели
Критический путь – 1,2,3,6,7,8 = 28 суток - максимальный по продолжительности полный путь.
3. Оптимизируем сетевую модель по критерию "минимум исполнителей" (укажем какие работы надо сдвигать и на сколько дней, внесенные изменения показать на графиках привязки и загрузки пунктирной линией).
Построим график привязки для следующих исходных данных.
| Название работы |
|
| Количество исполнителей |
| D | 1-2 | 4 | 3 |
| E | 2-3 | 5 | 2 |
| A | 3-5 | 3 | 5 |
| G | 3-6 | 6 | 6 |
| C | 3-4 | 1 | 1 |
| B | 5-7 | 4 | 7 |
| H | 6-7 | 5 | 1 |
| F | 4-7 | 7 | 3 |
| I | 7-8 | 8 | 5 |
При оптимизации использования ресурса рабочей силы сетевые работы чаще всего стремятся организовать таким образом, чтобы:
· количество одновременно занятых исполнителей было минимальным;
· выровнять потребность в людских ресурсах на протяжении срока выполнения проекта.
Проведенная оптимизация была основана на использовании свободных и полных резервов работ.
Для этого необходимо чуть дальше сдвинуть указанные работы, а именно: работу (3,5) сдвинуть на 1 дней, работу (5,7) - на 3 дня, и работу (4,7) на 3 дня.
В результате оптимизации количество одновременно занятых исполнителей снизили с 16 человек до 11.
ЗАДАНИЕ 4
Решить задачу управления запасами.
Завод радиоэлектронной аппаратуры производит 860 радиоприемников в сутки. Микросхемы для радиоприемников (по 1 шт. на приемник) производятся на этом же заводе с интенсивностью 3420 тыс. шт. в сутки. Затраты на подготовку производства партии микросхем составляют 81 руб. (числа в задаче условные), себестоимость производства 1 тыс. шт. микросхем равна 25 руб. Хранение микросхем на складе обходится заводу в 1,5 руб. за каждую тысячу в сутки. У завода появилась возможность закупать микросхемы в другом месте по цене 25 руб. за 1 тыс. шт. Стоимость доставки равна 32 руб.
Выясните, стоит ли заводу закупать микросхемы вместо того, чтобы их производить. Для более выгодного режима работы завода (производство или закупка) определите периодичность подачи заказа, и затраты на управление запасами в месяц (22 рабочих дня).
1. Для моделирования процессов производства продукции применим модель планирования экономичного размера партии.
Размер партии микросхем, производимых на заводе:
Q* = Ö (2К1*n*l)/(S(l-n)
Q* = Ö (2*81*0,86*3420) /(1,5*(3420 – 0,86) = 9,639 тыс. шт.
Частота запуска микросхем в производство:
t1=(Q*/n)*q
t1= (9,639/0,86)*22 = 246,6 часов ~ 4,1 ~ 4 рабочих дней
Общие затраты на управление запасами:
L1 = К1*(n/Q*) + S*( Q*(l - n))/(2l) + Сin
L1 = 81*(0,860/9,639) + 1,5* (9,639*(3420 – 0,86))/(2*3420) + 25*0,86 = 36 руб/сут.
L1 = 36 *22 = 792 руб/мес.
2. Моделирование процесса закупки произведем с помощью модели Уилсона.
Размер партии заказа:
Qw = Ö2*К2n/S
Qw= Ö2*32*0,86/1,5= 6,057 тыс. шт
Подача каждого нового заказа должна производиться через:
t2 = (Qw/n)*q
t2 = (6,057/0,86)*22 = 154,946 часов ~ 5,16 ~ 5 раб. дней
Затраты на управление запасами:
L2 = К2*(n/Q) + S*(Q/2) + С2n
L2 = 32*(0,86/6,057) + 1,5*(6,057/2) + 25*0,86 = 30,6 руб./сут
L2 = 30,6 *22 = 672,9 руб./мес.
Ответ: таким образом, можно сделать вывод, что заводу выгодно покупать микросхемы у внешнего источника, чем производить их самим, расходы в этом случае меньше.
Похожие работы
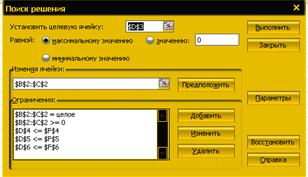
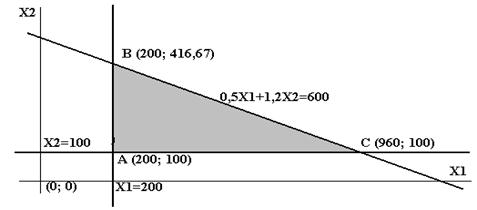
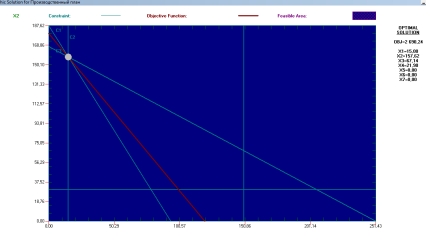
... с помощью двухэтапного метода, совпадает с решением, полученным в среде MS Excel с помощью программной надстройки «Поиск решения». 7. ПРИМЕРЫ ПОСТАНОВОК, ФОРМАЛИЗАЦИИ И РЕШЕНИЯ ПЕРСПЕКТИВНЫХ ОПТИМИЗАЦИОННЫХ УПРАВЛЕНЧЕСКИХ ЗАДАЧ Одним из методов решения задач линейного программирования является графический метод, применяемый для решения тех задач, в которых имеются только две переменные, ...
... или тактические управленческие решения. Исторически сложились две группы способов и приемов: традиционные и математические. Рассмотрим подробнее применение математических методов в экономическом анализе. Математические методы в экономическом анализе Использование математических методов в сфере управления - важнейшее направление совершенствования систем управления. Математические методы ускоряют ...
... Ю.Н. Математические методы в экономике: Учебник.2-е изд. – М.: МГУ им. М.В. Ломоносова, Издательство «Дело и Сервис», 1999. – 368 с. 7. Монахов А.В. Математические методы анализа экономики. – Спб: Питер, 2002. – 176 с. 8. Экономико-математические методы и прикладные модели: Учеб. пособие для вузов /В.В. Федосеев, А.Н. Гармаш, Д.М. Дайитбегов и др., Под ред. В.В. Федосеева. – М.: ЮНИТИ, 1999. ...
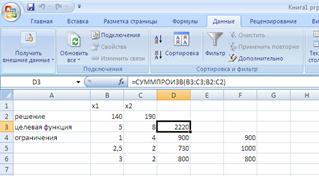
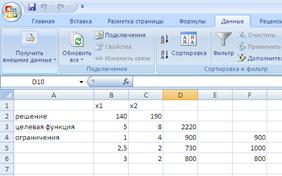
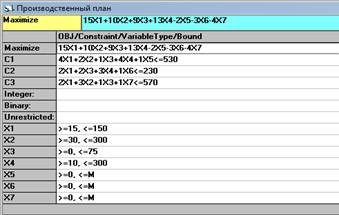
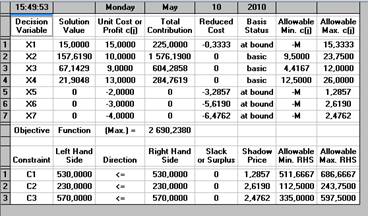
... : Ресурсы А В С D Наличие Ресурс R1 4 2 1 4 530 Ресурс R2 2 - 2 3 230 Ресурс R3 2 3 1 - 570 Прибыль 15 10 9 13 Нижн. гр. 15 30 0 10 Верхн. гр. 150 300 75 300 Построим математическую модель задачи, обозначив количество выпускаемых изделий через х1, х2, х3, х4, а целевую функцию (валовую маржинальную прибыль) — через F: F(х) = 15х1 + 10х2 + 9х3 + ...
0 комментариев