Навигация
Перетин поверхонь геометричних тіл прямою та площиною
3. Перетин поверхонь геометричних тіл прямою та площиною
Перетин багатогранників площиною та прямою лінією
Ми визначили що багатогранник – це геометричне тіло, обмежене плоскими гранями. Грані, перетинаючись, утворюють сітку багатогранника, складену з ребер і вершин. Зображення багатогранника на кресленні зводиться до побудови проекцій його сітки.
Площина перетинає багатогранник по багатокутнику, вершини якого є точками перетину січної площини з ребрами, а сторони – лініями перетину січної площини з гранями. Таким чином, побудова багатокутника перерізу зводиться до розв’язування відомих позиційних задач: побудова точки перетину прямої з площиною або лінії перетину двох площин. Відповідно розрізняють два способи побудови: спосіб ребер і спосіб граней.
Використовуючи спосіб ребер, визначають вершини багатокутника перерізу як точки перетину ребер багатогранника з січною площиною. Так, точка А є точкою перетину ребра піраміди 1S з площиною Г, В-ребра 2S і С – ребра 3S. Трикутник АВС – шуканий переріз піраміди.
Якщо користуються способом граней, то будують сторони фігури перерізу як лінії перетину площин граней із січною площиною. Так, відрізок прямої АВ являє собою лінію перетину грані 12S з площиною Г, ВС – грані 23S і АС – грані 13S.
Вибираючи той чи інший спосіб розв’язування, необхідно керуватися міркуваннями про найпростіше розв’язування задачі. Слід також мати на увазі, що якщо січна площина є проекціюючою, то одна з проекцій фігури перерізу збігається із слідом цієї площини, і задача зводиться до побудови другої її проекції за однією відомою.
Розглянемо кілька прикладів на застосування обох способів.
Перетин площини з багатогранником
Приклад 1. Побудувати натуральний вигляд перерізу прямої призми фронтально – проекціюючою площиною Σ.
Фігура перерізу – трикутник. Фронтальна її проекція збігається зі слідом січної площини Σ, а горизонтальна – з однойменною проекцією призми. Натуральний вигляд перерізу А4В4С4 побудований на новій горизонтальній площині проекцій p4, паралельній площині перерізу.
Приклад 2. Побудувати проекції перерізу трикутної піраміди фронтально – проекціюючою площиною Σ.
Площина Σ перетинає піраміду по трикутнику АВС. Його фронтальна проекція А2В2С2 збігається з однойменним слідом Σ2 січної площини. Горизонтальні проекції вершин А і С побудовані за допомогою ліній проекційного зв’язку, а вершини В, яка лежить на профільному ребрі 2S, – за допомогою горизонталі h грані 23S.
Перетин прямої лінії з багатогранником
Загальним способом побудови точок перетину прямої з поверхнею багатогранника здійснюють в такій послідовності:
– через пряму проводять допоміжну площину;
– будують багатокутник, по якому допоміжна площина перетинає багатогранник;
– фіксують точки перетину прямої з фігурою перерізу, які і є шуканими точками.
Приклад 1. Побудувати точки перетину прямої l з поверхнею трикутної піраміди.
Через пряму провели фронтально – проекціюючу площину Σ, яка перетинає піраміду по трикутнику АВС. Шукані точки перетину М та N.
Перетин кривих поверхонь площиною та прямою лінією
В загальному випадку лінію перетину кривої поверхні з площиною будують способом допоміжних січних площин.
Січна площина Г перетинає задану поверхню Ф по деякій лінії l. Точки цієї лінії будують за допомогою допоміжних площин. Так, площина Σ перетинає задану поверхню по кривій лінії и, а січну площину Г – по прямій а. Ці лінії перетинаються в точках М і N, які належать шуканій лінії перетину l. Повторюючи указаний спосіб декілька разів, можна знайти достатню кількість точок для побудови фігури перерізу. При цьому допоміжні площини слід вибирати так, щоб одержувались прості перерізи поверхні.
Якщо поверхня лінійчата, то фігуру перерізу можна будувати способом твірних, визначаючи точки перетину прямолінійних твірних з січною площиною. Таким чином, побудова ліній перетину зводиться до багаторазового розв’язування відомої задачі про визначення точки перетину прямої з площиною.
Перетин циліндра площиною
Площина може перетинати циліндр по прямолінійних твірних, по колу і по еліпсу.
Приклад 1. Побудувати проекції і натуральний вигляд перерізу прямого кругового циліндра фронтально – проекціюючою площиною Σ.
Фігура перерізу – еліпс. Фронтальна проекція його збігається із Σ2, а горизонтальна – з колом, в яке проектується на площину p1 циліндр.
Велика вісь еліпса визначається відрізком АВ, а мала СD дорівнює діаметру циліндра d. Натуральний вигляд перерізу знайдено двома способами – способом плоскопаралельного переміщення і способом заміни площин проекцій.
Перетин конуса площиною
Можливі такі перерізи конуса:
1. Еліпс, якщо січна площина перетинає всі твірні конуса.
2. Парабола, якщо січна площина паралельна одній твірній конуса.
3. Гіпербола, якщо січна площина паралельна двом твірним конуса.
4. Трикутник, якщо січна площина проходить через вершину конуса.
На рис. 17, а дана фронтальна проекція прямого кругового конуса і показані сліди січних площин, які дають відповідні перерізи, а на рис. 17, б, в, г, д, е – наведені їх наочні зображення.
Перетин кривих поверхонь прямою лінією
Загальним способом побудови точок перетину прямої лінії з поверхнею виконують в такій послідовності:
– через пряму проводять допоміжну площину;
– будують лінію перетину поверхні допоміжною площиною;
– визначають точки перетину прямої з поверхнею.
Висновки по третьому питанню:
1. Побудова багатокутника перерізу зводиться до розв’язування відомих позиційних задач: побудова точки перетину прямої з площиною або лінії перетину двох площин.
2. Відповідно розрізняють два способи побудови: спосіб ребер і спосіб граней. Використовуючи спосіб ребер, визначають вершини багатокутника перерізу як точки перетину ребер багатогранника з січною площиною. Якщо користуються способом граней, то будують сторони фігури перерізу як лінії перетину площин граней із січною площиною.
Похожие работы
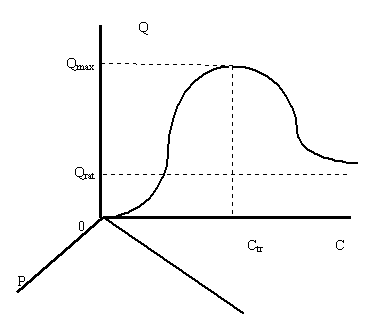
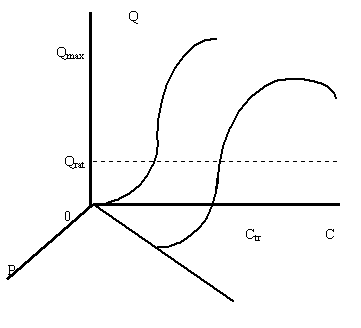
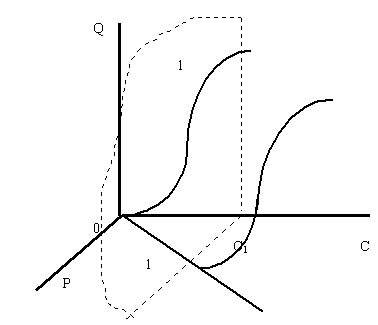
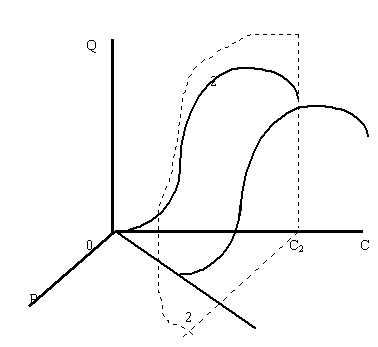
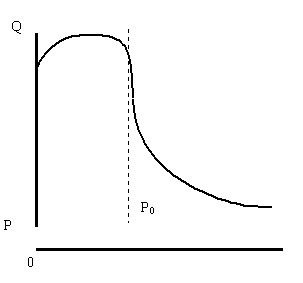
... спроса плоскостью с постоянным доходом С1 При небольшой величине дохода С1 плоскость постоянных доходов, обозначенная на рисунке 3 цифрами 1 с краями, изображенными пунктирными линиями, пересекает поверхность спроса перпендикулярно оси доходов и параллельно плоскости цена-объем. В результате пересечения плоскости и поверхности спроса получается кривая спроса, имеющая классический вид. Можно с ...
... растет как 1-D, но D = DBL при подходе Минковского и D = DCL > DBL при использовании измерительного циркуля. Может ли размерность D принимать значения, отличающиеся от этих двух величин? 5. Измерение площади самоаффинных фрактальных поверхностей, полученных из графиков функций 5.1. Площадь фрактального рельефа ВH (х, у), найденная с помощью «шарфа» Минковского Мы возвращаемся к размерностям ...
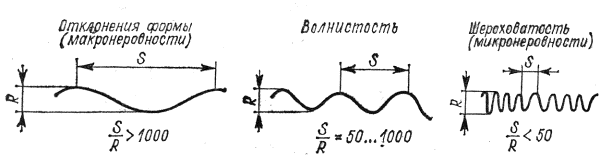
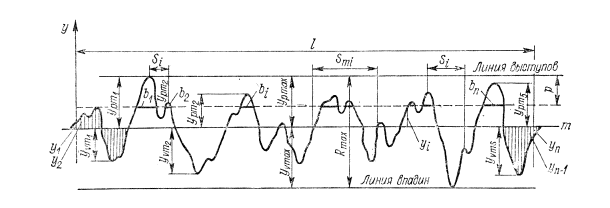
... шероховатости поверхностей, установленные ГОСТ 2789-73. Обозначение шероховатости поверхностей и правила их нанесения на чертеже установлены ГОСТ 2309-73. Структура обозначения шероховатости приведена на Рис.6 Рис.6 Структура знака для изображения шероховатости поверхности При установлении требований шероховатости поверхности рекомендуется применять параметры Ra, Rz, Rmax, tp. ...
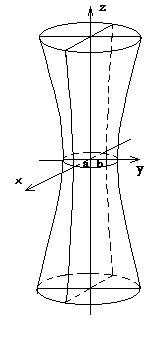
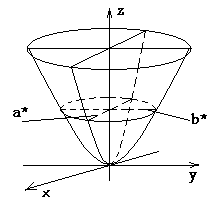
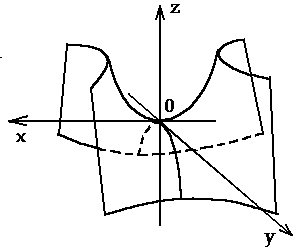
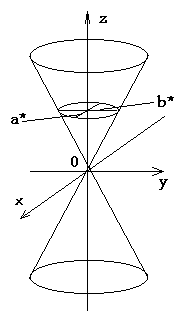
... которых следует, что при h>0 в сечении получаются гиперболы, пересекающие плоскость Oxy; при h<0 – гиперболы, пересекающие плоскости Oyz; при h=0 – гипербола вырождается в пару пересекающихся прямых и точка (0;0;0) называется вершиной параболоида; числа p и q – его параметрами. 6. Конус второго порядка. Конусом второго порядка называется поверхность, которая в некоторой

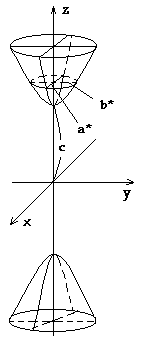
0 комментариев