Навигация
Взаємний перетин поверхонь тіл. Побудова лінії перетину поверхонь. Спосіб допоміжних січних поверхонь
4. Взаємний перетин поверхонь тіл. Побудова лінії перетину поверхонь. Спосіб допоміжних січних поверхонь
Більшість найскладніших і відповідальних оригінальних деталей приладів і машин утворені комбінацією різних елементарних тіл, розташованих у просторі так, що поверхні їх перетинаються між собою. Тому важливим етапом конструювання таких деталей є визначення меж елементарних початкових поверхонь, якими і є лінії їхнього взаємного перетину.
Спільна лінія двох поверхонь називається лінією їх перетину.
Для побудови лінії перетину поверхонь використовують два способи та їх комбінації.
1. Будують точки перетину ребер одного багатогранника з грянями другого і ребер другого з гранями першого. Через побудовані точки в певній послідовності проводять ламану лінію перетину даних багатогранників. При цьому відрізки прямих проводять лише через ті побудовані точки, які лежать у одній і тій же грані.
2. Будують відрізки прямих, по яких грані однієї поверхні перетинають грані другої. Ці відрізки є ланками ламаної лінії перетину багатогранних поверхонь між собою.
3. Таким чином, побудова перетину двох багатогранників зводиться аж до побудови лінії перетину двох площин між собою, або до побудови точки перетину прямої з площиною. На практиці, як правило, використовують обидва способи в комбінації, виходячи з умови простоти і зручності побудови.
Загальний спосіб побудови лінії перетину двох поверхонь називається способом допоміжних січних поверхонь або способом посередників. Суть цього способу полягає у наступному.
Дві криволінійні поверхні перетинаються третьою допоміжною січною площиною. Знаходять лінії перетину KL та MN допоміжні поверхні з кожною із заданих. Точка перетину побудованих ліній перетину KL та MN належить шуканій лінії заданих поверхонь.
Повторюючи такі побудови багаторазово за допомогою інших допоміжних поверхонь, знаходять необхідну кількість спільних точок двох поверхонь для проведення лінії їх перетину. Одержані точки з’єднують плавною кривою лінією.
Лінію перетину поверхонь називають також і лінією переходу даних поверхонь.
Загальне правило побудови лінії перетину поверхонь можна сформулювати так:
– вибрати тип допоміжних поверхонь;
– побудувати лінії перетину допоміжних поверхонь із заданими поверхнями;
– знайти точки перетину побудованих ліній і з’єднати їх між собою.
За допоміжні січні поверхні вибирають такі, лінії перетину яких із заданими поверхнями проекціюються на креслення в графічно прості лінії – прямі, кола. Такими посередниками є площини частинного положення, які паралельні площинам p1 і p2, або сфери. Щоб розв’язати задачу, треба провести не одну, а кілька допоміжних площин або сфер.
На прикладі бачимо:
– задані поверхні, наприклад a і β, перетинають допоміжною поверхнею γ;
– будують лінії перетину a і b поверхонь допоміжною поверхнею γ;
– точки перетину K та M лінії a з лінією b належать як a, так і β;
– повторюють попередні операції декілька разів, переміщуючи січну поверхню;
– будують лінію перетину поверхонь a і β, з’єднуючи отримані точки між собою.
На лінії перетину поверхонь розрізняють точки опорні і випадкові або проміжні.
Розпочинати побудову лінії перетину слід з визначення опорних точок: найвищих і найнижчих, крайніх правих і лівих, точок видимості тощо. Опорні точки дають можливість побачити, в яких межах розміщені проекції лінії перетину і де слід визначати проміжні точки.
Два тіла можуть перетинатися по одній або по двох замкнених лініях. У першому випадку перетин буде неповним і на тілах утворяться заглибини у вигляді врубок. Цей випадок називається врізанням. При двох замкнених лініях перетину одне тіло цілком проникає в інше. Такий випадок називається проникненням.
Характер лінії перетину залежить від того які геометричні тіла або поверхні перетинаються.
Після того як за допомогою посередників визначені точки, які належать лінії перетину даних поверхонь, необхідно встановити послідовність з’єднання одержаних точок і визначити видимість окремих частин ліній перетину.
При визначенні послідовності з’єднання точок користуються такими положеннями:
– з’єднувати між собою можна лише такі точки, які лежать на одній і тій же грані кожної з двох поверхонь;
– з’єднувати між собою можна лише точки, які лежать на сусідніх твірних.
Але реалізація цих положень на практиці в ряді випадків викликає значні труднощі, вимагає великої затрати часу і добре розвинутої просторової уяви.
Визначивши точки лінії перетину, їх з’єднують в певній послідовності з врахуванням видимості окремих частин лінії перетину.
При цьому керуються такими положеннями:
1) якщо відрізок лінії перетину двох багатогранників лежить на перетині видимих граней даних проекцій фігур, то він також видимий на цій проекції;
2) якщо обидві грані або одна з них невидимі, то і відрізок лінії перетину даних граней невидимий;
3) для кривих поверхонь видимими є лише точки, одержані в перетині двох видимих твірних. Якщо одна з двох твірних невидима, то й точка перетину їх невидима;
4) точки переходу видимої частини лінії перетину в невидиму завжди лежать на обрисних твірних тієї чи іншої поверхні;
5) видимість визначається окремо для кожної з проекцій фігур, які перетинаються.
Література
1. Інженерна та комп’ютерна графіка: Методичні рекомендації для виконання графічних робіт при курсовому та дипломному проектуванні /Укл. Є.В. Перегуда. – Житомир: ВФРЕ при ЖІТІ, 1998. – 84 с.
2. Годік Є.І. Технічне креслення. – М.: Машинобудування, 1974. – 320 с.
3. Хаскін А.М. Креслення. – К.: Вища школа, 1972.
4. Гордон В.О., Семенцов-Огиевский М.А. Курс начертательной геометрии. М., 1988. – 272 с.
Похожие работы
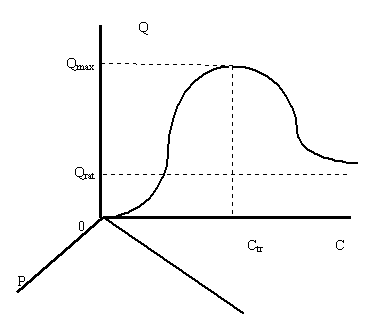
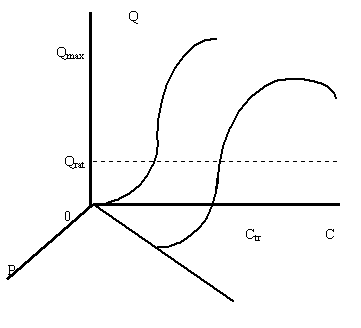
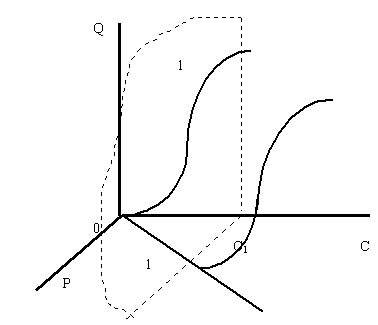
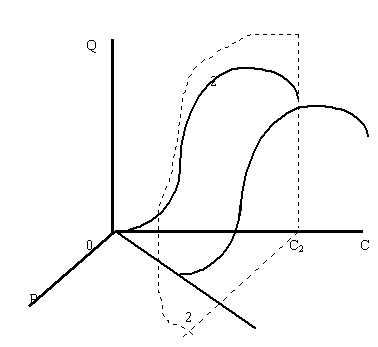
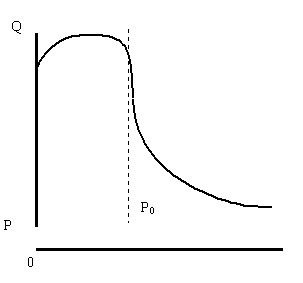
... спроса плоскостью с постоянным доходом С1 При небольшой величине дохода С1 плоскость постоянных доходов, обозначенная на рисунке 3 цифрами 1 с краями, изображенными пунктирными линиями, пересекает поверхность спроса перпендикулярно оси доходов и параллельно плоскости цена-объем. В результате пересечения плоскости и поверхности спроса получается кривая спроса, имеющая классический вид. Можно с ...
... растет как 1-D, но D = DBL при подходе Минковского и D = DCL > DBL при использовании измерительного циркуля. Может ли размерность D принимать значения, отличающиеся от этих двух величин? 5. Измерение площади самоаффинных фрактальных поверхностей, полученных из графиков функций 5.1. Площадь фрактального рельефа ВH (х, у), найденная с помощью «шарфа» Минковского Мы возвращаемся к размерностям ...
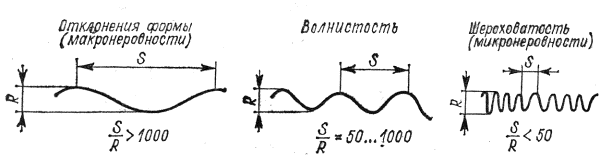
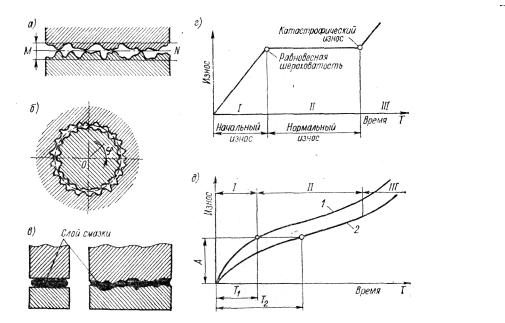
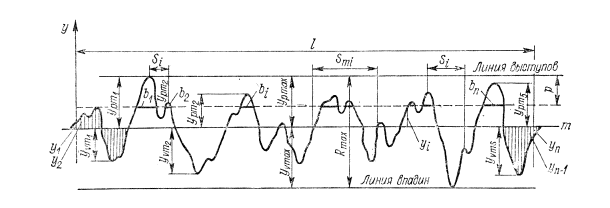
... шероховатости поверхностей, установленные ГОСТ 2789-73. Обозначение шероховатости поверхностей и правила их нанесения на чертеже установлены ГОСТ 2309-73. Структура обозначения шероховатости приведена на Рис.6 Рис.6 Структура знака для изображения шероховатости поверхности При установлении требований шероховатости поверхности рекомендуется применять параметры Ra, Rz, Rmax, tp. ...
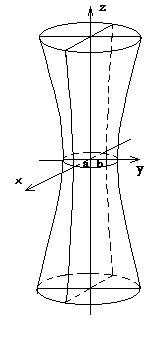
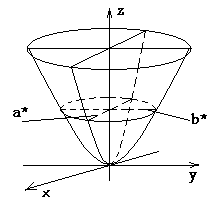
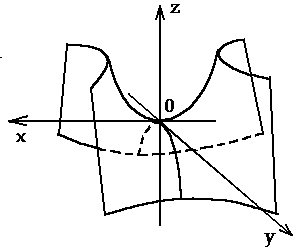
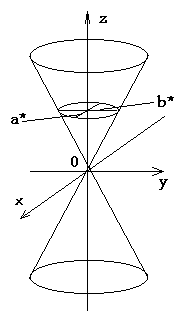
... которых следует, что при h>0 в сечении получаются гиперболы, пересекающие плоскость Oxy; при h<0 – гиперболы, пересекающие плоскости Oyz; при h=0 – гипербола вырождается в пару пересекающихся прямых и точка (0;0;0) называется вершиной параболоида; числа p и q – его параметрами. 6. Конус второго порядка. Конусом второго порядка называется поверхность, которая в некоторой

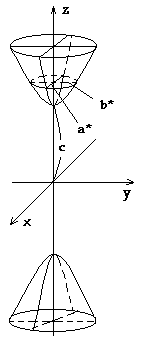
0 комментариев