Функция Эйлера

4 Функция Эйлера

 

Определение. Функция : R R (или, более общо, : C C ) называется мультипликативной если:

1). Функция определена всюду на N и существует а N такой, что ( а ) 0.

2). Для любых взаимно простых натуральных чисел а ₁ и а ₂ выполняется ( а ₁ · а ₂ ) = ( а ₁ ) · ( а ₂ ).

Пример 1. ( а ) = а ^s , где s - любое (хоть действительное, хоть комплексное) число. Проверка аксиом 1) и 2) из определения мультипликативной функции не составляет труда, а сам пример показывает, что мультипликативных функций по меньшей мере континуум, т.е. много.

Перечислим, кое-где доказывая, некоторые свойства мультипликативных функций. Пусть всюду ниже ( а ) - произвольная мультипликативная функция.

Свойство 1. (1) = 1.

Доказательство. Пусть а - то самое натуральное число, для которого

( а ) 0. Тогда ( а · 1) = ( а ) · (1) = ( а ).

 

Свойство 2.

,

где р ₁ , р ₂ ,..., р _n - различные простые числа.

Доказательство очевидно.

Свойство 3. Обратно, мы всегда построим некоторую мультипликативную функцию ( a ), если зададим (1) = 1 и произвольно определим ( р ) для всех простых р и всех натуральных , а для остальных натуральных чисел доопределим функцию ( a ) используя равенство

.

 

Доказательство сразу следует из основной теоремы арифметики.

Пример 2. Пусть (1) = 1 и ( р ) = 2 для всех р и . Тогда, для произвольного числа,

.

 

Свойство 4. Произведение нескольких мультипликативных функций является мультипликативной функцией.

Доказательство. Сначала докажем для двух сомножителей: Пусть ₁ и ₂ - мультипликативные функции = ₁ · ₂ , тогда (проверяем аксиомы определения)

1) (1) = ₁ (1) · ₂ (1) = 1 и, кроме того, существует такое a (это a = 1), что ( a ) 0.

2) Пусть ( a , b ) = 1 - взаимно просты. Тогда

( a · b ) = ₁ ( a · b ) · ₂ ( a · b ) =

= ₁ ( a ) ₁ ( b ) ₂ ( a ) ₂ ( b ) =

= ₁ ( a ) ₂ ( a ) · ₁ ( b ) ₂ ( b ) = ( a ) ( b ).

Доказательство для большего числа сомножителей проводится стандартным индуктивным рассуждением.



Введем удобное обозначение. Всюду далее, символом

будем обозначать сумму чего-либо, в которой суммирование проведено по всем делителям d числа n . Следующие менее очевидные, чем предыдущие, свойства мультипликативных функций я сформулирую в виде лемм, ввиду их важности и удобства дальнейших ссылок.

Лемма 1. Пусть

- каноническое разложение числа a N , - любая мультипликативная функция. Тогда:

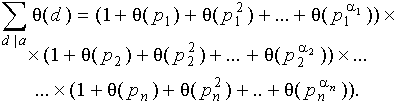
Если a = 1, то считаем правую часть равной 1.

Доказательство. Раскроем скобки в правой части. Получим сумму всех (без пропусков и повторений) слагаемых вида

,

где 0 _k _k , для всех k n . Так как различные простые числа заведомо взаимно просты, то

,

а это как раз то, что стоит в доказываемом равенстве слева.



Лемма 2. Пусть ( a ) - любая мультипликативная функция. Тогда

,

- также мультипликативная функция.

Доказательство. Проверим для ( a ) аксиомы определения мультипликативной функции.

1).

2). Пусть

и все р и q различны. Тогда, по предыдущей лемме, имеем: (благо, делители у чисел a и b различны)



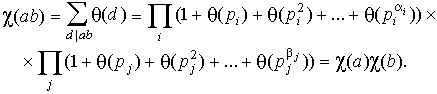
Пример 1. Число делителей данного числа.

Пусть ( а ) = а ⁰ 1 - тождественная единица (заведомо мультипликативная функция). Тогда, если

,

то тождество леммы 1 пункта 13 принимает вид:

,

- это не что иное, как количество делителей числа a . По лемме 2 пункта 13, количество делителей ( a ) числа a есть мультипликативная функция.

Пример 2. Сумма делителей данного числа.

Пусть ( a ) = a ¹ a - тождественная мультипликативная функция. Тогда, если

,

то тождество леммы 1 пункта 13 принимает вид:

сумма первых ( + 1) членов геометрической прогрессии

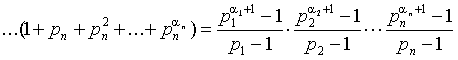
- сумма всех делителей числа a . По лемме 2 пункта 13, сумма всех делителей есть мультипликативная функция.

Пример 3. Функция Мебиуса.

Функция Мебиуса ( a ) - это мультипликативная функция, определяемая следующим образом: если p - простое число, то ( p ) = -1; ( p ) = 0, при > 1; на остальных натуральных числах функция доопределяется по мультипликативности.

Таким образом, если число a делится на квадрат натурального числа, отличный от единицы, то ( a ) = 0; если же a = p ₁ p _{2· · ·} p _n (теоретик-числовик сказал бы на своем жаргоне: "если a свободно от квадратов"), то ( a ) = (-1) ^k , где k - число различных простых делителей a . Понятно, что (1) = (-1) ⁰ = 1, как и должно быть.

Лемма 1. Пусть ( a ) - произвольная мультипликативная функция,

.

Тогда:

(при a = 1 считаем правую часть равной 1).

Доказательство. Рассмотрим функцию ₁ ( x ) = ( x ) · ( x ). Эта функция мультипликативна, как произведение мультипликативных функций. Для ₁ ( x ) имеем ( p - простое): ₁ ( p ) = - ( x ); ₁ ( p ) = 0, при > 1. Следовательно, для ₁ ( x ) тождество леммы 1 пункта 13 выглядит так:



 

Следствие 1. Пусть ( d ) = d ^-1 = 1/ d (это, конечно, мультипликативная функция),

Тогда:

 

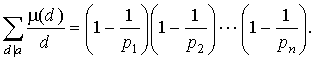
Пример 4. Функция Эйлера.

Функция Эйлера, пожалуй, самая знаменитая и "дары приносящая" функция из всех функций, рассматриваемых в этом пункте. Функция Эйлера ( a ) есть количество чисел из ряда 0, 1, 2,..., a - 1, взаимно простых с a . Полезность и практическое применение этой функции я продемонстрирую в следующих пунктах, а сейчас давайте поймем, как ее вычислять.

Лемма 2. Пусть

.

Тогда:

1) 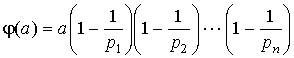(формула Эйлера);

2)

в частности, ( p ^) = p ^- p ^-1 , ( p ) = p - 1.

Доказательство. Пусть x пробегает числа 0, 1, 2,..., a - 1. Положим _x = ( x , a ) - наибольший общий делитель. Тогда ( a ) есть число значений _x , равных 1. Придумаем такую функцию ( _x ), чтобы она была единицей, когда _x единица, и была нулем в остальных случаях. Вот подходящая кандидатура:

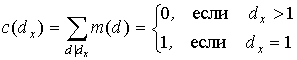
Последнее легко понять, если вспомнить лемму 1 из этого пункта и в ее формулировке взять ( d ) 1. Далее, сделав над собой некоторое усилие, можно усмотреть, что:

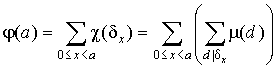
Поскольку справа сумма в скобках берется по всем делителям d числа _x = ( x , a ), то d делит x и d делит a . Значит в первой сумме справа в суммировании участвуют только те x , которые кратны d . Таких x среди чисел 0, 1, 2,..., a - 1 ровно a / d штук. Получается, что:

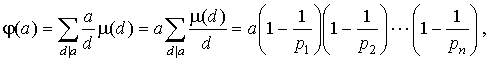
что и требовалось.

Пояснение для читателей, у которых предыдущие соображения не захотели укладываться в голову, например, из-за плохих погодных условий. Имеем

Зафиксируем некоторое d ₀ такое, что d ₀ делит a , d ₀ делит x , x < a . Значит в сумме справа в скобках слагаемых ( d ₀ ) ровно a / d ₀ штук и ( a ) есть просто сумма

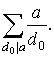
После этого, равенство

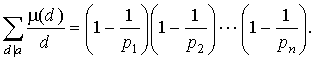
получается применением следствия из леммы 1 этого пункта. Должен признать, что приведенное доказательство формулы Эйлера и, в особенности, его последний момент с изменением порядка суммирования, объективно тяжеловаты для понимания. Но мы не боимся трудностей!

Второе утверждение леммы следует из первого внесением впереди стоящего множителя a внутрь скобок.

Оказывается, только что доказанная формула

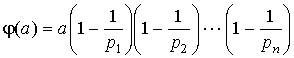
для вычисления функции Эйлера имеет ясный "физический смысл". Дело в том, что в ней отражено так называемое правило включений и исключений:

Правило включений и исключений. Пусть задано множество А и выделено k его подмножеств. Количество элементов множества А , которые не входят ни в одно из выделенный подмножеств, подсчитывается так: надо из общего числа элементов А вычесть количества элементов всех k подмножеств, прибавить количества элементов всех их попарных пересечений, вычесть количества элементов всех тройных пересечений, прибавить количества элементов всех пересечений по четыре и т.д. вплоть до пересечения всех k подмножеств.

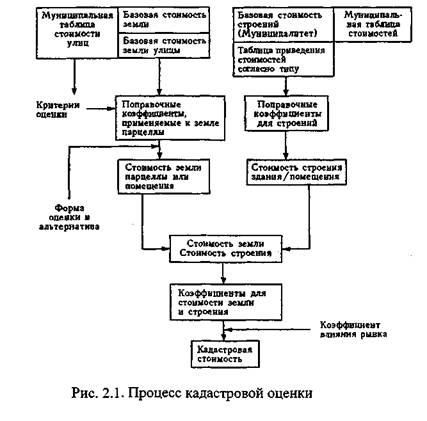
Проиллюстрирую это правило на примере подсчета функции Эйлера для чисел вида

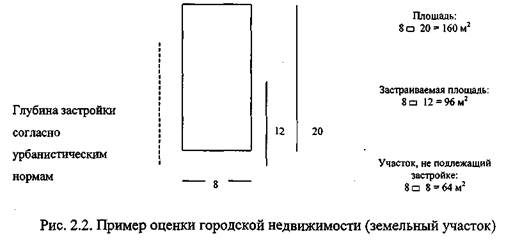
Посмотрите на рисунок 1.

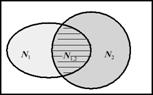
Рис. 1.

Прямоугольник изображает множество всех целых чисел от 0 до a ; овал N ₁ - множество чисел, кратных p ₁ ; кружок N ₂ - числа, кратные p ₂ ; пересечение N _1,2 - множество чисел, делящихся одновременно на p ₁ и p ₂ , т.е. на p ₁ p ₂ ; числа вне овала и кружочка взаимно просты с a . Для подсчета числа чисел, взаимно простых с a , нужно из a вычесть количество чисел в N ₁ и количество чисел в N ₂ (их, соответственно, a / p ₁ и a / p ₂ штук), при этом общая часть N _1,2 (там a /( p ₁ p ₂ ) штук чисел) вычтется дважды, значит ее надо один раз прибавить (вот оно, "включение - исключение"!). В результате получим:

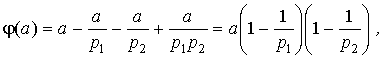
что я вам и утверждал. Мне кажется, что таким способом можно объяснить формулу Эйлера любому смышленому школьнику.

Кстати, любому смышленому школьнику вполне возможно объяснить и то, что при a > 2, ( a ) всегда число четное. Действительно, если k взаимно просто с a и k < a , то число a - k тоже меньше a , взаимно просто с a и не равно k . (Если бы a и a - k имели общий делитель, то их разность a - ( a - k ) = k тоже делилась бы на этот делитель, что противоречит взаимной простоте a и k .) Значит числа, взаимно простые с a разбиваются на пары k и a - k , следовательно, их четное число.

Из леммы 2 вытекают приятные следствия.

Следствие 2. Функция Эйлера мультипликативна.

Доказательство. Имеем:

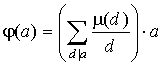
- произведение двух мультипликативных функций, первая из которых мультипликативна по лемме 2 пункта 13. Значит, ( a ) - мультипликативна.

 

Следствие 3. .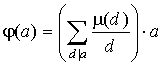

Доказательство. Пусть

.

Тогда, по лемме 1 пункта 13 имеем:

.

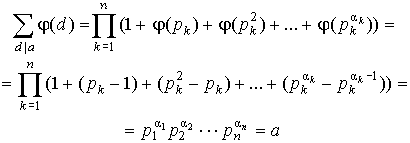5 Китайская теорема об остатках

В этом пункте детально рассмотрим только сравнения первой степени вида

ax b(mod m),

оставив более высокие степени на съедение следующим пунктам. Как решать такое сравнение? Рассмотрим два случая.

Случай 1. Пусть а и m взаимно просты. Тогда несократимая дробь m/a сама просится разложиться в цепную дробь:

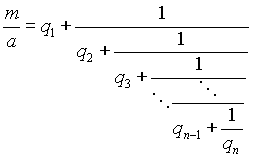
Эта цепная дробь, разумеется, конечна, так как m/a - рациональное число. Рассмотрим две ее последние подходящие дроби:

.

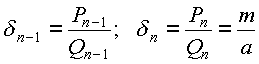Вспоминаем (пункт 9) важное свойство числителей и знаменателей подходящих дробей: mQ _n-1 -aP _n-1 =(-1) ⁿ . Далее (слагаемое mQ _n-1 , кратное m , можно выкинуть из левой части сравнения):

-aP _n-1 (-1) ⁿ (mod m) т.е.

aP _n-1 (-1) ^n-1 (mod m) т.е.

a[(-1) ^n-1 P _n-1 b] b(mod m)

и единственное решение исходного сравнения есть:

x (-1) ^n-1 P _n-1 b(mod m)

 

Пример. Решить сравнение 111x 75(mod 322).

Решение. (111, 322)=1. Включаем алгоритм Евклида:

322=11 · 2+100

111=100 · 1+11

100=11 · 9+1

11=1 · 11

(В равенствах подчеркнуты неполные частные.) Значит, n=4 , а соответствующая цепная дробь такова:

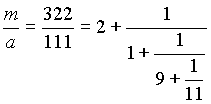
Посчитаем числители подходящих дробей, составив для этого стандартную таблицу:

	0	2	1	9	11
P n	1	2	3	29	322

Числитель предпоследней подходящей дроби равен 29, следовательно, готовая формула дает ответ: x (-1) ³ 29 75 -2175 79(mod 322)



Ох уж эти мне теоретико-числовые рассуждения из разных учебников, продиктованные традицией изложения и необходимостью обязательно использовать ранее изложенную теорию! О чем идет речь в нескольких строках выше? Дано сравнение ax b(mod m) , где a и m взаимно просты. Ну возьмите вы алгоритм Евклида, найдите те самые пресловутые u , v Z такие, что au+vm=1 , умножьте это равенство на b : aub+vmb=b , откуда немедленно следует: aub b(mod m) . Значит решением исходного сравнения является x ub(mod m) . Собственно, и все. Поворчал.

Случай 2. Пусть (a,m)=d . В этом случае, для разрешимости сравнения ax b(mod m) необходимо, чтобы d делило b , иначе сравнение вообще выполняться не может. Действительно, ax b(mod m) бывает тогда, и только тогда, когда ax- b делится на m нацело, т.е. ax- b=t · m ,

t Z , откуда b=ax- t m , а правая часть последнего равенства кратна d .

Пусть b=db ₁ , a=da ₁ , m=dm ₁ . Тогда обе части сравнения xa ₁ d b ₁ d(mod m ₁ d) и его модуль поделим на d :

xa ₁ b ₁ (mod m ₁ ) ,

где уже а ₁ и m ₁ взаимно просты. Согласно случаю 1 этого пункта, такое сравнение имеет единственное решение x ₀ :

x x ₀ (mod m ₁ ) (*)

По исходному модулю m , числа (*) образуют столько решений исходного сравнения, сколько чисел вида (*) содержится в полной системе вычетов: 0,1,2,..., m-2, m-1 . Очевидно, что из чисел x=x ₀ +t m в полную систему наименьших неотрицательных вычетов попадают только x ₀ , x ₀ +m ₁ , x ₀ +2m ₁ , ..., x ₀ +(d-1)m ₁ , т.е. всего d чисел. Значит у исходного сравнения имеется d решений.

Подведем итог рассмотренных случаев в виде следующей теоремы

Теорема 1. Пусть (a,m)=d . Если b не делится на d , сравнение ax b(mod m) не имеет решений. Если b кратно d , сравнение ax b(mod m) имеет d штук решений.

Пример. Решить сравнение 111x 75(mod 321) .

Решение. (111,321)=3 , поэтому поделим сравнение и его модуль на 3:

37x 25(mod 107) и уже (37,107)=1 .

Включаем алгоритм Евклида (как обычно, подчеркнуты неполные частные):

107=37 2+33

37=33 1+4

33=4 8+1

4=1 4

Имеем n=4 и цепная дробь такова:

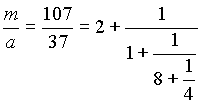
Таблица для нахождения числителей подходящих дробей:

q n	0	2	1	8	4
P n	1	2	3	26	107

Значит, x (-1) ³ 26 25 -650(mod 107) -8(mod 107) 99(mod 107) .

Три решения исходного сравнения:

x 99(mod 321), x 206(mod 321), x 313(mod 321) ,

и других решений нет.

Теорема 2. Пусть m>1, (a,m)=1 Тогда сравнение ax b(mod m) имеет решение: x ba ^(m)-1 (mod m) .

Доказательство. По теореме Эйлера, имеем: a ^(m) 1(mod m) , следовательно, a ba ^(m)-1 b(mod m) .

Пример. Решить сравнение 7x 3(mod 10) . Вычисляем:

(10)=4; x 3 7 ^4-1 (mod 10) 1029(mod 10) 9(mod 10) .

Видно, что этот способ решения сравнений хорош (в смысле минимума интеллектуальных затрат на его осуществление), но может потребовать возведения числа а в довольно большую степень, что довольно трудоемко. Для того, чтобы как следует это прочувствовать, возведите самостоятельно число 24789 в степень 46728.

Теорема 3. Пусть р – простое число, 0<a<p . Тогда сравнение ax b(mod p) имеет решение:

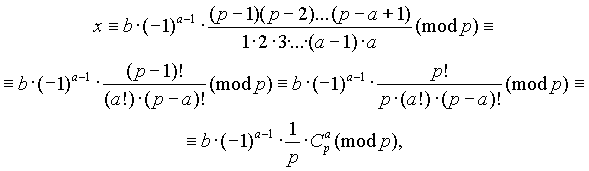
где C _a ^p – биномиальный коэффициент.

Доказательство непосредственно следует из очевидного сравнения

которое нужно почленно поделить на взаимно простое с модулем число 1 2 3 ... a-1 .

Пример. Решить сравнение 7x 2(mod 11) . Вычисляем:

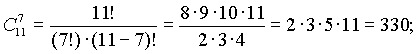
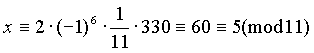
На этом пункт 19 можно было бы и закончить, но невозможно, говоря о решении сравнений первой степени, обойти стороной вопрос о решении систем сравнений первой степени. Дело в том, что умение решать простейшие системы сравнений не только является неотъемлемой частью общечеловеческой культуры, позволяющей гражданину не падать в ямы, расщелины и открытые люки. Такое умение, кроме всего прочего, пригодится нам при изучении сравнений произвольной степени, о которых пойдет речь в следующих пунктах.

Лемма 1 (Китайская теорема об остатках). Пусть дана простейшая система сравнений первой степени:

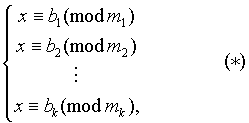
где m ₁ ,m ₂ ,...,m _k попарно взаимно просты. Пусть, далее, m ₁ m ₂ ...m _k =M _s m _s ; M _s M _s ^1(mod m _s ) (Очевидно, что такое число M _s ^всегда можно подобрать хотя бы с помощью алгоритма Евклида, т.к. (m _s ,M _s )=1 ); x ₀ =M ₁ M ₁ ^b ₁ +M ₂ M ₂ ^b ₂ +...+M _k M _k ^b _k . Тогда система (*) равносильна одному сравнению

x x ₀ (mod m ₁ m ₂ ...m _k ) ,

т.е. набор решений (*) совпадает с набором решений сравнения x x ₀ (mod m ₁ m ₂ ...m _k ) .

Доказательство. Имеем: m _s делит M _j , при s j. Следовательно, x ₀ M _s M _s ^b _s (mod m _s ) , откуда x ₀ b _s (mod m _s ) . Это означает, что система (*) равносильна системе

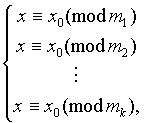
которая, очевидно, в свою очередь, равносильна одному сравнению x x ₀ (mod m ₁ m ₂ ...m _k ) .

В следующей лемме, для краткости формулировки, сохранены обозначения леммы 1.

Лемма 2. Если b ₁ ,b ₂ ,...,b _k пробегают полные системы вычетов по модулям m ₁ ,m ₂ ,...,m _k соответственно, то x ₀ пробегает полную систему вычетов по модулю m ₁ m ₂ ...m _k .

Доказательство. Действительно, x ₀ =A ₁ b ₁ +A ₂ b ₂ +...+A _k b _k пробегает m ₁ m ₂ ...m _k различных значений. Покажем, что все они попарно не сравнимы по модулю m ₁ m ₂ ...m _k .

Ну пусть оказалось, что

A ₁ b ₁ +A ₂ b ₂ +...+A _k b _k A ₁ b' ₁ +A ₂ b' ₂ +...+A _k b' _k (mod m ₁ m ₂ ...m _k )

 

Значит,

A ₁ b ₁ +A ₂ b ₂ +...+A _k b _k A ₁ b' ₁ +A ₂ b' ₂ +...+A _k b' _k (mod m _s )

для каждого s , откуда

M _s M _s ^b _s M _s M _s ^b' _s

Вспомним теперь, что M _s M _s ^1(mod m _s ) , значит M _s M _s ^1+m _s t , откуда (M _s M _s ^,m _s )=1 . Разделив теперь обе части сравнения

M _s M _s ^b _s M _s M _s ^b' _s

на число M _s M _s ^, взаимно простое с модулем, получим, что b _s b' _s (mod m _s ) , т.е. b _s =b' _s для каждого s .

Итак, x ₀ пробегает m ₁ m ₂ ...m _k различных значений, попарно не сравнимых по модулю m ₁ m ₂ ...m _k , т.е. полную систему вычетов.

Формулировка для колец

Пусть - коммутативные ассоциативные кольца с единицей, сюрьективные гомоморфизмы, обладающие свойством для всех . Тогда гомоморфизм , заданный формулой

является сюрьективным. Более того, Φ опеределяет изоморфизм

.

Если положить , и определить гомоморфизмы следующим образом

то мы получим арифметическую версию теоремы.

Также часто встречается следующая эквивалентная формулировка для колец, где B_i имеют форму A / I_i, φ_i являются естественными проекциями на A / I_i и требуется, чтобы I_i + I_j = A для любых .

Заключение

История арифметики остатков начинается с исследований К.Ф. Гаусса, который впервые стал рассматривать сравнения. В дальнейшем была обнаружена связь теории сравнений с астрономическими задачами (китайская теорема об остатках). В результате многочисленных исследований теория остатков была распространена на кольца произвольной природы. В последнее время обнаружилось приложение этой теории в криптографии. В дипломной работе изложена теория остатков на современном алгебраическом языке.

Список использованных источников

1.  С. Ленг, Алгебра, М., 1968

2.  С. Коунтинхо, Введение в теорию чисел. Алгоритм RSA, М. 2001

3.  А.И. Кострикин, Введение в алгебру, М., 2000

4.  О. Зарисский, Коммутативная алгебра, т.1., М., 1963