Статистический анализ выборочной совокупности

4.  Статистический анализ выборочной совокупности

Выборочной совокупностью, или просто выборкой, называют совокупность случайно отобранных объектов. Объемом n выборочной совокупности называют число объектов этой совокупности.

Интервальным статистическим распределением выборки называют перечень интервалов и соответствующих им частот n_i или относительных частот .

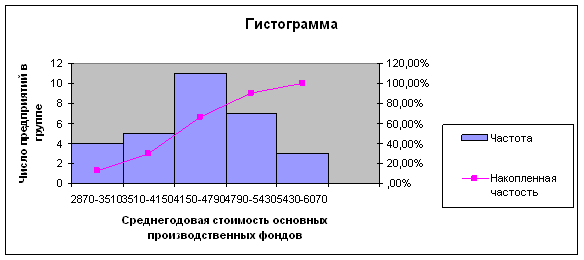
Гистограммой частот называют ступенчатую фигуру, состоящую из прямоугольников, основаниями которых служат частичные интервалы длиной h, а высоты равны отношению  (плотность частоты).

Гистограммой относительных частот называют ступенчатую фигуру, состоящую из прямоугольников, основаниями которых служат частичные интервалы длиною h, а высоты равны отношению  (плотность относительной частоты).

Для распределения наблюдений по интервалам необходимо найти длину интервала h, определяемую как отношение разности между максимальным X_maх и минимальным X_min элементами выборки к количеству интервалов k

. (15)

Количество интервалов k (целое число) целесообразно выбрать не менее 7, но и не более 15 или определить по формуле Старджесса

, (16)

где n – объем выборки.

Если k, вычисляемое по формуле Старджесса, нецелое число, то в качестве числа интервалов можно ближайшее к k целое число, не меньшее k.

Статистические оценки параметров распределения

Выборочной средней  называют среднее арифметическое значение признака выборочной совокупности. Если все значения х₁, х₂, …., х_n выборки объема n различны, то

.

Если значения признака х₁, х₂, …., х_k имеют соответственно частоты n₁, n₂, …..n_k, причем n₁+n₂+……+n_k=n, то

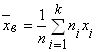. (17)

Для характеристики рассеяния значений количественного признака Х выборки вокруг своего среднего значения вводят такой параметр как выборочная дисперсия.

Выборочной дисперсией D_в называют среднее арифметическое квадратов отклонения наблюдаемых значений признака от их среднего значения . Если все значения х₁, х₂, …., х_n признака различны, то

=

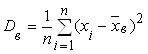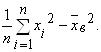
Если значения признака х₁, х₂, …., х_k имеют соответственно частоты n₁, n₂, …..n_k, причем n₁+n₂+……+n_k=n, то

. (18)

Выборочным средним квадратическим отклонением называют квадратный корень из выборочной дисперсии:

. (19)

Начальный эмпирический момент  порядка s статистического распределения определяют по формуле

, (20)

где x_i – наблюдаемое значение признака, n_i – частота наблюдаемого значения признака, n – объем выборки.

Начальный эмпирический момент первого порядка равен выборочной средней .

Центральный эмпирический момент  порядка s статистического распределения определяют по формуле

.

Центральный эмпирический момент второго порядка равен выборочной дисперсии .

Коэффициент асимметрии  статистического распределения определяется по формуле

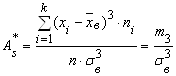. (22)

Эксцесс  статистического распределения определяется по формуле

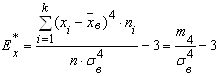. (23)

Относительной характеристикой рассеивания случайной величины выступает коэффициент вариации V, который вычисляется как отношение среднего квадратического отклонения и выборочной средней по формуле

. (24)

Метод моментов

Метод моментов – это определение неизвестных параметров статистического распределения путем приравнивания теоретических моментов рассматриваемого распределения соответствующим эмпирическим моментам того же порядка.

Для нахождения параметра λ показательного распределения необходимо приравнять начальный момент первого порядка показательного распределения начальному моменту первого порядка эмпирического распределения:

 (25)

Для нахождения параметров а и σ нормального распределения необходимо:

1) приравнять начальный момент первого порядка нормального распределения к начальному моменту первого порядка эмпирического распределения:

; (26)

2)  центральный момент второго порядка нормального распределения к центральному моменту второго порядка эмпирического распределения:

. (27)

Для нахождения параметров a и b равномерного распределения необходимо:

1) приравнять начальный момент первого порядка равномерного распределения к начальному моменту первого порядка эмпирического распределения:

;

2) центральный момент второго порядка равномерного распределения к центральному моменту второго порядка эмпирического распределения:

.

Параметры равномерного распределения a и b можно определить по формулам

 (28)

. (29)

Начальные эмпирические моменты третьего  и четвертого  порядков статистического распределения приравниваются соответственно к начальным моментам третьего  и четвертого  порядков случайной величины:  и .

Центральные эмпирические моменты третьего  и четвертого  порядков статистического распределения приравниваются соответственно к центральным моментам третьего  и четвертого  порядков случайной величины:  и .

Проверка статистических гипотез

Установление закона распределения выборочной совокупности проводится через проверку статистических гипотез.

Статистической называют гипотезу о виде неизвестного распределения. Статистические гипотезы бывают двух видов: нулевая (выдвигаемая) гипотеза Н₀и конкурирующая (противоречащая нулевой) Н₁.

Проведение проверки статистическими методами приводит к появлению ошибок двух родов: 1) ошибка первого рода – отвержение правильной гипотезы; 2) ошибка второго рода – принятие неправильной гипотезы.

Вероятность совершить ошибку первого рода называют уровнем значимости и обозначают через α. Наиболее часто уровень значимости принимают 0,05, что означает наличие риска отвергнуть правильную гипотезу в пяти случаях из ста.

Для проверки нулевой гипотезы используется специально подобранная случайная величина, которая называется статистическим критерием.

Наблюдаемым значением критерия называют его значение, вычисленное по выборке.

После выбора определенного критерия множество всех его возможных значений разбивают на два непересекающихся подмножества: одно из них содержит значения критерия, при которых нулевая гипотеза отвергается, а другое – при которых она принимается.

Критической областью называют совокупность значений критерия, при которых нулевую гипотезу отвергают.

Областью принятия гипотезы называют совокупность значений критерия, при которых нулевую гипотезу принимают.

Критической точкой называют точку, отделяющую критическую область от области принятия гипотезы. Для каждого критерия имеются соответствующие таблицы, по которым и находят критическую точку.

Основной принцип проверки статистических гипотез формулируется следующим образом: если наблюдаемое значение критерия принадлежит критической области – гипотезу отвергают, если наблюдаемое значение критерия принадлежит области принятия гипотезы – гипотезу принимают. Для проверки гипотезы о закономерности распределения выборочной совокупности применяется критерий Пирсона (хи-квадрат), критические точки  которого находят по таблице.

Нулевую гипотезу следует принимать, если наблюдаемое значение критерия Пирсона меньше значения критической точки . Нулевую гипотезу следует отвергнуть, если наблюдаемое значение критерия Пирсона больше значения критической точки .

Для вычисления наблюдаемого значения критерия Пирсона  необходимо сравнить эмпирические  и теоретические  частоты каждого интервала статистического распределения выборки по формуле

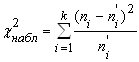, (30)

где k – количество интервалов.

Эмпирическая частота  равна количеству наблюдений в выборке, попавших в данный интервал. Теоретическая частота  вычисляется по формуле

, (31)

где Р_i – вероятность попадания случайной величины Х теоретического распределения в частичный интервал , n – объем выборки.

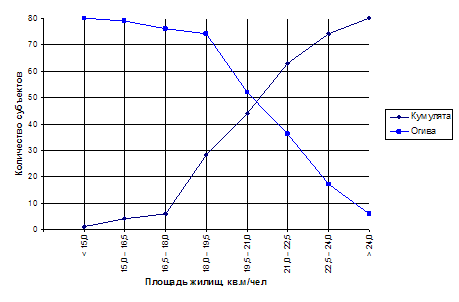
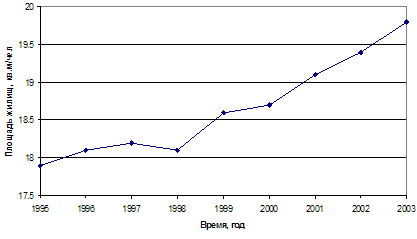
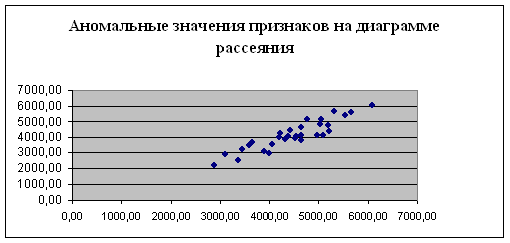
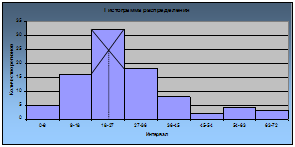
Выбор теоретического распределения определяется примерным совпадением вида гистограммы относительных частот статистического распределения с графиком плотности соответствующего распределения случайной величины Х (рис. 1, 2, 3). Результатом проведенного сравнительного анализа выступает выдвижение гипотезы о виде распределения выборочной совокупности и ее последующая проверка.

Для подтверждения выдвигаемой гипотезы сравниваются:

1) коэффициент асимметрии  статистического распределения с коэффициентами асимметрии  равномерного и нормального распределений ();

2) эксцесс  статистического распределения с эксцессами  равномерного () или нормального распределений ();

3) коэффициент вариации V статистического распределения с коэффициентами вариации показательного () распределения.

Характеристики выборочных совокупностей

Выборка	Характеристики
	Xmin	Xmax
1	5,1 ≈ 5	18,76 ≈ 20	6	2,5
2	0,18 ≈ 0	22,06 ≈ 25	5	5
3	0,03 ≈ 0	30,76 ≈ 35	7	5

Центральные эмпирические моменты выборок

Параметры	Выборка
	1	2	3
m2	16,48	19,62	48,58
m3	1,19	-3,79	513,41
m4	488,96	1053,94	11404,22

Параметры статистических распределений выборок

Параметры	Выборка
	1	2	3
	12,19	12,54	12,19
	4,06	4,43	6,97
	0,02	-0,04	1,5
	-1,20	-0,26	1,83
	0,33	0,35	0,57

- выборочная совокупность 1 имеет равномерное распределение с параметрами a=5,15 и b=19,22;

- выборочная совокупность 2 имеет нормальное распределение с параметрами a=12,54 и s=4,43;

- выборочная совокупность 3 имеет показательное распределение с параметром l=0,14.

Результаты сравнения коэффициентов асимметрии, эксцессов и коэффициентов вариации выборочных совокупностей не противоречат выдвинутым гипотезам:

- коэффициент асимметрии и коэффициент вариации V=0,33 выборочной совокупности 1 сравнимы с соответствующими параметрами равномерного распределения ();

- коэффициент асимметрии A^*_s=-0,04, эксцесс E^*_s=-0,26, выборочной совокупности 2 сравнимы с соответствующими параметрами нормального распределения ();

- коэффициент вариации V=0,57 выборочной совокупности 3 сравним с соответствующим параметром показательного распределения ().

Проверка гипотезы о равномерном распределении выборки 1

Нулевая гипотеза Н0: выборочная совокупность 1 имеет равномерное распределение с параметрами a=5,15 и b=19,22.

Число степеней свободы: r=3.

Уровень значимости α=0,05.

Критическая точка

Наблюдаемое значение критерия Пирсона

Критическая область :

Область принятия гипотезы :

Условие принятия Н0:

Условие непринятия Н0:

Результат проверки гипотезы: выборочная совокупность 1 имеет равномерное распределение с параметрами a=5,15 и b=19,22.

Проверка гипотезы о нормальном распределении выборки 2

Нулевая гипотеза Н0: выборочная совокупность 2 имеет нормальное распределение с параметрами a=12,54 и s=4,43.

Число степеней свободы: r=2.

Уровень значимости α=0,05

Критическая точка

Наблюдаемое значение критерия Пирсона

Критическая область:

Область принятия гипотезы :

Условие принятия Н0 :

Условие непринятия Н0:

Результат проверки гипотезы: выборочная совокупность 2 имеет нормальное распределение с параметрами a=12,54 и s=4,43.

Проверка гипотезы о показательном распределении выборки 3

Нулевая гипотеза Н0: Выборочная совокупность 3 имеет показательное распределение с параметром l=0,14.

Число степеней свободы: r=5

Уровень значимости α=0,05

Критическая точка

Наблюдаемое значение критерия Пирсона

Условие принятия Н0:

Результат проверки гипотезы: выборочная совокупность 3 имеет показательное распределение с параметром l=0,14.

Заключение

С помощью программы Excel был проведен статистический анализ 3-х выборочных совокупностей и было установлено, что:

-  выборочная совокупность 1 имеет равномерное распределение с параметрами a=5,15 и b=19,22;

-  выборочная совокупность 1 имеет нормальное распределение с параметрами a=12,54 и s=4,43;

-  выборочная совокупность 3 имеет показательное распределение с параметром l=0,14.

Список литературы

1.  Вентцель Е.С., Овчаров Л.А. Задачи и упражнения по теории вероятностей: учеб. пособие для вузов. 4-е изд., перераб. и доп. М.: Высш. шк., 2002. - 448 с.

2.  Гмурман В.Е. Теория вероятностей и математическая статистика: учеб. пособие для вузов. 9-е изд., стер. М.: Высш. шк., 2003. - 479 с.

3.  Гмурман В.Е. Руководство к решению задач по теории вероятностей и математической статистике: учеб. пособие для студентов вузов. Изд. 4-е, стер. – М.: Высш. шк., 1997. - 400 с.

4.  Горелова Г.В., Кацко И.А. Теория вероятностей и математическая статистика в примерах и задачах с применением Excel. Учебное пособие для вузов. Издание 2-е исправленное и дополненное. Ростов на Дону: Феникс, 2002. - 400 с.

5.  Елисеева Н.Н. и др. Теория статистики с основами теории вероятностей. - М.: ЮНИТИ, 2001. - 446 с.

6.  Куликова О.В., Тимофеева Г.А., Чуев Н.П. Исследование выборочных совокупностей с применением программы Excel – Екатеринбург.: УрГУПС, 2003. - 76 с.

7.  Макарова Н.В., Трофимец В.Я. Статистика в Excel: Учеб. пособие. – М.: Финансы и статистика, 2002. - 368 с.

8.  Гнеденко Б.В. Очерки по истории математики в России. – М.; Л.: Гос. изд-во техн.-теорет. лит., 1946. – 245 с.