Дискретизация масштаба и сдвига. Фреймы

4.2 Дискретизация масштаба и сдвига. Фреймы

В этом случае полагают дискретными величины a и b, т.е.  Частотное окно для анализа сохраняется прежним. Ширина временного окна

равна , а среднее значение изменяется дискретно пропорционально m -ой степени a₀ - масштабу вейвлета. Чем уже функция ψ, т.е. меньше величина, тем меньше (на ту же величину) шаг сдвига этой функции. Базисными функциями для дискретного вейвлет-преобразования будут функции, получаемые из 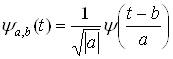,при  и  

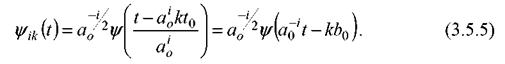
Коэффициенты разложения любой функции из L₂ могут быть получены как

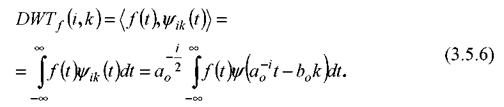
Выражение (3.5.6) является дискретным вейвлет-преобразованием функции . Чтобы обратное преобразование во временную область было справедливым, должно выполняться следующее условие:

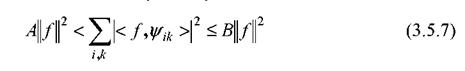
для всехесли константы A и B такие, чтоВ этом случае формула для восстановления функции f(t) по коэффициентам будет иметь вид

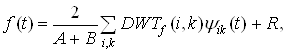(3.5.8)

где ошибку восстановления R можно оценить как  Разделив все члены неравенства (3.5.7) на, можно видеть, что константы A и B являются границами нормированной наэнергии – скалярного произведения. Они (эти константы) как бы "обрамляют" нормированную энергию коэффициентов Отсюда произошел термин фрейм (frame), которым называют множество функций  при которых условие (3.5.7) выполняется. Если A= B , то и множество  называют плотным фреймом. При этом выражение  вытекающее из (3.5.7), является обобщением теоремы Парсеваля на плотные фреймы. Для плотных фреймов из (3.5.8) получаем

Если A=B=1, то плотный фрейм становится ортогональным базисом. Заметим, что для вейвлетов, образованных материнским вейвлетом (3.3.6), хорошие результаты при восстановлении сигналов получаются при  так как . Для больших величин, например будет  т.е. восстановление приводит к большим искажениям.

4.3 Примеры вейвлетов для дискретного преобразования

Как было отмечено выше, функции вейвлет обладают свойством частотно-временной локализации, т.е. они ограничены как в частотной, так и во временной областях. Ниже рассмотрим два примера: первый – спектр вейвлетов в частотной области представляет собой идеальный полосовой фильтр, второй – сами функции вейвлет представляют собой прямоугольники. Все вейвлеты, с точки зрения частотно-временных свойств, занимают промежуточное положение между этими крайними случаями.

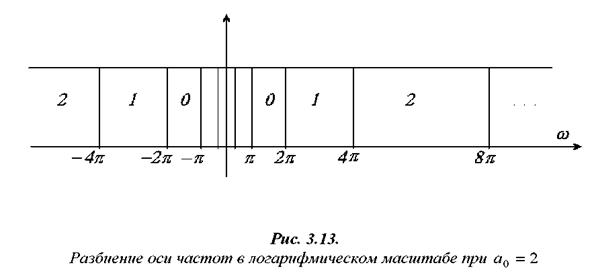
Sinc-базис. Разобьем ось частот на интервалы (поддиапазоны), как показано на рис. 3.13 при a₀ = 2. Такое разбиение называют логарифмическим, так как отношение верхней и нижней границ диапазонов постоянно и равно 2. Такое разбиение является еще и идеальным, так как оно реализуется идеальными полосовыми фильтрами. Подобная идеализация нужна для исследования свойств частотного разложения с помощью идеализированных вейвлетов, что позволит в дальнейшем перейти к более сложным разложениям. Любой сигнал  со спектром может занимать полосу частот, охватывающую несколько таких поддиапазонов.

Тогда и  т.е. сигнал представляет собой сумму некоторого числа элементарных сигналов. В рассматриваемом идеальном случае частотные каналы не перекрываются, поэтому имеет место ортогональность этих элементарных сигналов, т.е.

Выберем из всего множества сигналов такие, которые ограничены полосой частот 2^I, т.е. имеющие спектр . Рассмотрим периодическую функцию  такую, что: , т.е. полученную периодизацией F₁(ω) (рис. 3.14)

Тогда спектр функции: F_i (ω) при произвольном I можно представить в виде:

Где - функция окна такая, что:

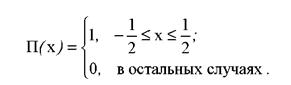
Посмотрим, как при этих условиях можно представить функцию f (t) во временной области. Для этого разложим периодическую функцию  с периодом , в ряд Фурье (см. ):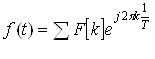

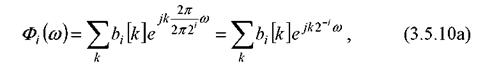
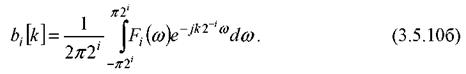
Где, подставляя (3.5.10а) в (3.5.9) и выполняя обратное преобразование Фурье, получим:

Вычислим первый интеграл. Переставляя операции суммирования и интегрирования и ограничивая пределы интегрирования с учетом функции окна, получим:

где вейвлет

(3.5.14)

и (см. рис. 3.16):

(3.5.15)

Выражение (3.5.13) является представлением функции f (t) в базисе вейвлет. В рассматриваемом частном случае идеальной полосовой фильтрации вейвлетом является функция (3.5.14), образованная из материнской функции  по (3.5.15) с учетом (3.5.12). Такой вейвлет называется sinc –вейвлетом по имени функции (3.5.12), которая его образует, а функция (3.5.12) получила название масштабной функции.

Множительпри  необходим для сохранения нормы  вне зависимости от величины масштаба, так как:

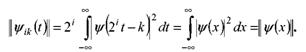
Покажем, что в рассматриваемом частном случае  т.е. определяется отсчетами функции при . Рассмотрим интеграл Фурье (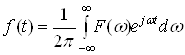) при дискретных значениях  функции, заданной на интервале Имеем, с учетом (3.5.10б):

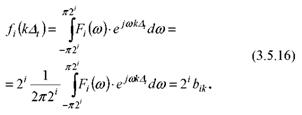
Последнее равенство справедливо при и вещественных

Следовательно,

Выполнив преобразование Фурье выражения (3.5.14), можно видеть, что спектр Фурье sinc -вейвлета представляет собой идеальный полосовой фильтр, в общем случае занимающий полосу частот от до

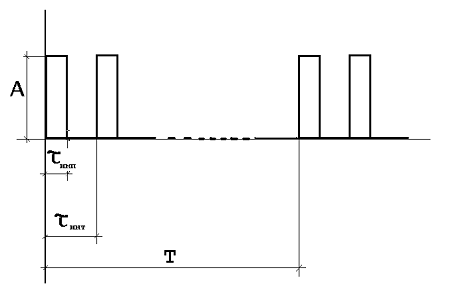
Вейвлет Хаара. Разобьем теперь временную ось на интервалы, как показано на рис. 3.17 и определим на единичном интервале функцию

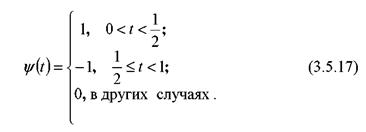
Эта функция является материнским вейвлетом, так как она удовлетворяет условию (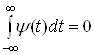). Система сдвигов таких функций  образует ортонормальный базис, так как их взаимная энергия равна нулю при  и равна единице при

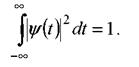
Преобразование Фурье (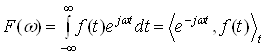) вейвлета Хаара имеет вид и показано на рис. 3.17б.

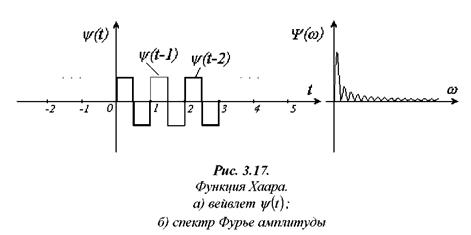
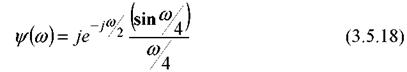
Функции Хаара, также как sinc -вейвлет, могут быть получены с помощью масштабной функции

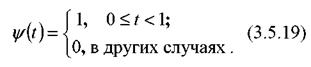
что иллюстрируется на рис. 3.18.

Из приведенных примеров следует ряд интересных выводов:

1. Представление вейвлет-функции в виде прямоугольников в любой из областей (частотной или временной) ведет к бесконечному расширению в противоположной области. Следовательно, для того, чтобы функции вейвлет были локализованы одновременно во временной и частотной областях, они должны убывать с ростом аргумента, по крайней мере, по закону обратной пропорциональности (см.(и )).

2.  Вейвлеты ψ(t), спектры Фурье которых представляют собой полосовые фильтры, могут быть выражены через масштабные функции (t), спектры Фурье которых представляют собой фильтры нижних частот (см. формулы (3.5.15) и (3.5.19)).

3.  Базисные функции для DWT могут быть получены из одной материнской функции путем ее масштабирования и сдвига (см. формулы (3.5.14) и (3.5.15)).

4.  Любой сигнал f(t) из L₂ может быть представлен своим вейвлет- разложением (3.5.13), если число компонентов f_i(t) таково, что они занимают полосу частот большую, чем полоса сигнала.

Литература

1. Новиков И.Я., Стечкин СБ. Основы теории всплесков // Успехи математических наук. 1998. V. 53. № 6. С.9-13.

2.Петухов А.П. Введение в теорию базисов всплесков. СПб.: Изд. СПбГТУ, 1999. 131 с.

3.Воробьев В.И., Грибунин В.Г. Теория и практика вейвлет-преобразования. СПб.: ВУС, 1999. 203 с.

4.  Астафьева Н.М. Вейвлет-анализ: основы теории и примеры применения// УФН . 1996. Т. 166, № 11. С. 1145-1170.

5.  Martin Vatterli, Jelena Kovačevic. Wavelets and Subband Coding. Prentice Hall, New Jersey, 1995.