Навигация
2. Свойства степенных рядов
Степенной ряд (1.2) представляет собой функцию ![]() , определенную в интервале сходимости
, определенную в интервале сходимости ![]() , т. е.
, т. е.
![]() .
.
Приведем несколько свойств функции ![]() .
.
Свойство 1. Функция ![]() является непрерывной на любом отрезке
является непрерывной на любом отрезке ![]() , принадлежащем интервалу сходимости
, принадлежащем интервалу сходимости ![]() .
.
Свойство 2. Функция ![]() дифференцируема на интервале
дифференцируема на интервале ![]() , и ее производная
, и ее производная ![]() может быть найдена почленным дифференцированием ряда (1.2), т. е.
может быть найдена почленным дифференцированием ряда (1.2), т. е.
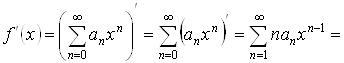
![]() ,
,
для всех ![]() .
.
Свойство 3. Неопределенный интеграл от функции ![]() для всех
для всех ![]() может быть получен почленным интегрированием ряда (1.2), т. е.
может быть получен почленным интегрированием ряда (1.2), т. е.
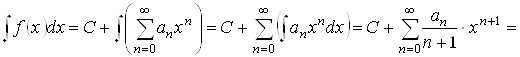
![]()
для всех ![]() .
.
Следует отметить, что при почленном дифференцировании и интегрировании степенного ряда его радиус сходимости R не меняется, однако его сходимость на концах интервала ![]() может измениться.
может измениться.
Приведенные свойства справедливы также и для степенных рядов (1.1).
Пример 2.1. Рассмотрим степенной ряд
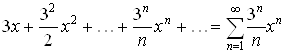 .
.
Область сходимости этого ряда, как показано в примере 1.1, есть промежуток 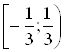 .
.
Почленно продифференцируем этот ряд:
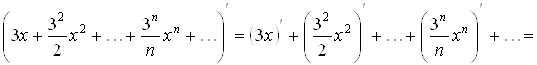
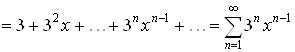 .(2.1)
.(2.1)
По свойству 2 интервал сходимости полученного степенного ряда (2.1) есть интервал 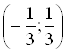 .
.
Исследуем поведение этого ряда на концах интервала сходимости, т. е. при ![]() и при
и при ![]() .
.
При ![]() степенной ряд (2.1) превращается в числовой ряд
степенной ряд (2.1) превращается в числовой ряд
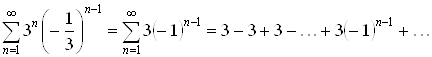 .
.
Этот числовой ряд расходится, так как не выполняется необходимый признак сходимости ![]() :
: ![]() , который не существует.
, который не существует.
При ![]() степенной ряд (2.1) превращается в числовой ряд
степенной ряд (2.1) превращается в числовой ряд
 ,
,
который также расходится, так как не выполняется необходимый признак сходимости.
Следовательно, область сходимости степенного ряда, полученного при почленном дифференцировании исходного степенного ряда, изменилась и совпадает с интервалом  .
.
3. Ряды Тейлора, Маклорена для функций
Пусть ![]() – дифференцируемая бесконечное число раз функция в окрестности точки
– дифференцируемая бесконечное число раз функция в окрестности точки ![]() , т. е. имеет производные любых порядков.
, т. е. имеет производные любых порядков.
Определение 3.1. Рядом Тейлора функции ![]() в точке
в точке ![]() называется степенной ряд
называется степенной ряд
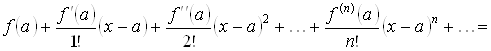
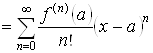 . (3.1)
. (3.1)
В частном случае при ![]() ряд (3.1) называется рядом Маклорена:
ряд (3.1) называется рядом Маклорена:
 . (3.2)
. (3.2)
Возникает вопрос: в каких случаях ряд Тейлора для дифференцированной бесконечное число раз функции ![]() в окрестности точки
в окрестности точки ![]() совпадает с функцией
совпадает с функцией ![]() ?
?
Возможны случаи, когда ряд Тейлора функции ![]() сходится, однако его сумма не равна
сходится, однако его сумма не равна ![]() .
.
Приведем достаточное условие сходимости ряда Тейлора функции ![]() к этой функции.
к этой функции.
Теорема 3.1:
если в интервале ![]() функция
функция ![]() имеет производные любого порядка и все они по абсолютной величине ограничены одним и тем же числом, т. е.
имеет производные любого порядка и все они по абсолютной величине ограничены одним и тем же числом, т. е. ![]() , то ряд Тейлора этой функции сходится к
, то ряд Тейлора этой функции сходится к ![]() для любого х из этого интервала
для любого х из этого интервала ![]() , т. е. имеет место равенство
, т. е. имеет место равенство
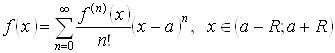 .
.
Для выяснения выполнения этого равенства на концах интервала сходимости требуются отдельные исследования.
Следует отметить, что если функция разлагается в степенной ряд, то этот ряд является рядом Тейлора (Маклорена) этой функции, причем это разложение единственно.
Похожие работы
... процессов. М.: Наука, 1969, Гл.1. §5. Болтянский В.Г. Математические методы оптимального управления. М.: Наука, 1969, Гл.1. §3. Понтрягин Л.С. Обыкновенные дифференциальные уравнения. М.: Наука, 1974, Гл.2. §16. Арнольд В. И. Обыкновенные дифференциальные уравнения. М.: Наука, 1975, ГЛ.2. §12. С.73-78, 84-85. program coefficients; type mas=array[1..100] of real;beg=array[1..6] of real; var ...
... р2; В первом случае l -комплексные; Ѕ l 2 Ѕ =q; (20) если q<1; устойчивость q>1 - неустойчивость. Случай второй - l - действительные: ; (21) устойчивость соответствует p и q нетрудно получить в виде рядов по степени m из формул (19) (12). (22) Если принять во внимание (15) (22a)(23) Мы видим, что при достаточно малом m и w № n; n ' Z вопрос об устойчивости решается величиной q и ...
... , то отрицательны. Т.Лейбница: Если члены знакочередующегося ряда убывают по абсолютной величине U1>U2>U3… и предел его общего члена при n®¥ равен 0 (Lim n®¥ Un=0), то ряд сходится, а его сумма не превосходит первого члена: U1³S. Д: Рассмотрим последовательность частичных сумм четного числа членов при n=2m: S2m=(U1-U2)+(U3-U4)+…+(U2m-1-U2m). Эта последовательность ...
... до бесконечности вместе с n. 1.2 Истоки проблемы Различные факты из области математического анализа, как, например, расходимость, произведения двух сходящихся рядов, естественно выдвинули вышеупомянутый вопрос: “О возможности суммирования расходящихся рядов, в некоем новом смысле”. Нужно сказать, что до создания Коши строгой теории пределов (и связанной с нею теории рядов) расходящиеся ...
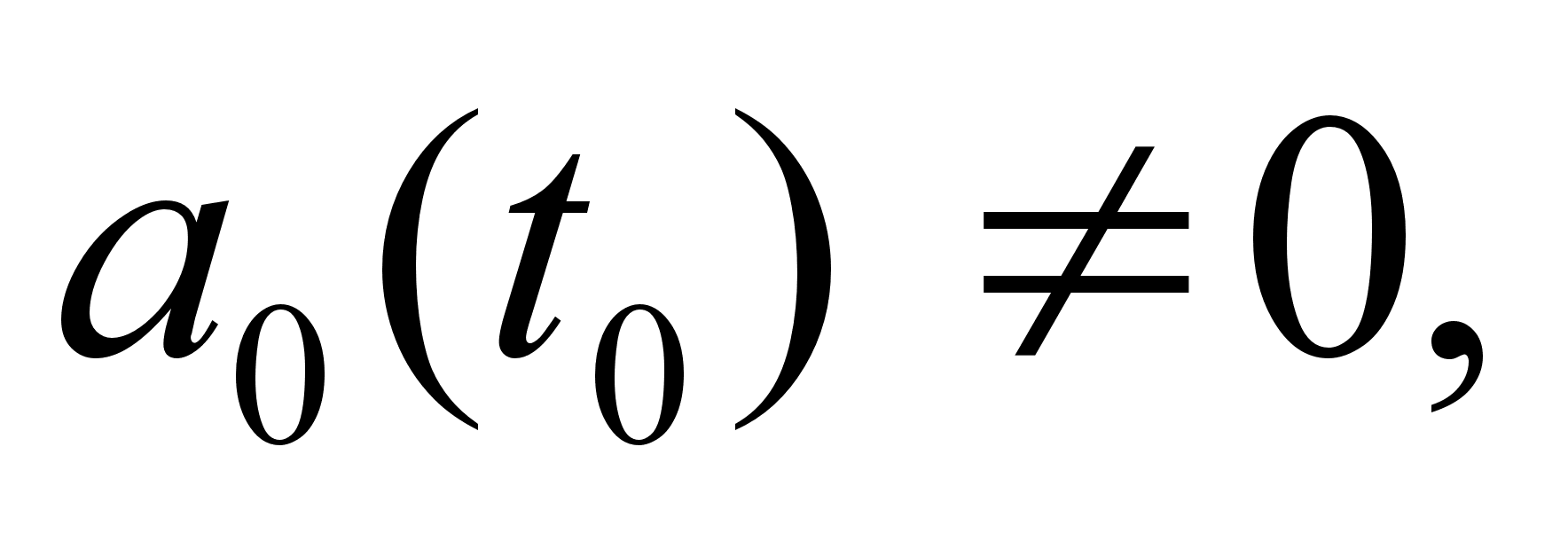
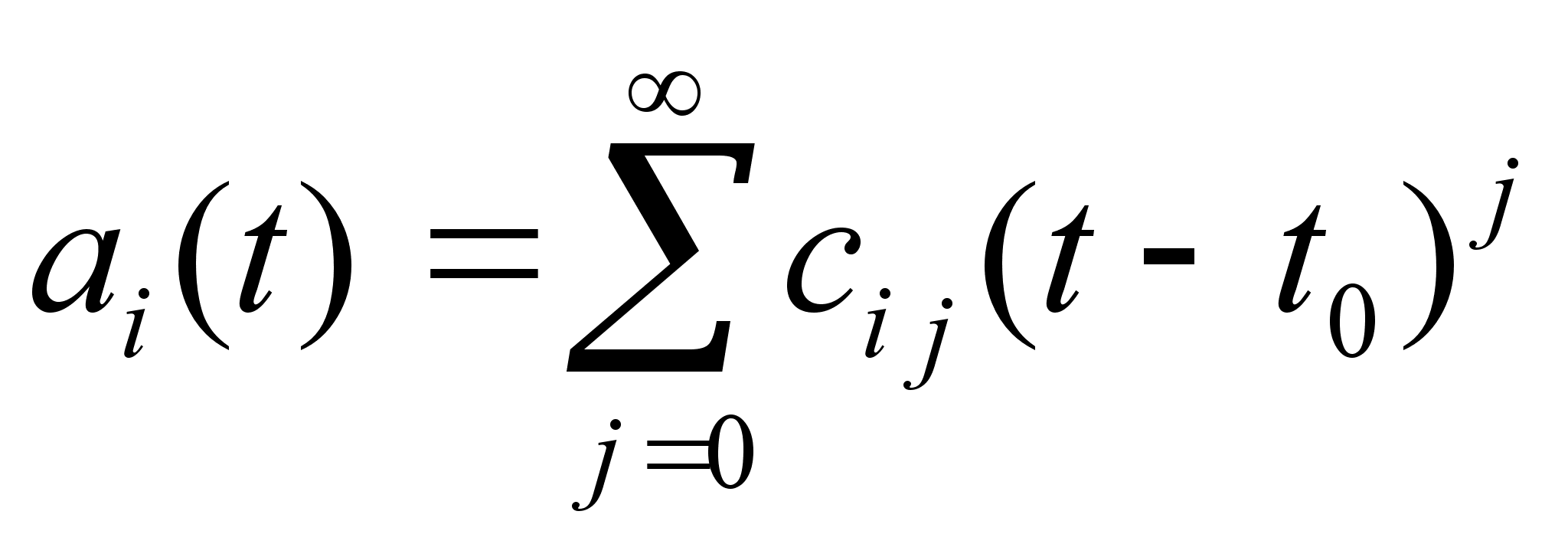

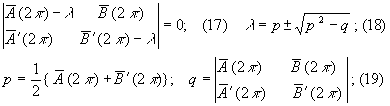

0 комментариев