Навигация
Разложение некоторых элементарных функций в ряд Маклорена
4. Разложение некоторых элементарных функций в ряд Маклорена
1. ![]() . Для этой функции
. Для этой функции ![]() ,
, ![]() .
.
По формуле (3.2) составим ряд Маклорена данной функции:
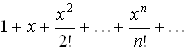 . (3.3)
. (3.3)
Найдем радиус сходимости ряда (3.3) по формуле (1.3):
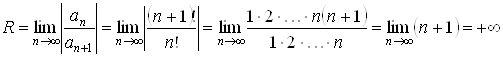 .
.
Следовательно, ряд (3.3) сходится при любом значении ![]() .
.
Все производные функции ![]() на любом отрезке
на любом отрезке ![]() ограничены, т. е.
ограничены, т. е.
![]() .
.
Поэтому, согласно теореме 3.1, имеет место разложение
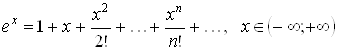 . (3.4)
. (3.4)
2. ![]() . Для этой функции
. Для этой функции 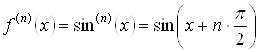 ,
, 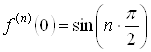 ,
, ![]() .
.
Отсюда следует, что при ![]() производные четного порядка равны нулю, а производные нечетного порядка чередуют знак с плюса на минус.
производные четного порядка равны нулю, а производные нечетного порядка чередуют знак с плюса на минус.
По формуле (3.2) составим ряд Маклорена:
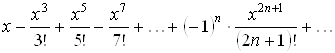 .
.
При любом фиксированном значении этот ряд сходится как знакочередующийся по признаку Лейбница. При этом
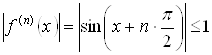
![]()
![]() .
.
Поэтому, согласно теореме 3.1, имеет место разложение
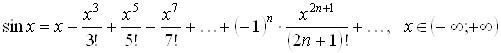 . (3.5)
. (3.5)
3. ![]() . Воспользуемся разложением (3.5) в ряд Маклорена функции
. Воспользуемся разложением (3.5) в ряд Маклорена функции ![]() и свойством 2 о дифференцировании степенного ряда. Имеем
и свойством 2 о дифференцировании степенного ряда. Имеем
|
| (3.6) |
Поскольку при почленном дифференцировании интервал сходимости степенного ряда не изменяется, то разложение (3.6) имеет место при любом ![]() .
.
Приведем без доказательства разложения других элементарных функций в ряды Маклорена.
4. ![]()
![]() – биномиальный ряд (
– биномиальный ряд (![]() – любое действительное число).
– любое действительное число).
Если ![]() – положительное целое число, то получаем бином Ньютона:
– положительное целое число, то получаем бином Ньютона:
![]() .
.
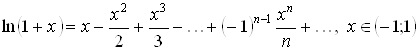 – логарифмический ряд.
– логарифмический ряд.
![]() .
.
5. Приложения степенных рядов
Степенные ряды находят применение в таких задачах, как приближенное вычисление функций с заданной степенью точности, определенных интегралов, решение дифференциальных уравнений и др.
Приближенное значение функции вычисляют, заменяя ряд Маклорена этой функции конечным числом его членов.
Приведем приближенные формулы для вычисления некоторых наиболее часто встречающихся функций при достаточно малых значениях х:
![]() ;
; ![]() ;
; ![]() ;
; ![]() ;
;
![]() ;
; ![]() .
.
Литература
1. Высшая математика: Общий курс: Учебник – 2-е изд., перераб. / А.И. Яблонский, А.В. Кузнецов, Е.И. Шилкина и др.; Под общ. ред. С.А. Самаля. – Мн.: Выш. шк., 2000.– 351 с.
2. Марков Л.Н., Размыслович Г.П. Высшая математика. Ч. 2. Основы математического анализа и элементы дифференциальных уравнений. – Мн.: Амалфея, 2003. – 352 с. ![]()
Похожие работы
... процессов. М.: Наука, 1969, Гл.1. §5. Болтянский В.Г. Математические методы оптимального управления. М.: Наука, 1969, Гл.1. §3. Понтрягин Л.С. Обыкновенные дифференциальные уравнения. М.: Наука, 1974, Гл.2. §16. Арнольд В. И. Обыкновенные дифференциальные уравнения. М.: Наука, 1975, ГЛ.2. §12. С.73-78, 84-85. program coefficients; type mas=array[1..100] of real;beg=array[1..6] of real; var ...
... р2; В первом случае l -комплексные; Ѕ l 2 Ѕ =q; (20) если q<1; устойчивость q>1 - неустойчивость. Случай второй - l - действительные: ; (21) устойчивость соответствует p и q нетрудно получить в виде рядов по степени m из формул (19) (12). (22) Если принять во внимание (15) (22a)(23) Мы видим, что при достаточно малом m и w № n; n ' Z вопрос об устойчивости решается величиной q и ...
... , то отрицательны. Т.Лейбница: Если члены знакочередующегося ряда убывают по абсолютной величине U1>U2>U3… и предел его общего члена при n®¥ равен 0 (Lim n®¥ Un=0), то ряд сходится, а его сумма не превосходит первого члена: U1³S. Д: Рассмотрим последовательность частичных сумм четного числа членов при n=2m: S2m=(U1-U2)+(U3-U4)+…+(U2m-1-U2m). Эта последовательность ...
... до бесконечности вместе с n. 1.2 Истоки проблемы Различные факты из области математического анализа, как, например, расходимость, произведения двух сходящихся рядов, естественно выдвинули вышеупомянутый вопрос: “О возможности суммирования расходящихся рядов, в некоем новом смысле”. Нужно сказать, что до создания Коши строгой теории пределов (и связанной с нею теории рядов) расходящиеся ...
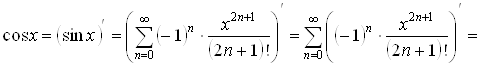
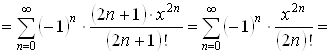
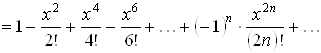 .
.


0 комментариев