Составляют функцию Лагранжа

2. Составляют функцию Лагранжа

гдеR — множитель Лагранжа. Очевидно, что на множестве L второе слагаемое обращается в нуль вследствие выполнения условия F(x, у) = 0. Таким образом, на L выполненои поэтому задача в случае функции двух переменных, сводится к поиску экстремума функции одной переменной х.

Формально процедура решения такова. Приравниваем к нулю все частные производные функции Лагранжа:

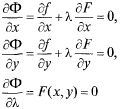
и отсюда находим решение

Пусть— любое из решений этой системы.

Подставляя внайденный из

уравнения связи дифференциали обозначая

(в опорном конспекте № 12записано в виде определителя), получаемТогда, еслиимеет в т.

условный максимум, если> 0 — то условный минимум.

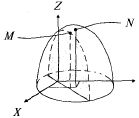
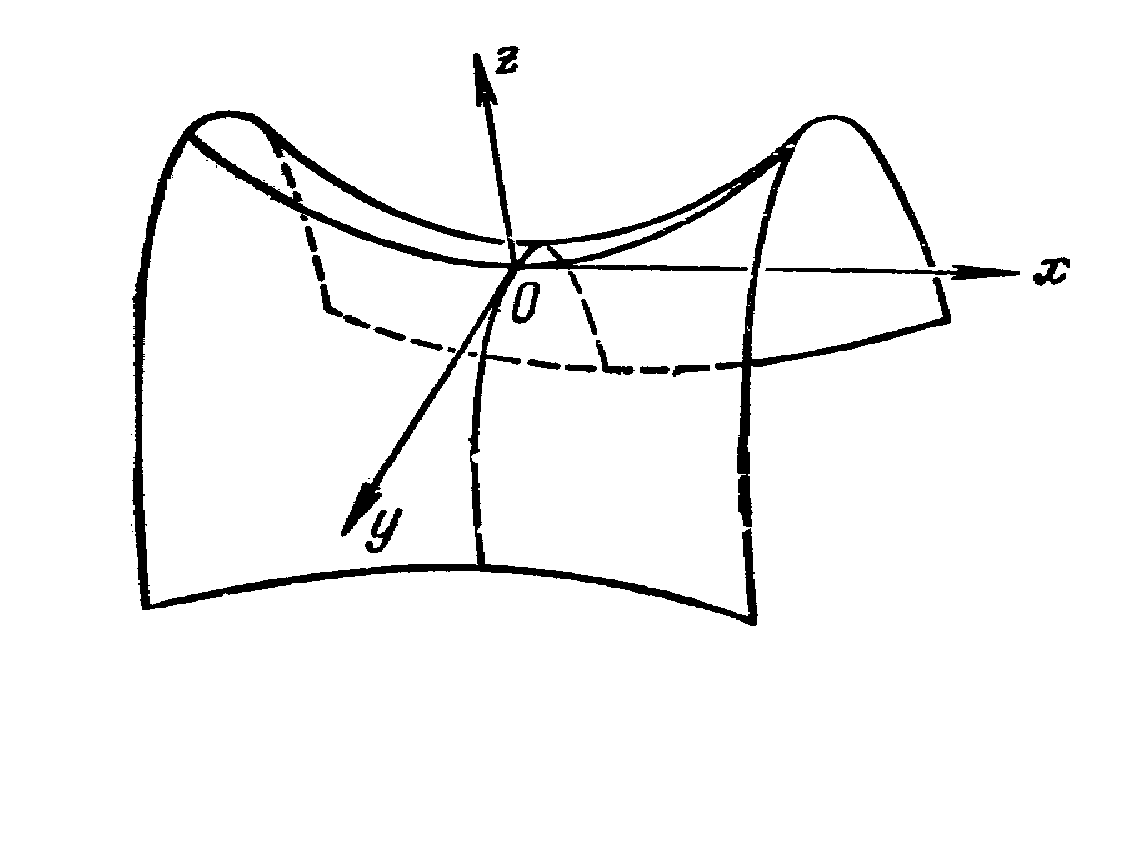
Пример: Найти точки экстремума функцииесли уравнение связи у - х = 0. Рассмотрим оба способа решения. 1. Из аналитической геометрии известно, что любое уравнение 2-го порядка определяет в пространстве поверхность второго порядка . Выделим в заданном уравнении полные квадраты х и у:— уравнение параболоида вращения с вершиной в т. N(1, 2, 9) (рис. 12.3); у = х — уравнение плоскости. Подставляя уравнение связи в исходную функцию, получаем

 

Исследуем на экстремум:

— максимум в т.М(1,5; 1,5).

Функцияимеет условный экстремум

= 4-2 · 2,25 + 6 · 1,5 = 13 - 4,5 = 8,5. 2. Составим

линейная система уравнений.

Используя метод Крамера, получим:и

— т. условного максимума

Для функциипри наличии m уравнений связи функция Лагранжа будет иметь вид

Необходимые условия условного экстремума выражаются системой (n + m) уравнений:

 

Правило исключения интервалов

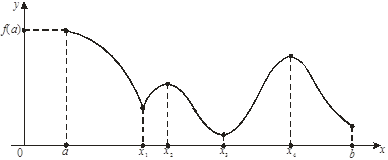
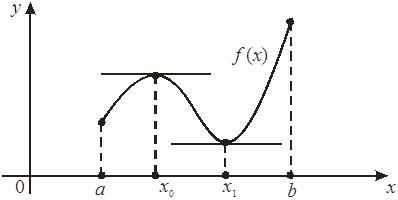
Пусть функция f унимодальна на интервале a£x£b, а ее минимум достигается в точке x*.

Рассмотрим точки x₁ и x₂, расположенные в интервале таким образом, что a<x₁<x₂<b. Сравнивая значения функции в точках x₁ и x₂, можно сделать следующие выводы:

Если f(x₁)>f(x₂), то точка минимума f(x) не лежит в интервале (a,x₁), т.е. x*Î(x₁,b)

2. Если f(x₁)<f(x₂), то точка минимума не лежит в интервале (x₂,b), т.е. x*Î(a,x₂)

3. Если f(x₁)=f(x₂), то можно исключить оба крайних интервала (a,x₁) и (x₂,b), при этом x*Î(x₁,x₂).

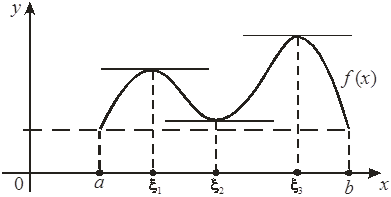
Согласно правилу исключения интервалов можно реализовать процедуру поиска, позволяющую найти точку оптимума путем последовательного исключения частей исходного ограниченного интервала.

Поиск завершается, когда оставшийся интервал уменьшается до достаточно малых размеров.

Достоинства этих методов:

устраняется необходимость полного перебора всех допустимых точек.

методы основаны лишь на вычислении значений функции.

(при этом не требуется, чтобы исследуемые функции были дифференцируемы).

Метод золотого сечения

В методе же золотого сечения мы будем выбирать расположение точек х₁ и х₂, рассекающих интервал, таким образом, чтобы на каждом шаге уменьшения интервала одна из этих точек совпадала с одной из аналогичных точек предыдущего шага, т.е. на каждом шагу уменьшения интервала фактически вводится только одна новая точка, для которой требуется произвести только одно вычисление значения целевой функции.

Такое рассечение интервала новой точкой может быть точно рассчитано. Забегая вперед, запишу эту пропорцию:

Точки х₁ и х₂ расположены симметрично относительно середины интервала (a, b).

b-x₁ x₂-a -1+

= = » 0.618

b-a b-a 2 .

Такое рассечение интервала и получило название золотого сечения.

Введем обозначения:

D¹ = b-a – исходный интервал.

D² – интервал, полученный после уменьшения интервала D¹ отбрасыванием его левого или правого подинтервала.

D^К+1 – интервал, полученный после уменьшения интервала D^К.

Рассмотрим теперь метод золотого сечения формально. Золотым сечением отрезка называется деление отрезка на две неравные части так, чтобы отношение всего отрезка к большей части равнялось отношению большей части к меньшей.

Золотое сечение отрезка [a, b] производится двумя симметрично расположенными точками (х₁ и х₂).

Т.е. (b-a)/(b-x₁)=(b-x₁)/(x₁-a)=g и (b-a)/(x₂-a)=(x₂-a)/(b-x₂)=g.

Можно показать, что g = (1+Ö5)/2»1.618.

Примечательно то, что точка х₁ в свою очередь производит золотое сечение отрезка [a, x₂], т.е. (x₂-a)/(x₁-a) = (x₁-a)/(x₂-x₁) = g.

Аналогично, точка х₂ производит золотое сечение отрезка [x₁, b].

Итак, метод золотого сечения состоит в том, что длины последовательных интервалов берутся в фиксированном отношении:

D¹/D² = D²/D³  = … =g.

Из соотношений D^К/D^K+1 = D^K+1/D^K+2 = g и D^K = D^K+1 + D^K+2

Получаем: D^K/D^K+1 = (D^K+1+D^K+2)/D^K+1=1+D^K+2/D^K+1

g = 1 + 1/g или g² - g -1 = 0.

Корнем этого уравнения является золотое сечение.

g=(Ö5+1)/2 » 1.618  t = 1/g = (Ö5-1)/2 » 0.618.

Можно записать формулы для точек х₁ и х₂, производящих золотое сечение на интервале [a, b]:

x₁ = a+(1-t)(b-a) x₂ = a+t(b-a)

Алгоритм метода золотого сечения.

Ввести a, b, e-точность вычисления, t=(Ö5-1)/2

Вычислить:

x₁ =b – (b-a)t; x₂ =a + (b-a)t

Вычислить: y₁ = f(x₁); y₂ = f(x₂)

если y₁£y₂, то для дальнейшего деления оставляют интервал [a, x₂]

и выполняют следующее:

b: = x₂; x₂: = x₁; y₂: = y₁; x₁ := b-(b-a)t y₁ := f(x₁)

в противном случае (если y₁ > y₂), для дальнейшего деления оставляют интервал [x₁, b] и выполняют следующее:

a := x₁; x₁ := x₂; y₁ := y₂; x₂ := a+(b-a)t; y₂ :=f(x₂);

Сравнение длины интервала неопределенности с заданной точностью e:

Если (b-a)£e, то положить x* := (b-a)/2 (точка минимума), иначе (если (b-a)<e) перейти к п.4.

Максимум и минимум функции нескольких переменных

Напомним, что под окрестностью точки плоскости понимается внутренность любого прямоугольника, окружающего эту точку, исключая саму точку (проколотая окрестность).

В пространстве это будет произвольный параллелепипед, содержащий эту точку за вычетом самой точки.

Определение 15.1. Максимумом (строгим) функции f (x, y) называется такое значение f(x₁, y₁) этой функции, которое больше всех ее значений f(x, y), принимаемых данной функцией в точках некоторой окрестности точки О(х₁, у₁). (Окрестность может быть весьма малой по своим линейным размерам).

Определение 15.2. Минимумом (строгим) функции f (x, y) называется такое значение f (x₂,y₂), которое меньше всех ее значений f (x,y), принимаемых данной функцией в точках некоторой окрестности О (х₂, у₂).

Максимум или минимум функции f (x, y) называется экстремумом этой функции. Точка, в которой достигается экстремум, называется точкой экстремума (точка минимума, точка максимума).

Аналогично определяется экстремум функции f (x, y, z) и т.д.

Теорема 15.1. (Необходимый признак экстремума функции нескольких переменных). В точке экстремума функции нескольких переменных каждая ее частная производная первого порядка либо равна нулю, либо не существует.

Доказательство. Пусть u = f (x, y) и f (x_o, y_o) - ее максимум (для минимума рассуждения аналогичны). Зафиксируем одну из переменных, например, у, полагая у = у_о, тогда получим функцию одной переменной U₁ = f (x, y_o), которая, очевидно, будет иметь максимум при х = х_о. Отсюда, на основании теории экстремума одной переменной, получаем, что или  не существует.

Пусть теперь у=у_о, а х_о- фиксируем, тогда или не существует.

Следствие В точке экстремума М_о (х_о, у_о) дифференцируемой функции f (x, y) выполнены равенства  

Для U = f(x,y, z) в точке М_о (х_{о ,}у_о, z_о) будет выполнено условие .

Замечание. Точку, в которой частные производные первого порядка либо не существуют, либо равны нулю, называют критической.

Т.е. экстремумы функции нескольких переменных могут достигаться лишь в критических точках.

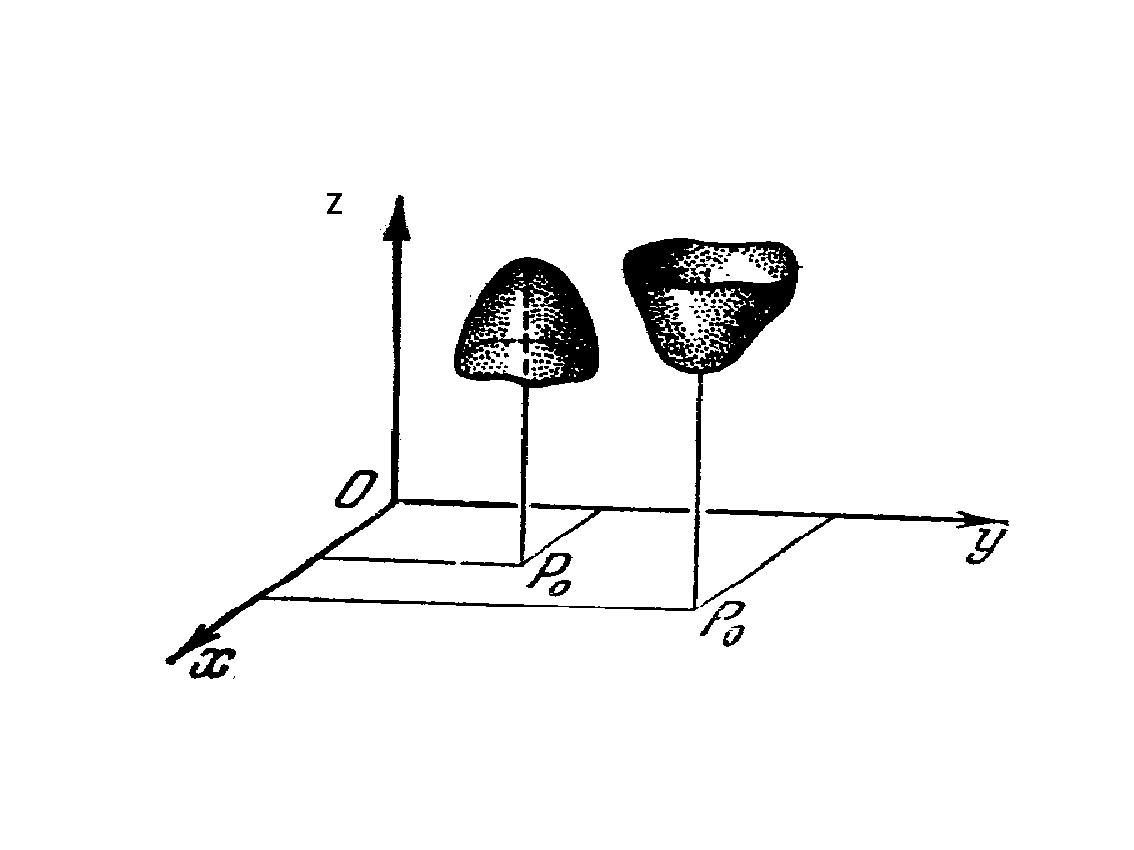
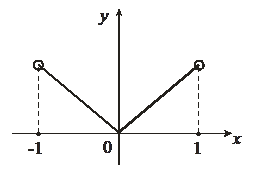
Пример 15.1. Покажем, что указанные выше условия не являются достаточными. Пусть z = f(x, y) = x × y тогда имеем

Следовательно,  Однако точка 0(0,0) не является точкой экстремума, т.к. в любой окрестности точки 0 (о,о) имеются точки

A (e,e) и B(- e, e) " e > 0 :

f(A) = e² > 0 = f(0) и f(B) = - e² < f(0).

 

Абсолютный экстремум

 

Определение 15.3. Наименьшее или наибольшее значение функции в данной области называется абсолютным экстремумом функции. (Соответственно, абсолютный минимум, абсолютный максимум).

Теорема 15.2. (Вайерштрасс) Функция, непрерывная в ограниченной и замкнутой области, достигает в этой области своего наименьшего и своего наибольшего значения. (Без доказательства)

Теорема 15.3. Абсолютный экстремум функции в данной области достигается либо в критической точке функции, принадлежащей этой области, либо в граничной точке области. (Без доказательства)

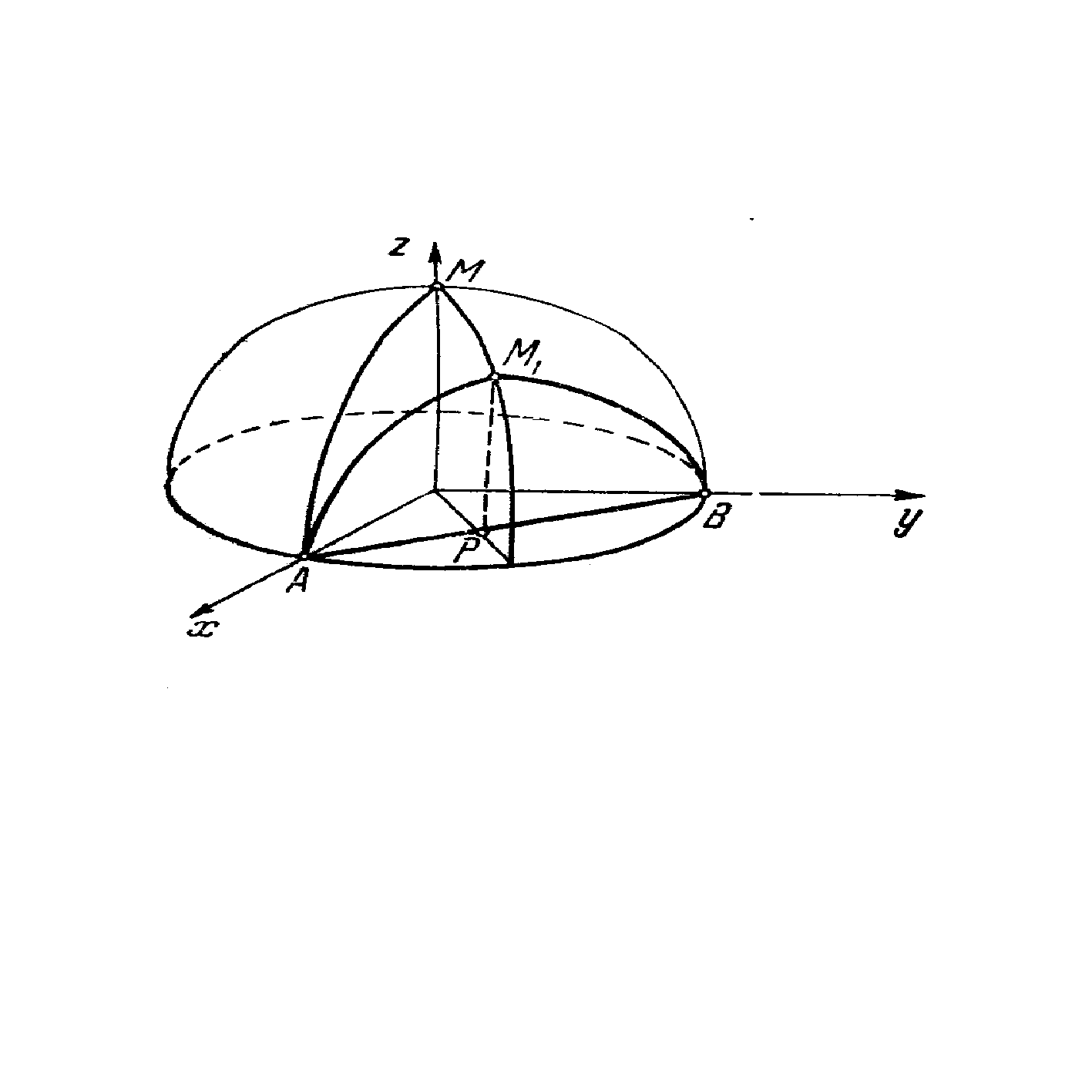
Пример 15.2. Для функции z = x × y найти абсолютный экстремум в треугольной области S с вершинами О(0,0), А(1,0), В(0,2).

Определим

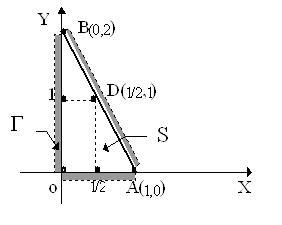
Критическая точка O(0,0) Î S. На участке ОА имеем у = 0 (0 £ х £ 1) и тогда z = 0.

Аналогично ОВ: х = 0 (0 £ у £ 2) Þ z = 0.

Наконец, отрезок АВ имеет уравнение или у = 2 - 2х (0 £ х £ 1).

Отсюда

z = x × y = 2x - 2x² .

Имеем , т.е. при  и т.к. , то в точке  функция Z достигает своего наибольшего значения  на отрезке АВ.

 Итак, наименьшее значение z в S есть m=0 и оно реализуется в точках отрезков ОВ и ОА, составляющих часть границы Г.

 

достигает в точке

Заключение

В работе приведены и численные методы нахождения экстремума. Необходимость в них возникает, когда система из частных производных не имеет аналитического решения или содержит сложную нелинейность. Аналитически решается лишь малая часть задач оптимизации, поэтому рассматриваются и некоторые численные алгоритмы. Численные алгоритмы запрограммированы, как правило, в математических компьютерных пакетах, которые обеспечивают высокую точность и скорость нахождения экстремума, но, к сожалению, не всегда находят глобальный экстремум. Среди таких пакетов следует отметить математические программы Maple, MatLab, Mathematica. Но это не означает, что для нахождения экстремумов следует пользоваться ими, не имея понятия о математических алгоритмах.

В работе в виду ограниченного объема не рассматривались задачи оптимизации функций с ограничениями, и задачи многокритериальной оптимизации. Тем не менее, они составляют важный класс задач поиска экстремума, которые часто появляются в научной и практической деятельности.

 

Литература

1.  Акулич И.Л. Математическое программирование в примерах и задачах. - М.: Высшая школа, 1986.

2.  Алексеев В.М., Галеев Э.М., Тихомиров В.М. Сборник задач по оптимизации. - М.: Наука, 1984.

3.  Банди Б. Методы оптимизации. Вводный курс. - М.: Радио и связь, 1988.

4.  Васильев Ф.П. Численные методы решения экстремальных задач. - М.: Наука, 1980.

5.  Гилл Ф., Мюррей У., Райт М. Практическая оптимизация. - М.: Мир, 1985.

6.  Евтушенко Ю.Г. Методы решения экстремальных задач и их применение в системах оптимизации. - М.: Наука, 1982.

7.  Карманов В.Г. Математическое программирование. - М.: Наука, 1975.

8.  Лесин В.В., Лисовец Ю.П. Основы методов оптимизации. - М.: Изд-во МАИ, 1995.

9.  Летова Т.А., Пантелеев А.В. Экстремум функций в примерах и задачах. M.: Изд-во МАИ, 1998.

10.  Пшеничный Б.И., Данилин Ю.М. Численные методы в экстремальных задачах. - М.: Наука, 1975.

11.  Федоров В.В. Численные методы максимина. - М.: Наука, 1979.