Навигация
Практическое применение геометрии Лобачевского
24411
знаков
0
таблиц
11
изображений
5. Практическое применение геометрии Лобачевского.
1) Теорема Пифагора.
Теорема. Для всякого прямоугольного треугольника плоскости Лобачевского выполняется равенство ch c = ch a ·ch b, где a, b - длины катетов, c - длина гипотенузы этого треугольника, а ch x=
(гиперболический косинус).
Доказательство. Воспользуемся моделью Пуанкаре плоскости Лобачевского на евклидовой полуплоскости. Будем считать (см. рисунок ниже), что вершинам A, B, C данного прямоугольного треугольника соответствуют комплексные числа 
где 
так как этого всегда можно добиться с помощью некоторого неевклидова движения.
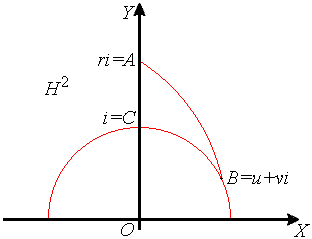
Используя формулу
для вычисления неевклидова расстояния между точками z и w в H2, получаем, что
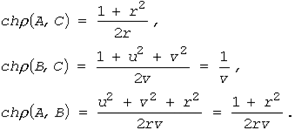
Почленное перемножение двух первых соотношений и приводит, как показывает третье соотношение, к завершению доказательства теоремы.
2) Замечание к теореме Пифагора Н.И.Лобачевским было замечено, что созданная им неевклидова геометрия в бесконечно малом, то есть в первом приближении, совпадает с геометрией евклидовой плоскости. Проиллюстрируем это на примере теоремы Пифагора. Используя разложение гиперболического косинуса в ряд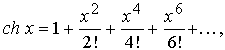
получим для теоремы Пифагора соотношение
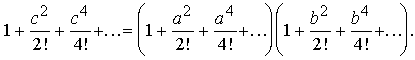
Исключая теперь члены низшего порядка, приходим к теореме Пифагора евклидовой геометрии:
Подробный вывод формулы площади треугольника на плоскости Лобачевского я приводить не буду ввиду его сложности (в нем используется формулы, доказываемые лишь в курсе дифференциальной геометрии).
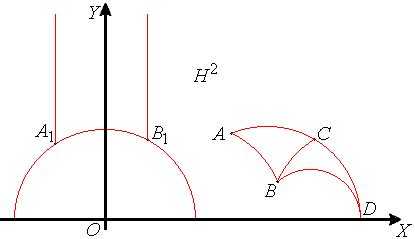Если ABC - треугольник в модели Пуанкаре, меры углов A, B и C - α, β и γ соответственно, 
- мера угла B в треугольнике ABD, а 
и 
мера углов B и C в треугольнике BCD. Тогда 
Вследствие этого можно сформулировать теорему
Теорема.Для площади треугольника ABC с углами
справедлива формула
Следствие1.Площадь треугольника плоскости Лобачевского ограничена.
Следствие 2.Если дан выпуклый многоугольник 
с внутренними углами 
то
Теорема. Площадь круга с радиусом r равна 
а длина окружности, ограничивающей этот круг, равна 
, где 
. Длина неевклидовой окружности не пропорциональна радиусу, как в случае евклидовой геометрии, а растет быстрее. Также площадь неевклидова круга больше площади круга евклидовой плоскости, имеющего тот же радиус.
6. Вывод:
Открытие неевклидовой геометрии, начало которому положил Лобачевский, не только сыграло огромную роль в развитии новых идей и методов в математике естествознании, но имеет и философское значение. Господствовавшее до Лобачевского мнение о незыблемости геометрии Евклида в значительной мере основывалось на учении известного немецкого философа И. Канта (1724-1804), родоначальника немецкого классического идеализма. Кант утверждал, что человек упорядочивает явления реального мира согласно априорным представлениям, а геометрические представления и идеи якобы априорны (латинское слово aprior означает – изначально, заранее), то есть, не отражают явлений действительного мира, не зависят от практики, от опыта, а являются врожденными человеческому миру, раз и навсегда зафиксированными, свойственными человеческому разуму, его духу. Поэтому, Кант считал, что Евклидова геометрия непоколебима, неизменна, и является вечной истиной. Еще до Канта геометрия Евклида считалась незыблемой, как единственно возможное учение о реальном пространстве.
Открытие неевклидовой геометрии доказало, что нельзя абсолютировать представления о пространстве, что «употребительная» (как назвал Лобачевский геометрию Евклида) геометрия не является единственно возможной, однако это не подорвало незыблемость геометрии Евклида. Итак, в основе геометрии Евклида лежат не априорные, врожденные уму понятия и аксиомы, а такие понятия, которые связаны с деятельностью человека, с человеческой практикой. Только практика может решить вопрос о том, какая геометрия вернее излагает свойства физического пространства. Открытие неевклидовой геометрии дало решающий толчок грандиозному развитию науки, способствовало и поныне способствует более глубокому пониманию окружающего нас материального мира.
Список источников:
1. Математика XIX века, «Наука», М., 1981
2. “Квант” №11,№12 Академик АН СССР А.Д. Александров, Интернет-издания.
3. Юшкевич А.П., История математики в России, «Наука», М., 1968
4. Ефимов Н.В., Высшая геометрия, «Наука», М.,1971.
5. Неевклидовы пространства и новые проблемы физики, «Белка», М., 1993
6. Клайн М., Математика. Утрата определенности, «Мир», М., 1984
7. Г.И. Глейзер. История математики в школе IX – X классы. Пособие для учителей. Москва, «Просвещение» 1983г.
8. Даан Дальмедино А., Пейффер И. Пути и лабиринты. Очерки по истории математики. Перевод с французского. М: Мир.1986г.
9. Б.Л. Лаптев. Н.И. Лобачевский и его геометрия. Пособие для учащихся. М. «Просвещение», 1970г.
10. И.М. Яглам. Принцип относительности Галилея и неевклидова геометрия. Серия «Библиотека математического кружка» М: 1963г.
11. http://www.bankreferatov.ru
12. http://www.refportal.ru
13. http://www.edu.ru
14. http://www.
15. http://www.themesoch.narod.ru/t_s
16. http://www.referat.online.ru
17. http://www.pautina.net
Похожие работы
... представить другие геометрии Кант счел достаточным основанием, чтобы утверждать, что другие геометрии не могут существовать. Появление неевклидовой геометрии Но многовековые попытки доказательства пятого постулата Евклида привели в конце концов к появлению новой геометрии, отличающейся от евклидовой тем, что в ней V постулат не выполняется. Эта геометрия теперь называется неевклидовой, а в ...
... , т. е. такие пары точек считаются за одну точку. Из этого определения следует, что при возрастании n число типов неевклидовых пространств также растет. Неевклидовы геометрии являются геометриями простейших римановых пространств определенной и неопределенной метрики, составляющих так называемый класс пространств постоянной ненулевой кривизны. Каждое из таких n-мерных пространств допускает ...
... целых три доказательства V постулата, ошибочность которых быстро показали его современники. Последнее «доказательство» он опубликовал в 1823 году, за три года до первого доклада Лобачевского о новой геометрии. Открытие неевклидовой геометрии В первой половине XIX века по пути, проложенному Саккери, пошли сразу три математика: К.Ф. Гаусс, Н.И. Лобачевский и Я. Бойяи. Но цель у них была уже иная ...
... живой. Пусть новых линий не начертят руки, Он здесь стоит, взнесенный высоко, Как утверждение бессмертья своего, Как вечный символ торжества науки. Другие авторы. Идея неевклидовой геометрии пришла в голову не только Лобачевскому – просто ему относительно повезло. Одним из «конкурентов» был Гаусс – великий затворник, отказавшийся от услуг почты, чтобы никто не смог обвинить его в плагиате. ...
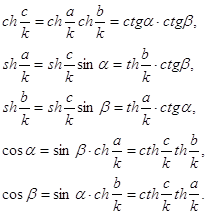
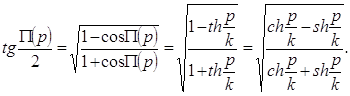
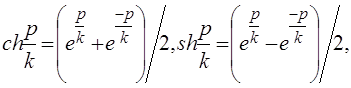
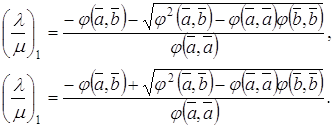
0 комментариев