Навигация
Министерство образования и науки Российской Федерации
Федеральное агентство по образованию
Государственное образовательное учреждение высшего профессионального образования
Всероссийский Заочный Финансово-Экономический институт
Филиал г. Тула
Контрольная работа
по дисциплине "Эконометрика"
Вариант 8
Выполнила:
Проверил:
Тула
2008
Задача 1
По предприятиям легкой промышленности региона получена информация, характеризующая зависимость объема выпуска продукции (![]() , млн. руб.) от объема капиталовложений (
, млн. руб.) от объема капиталовложений (![]() , млн. руб.).
, млн. руб.).
Требуется:
1. Найти параметры уравнения линейной регрессии, дать экономическую интерпретацию коэффициента регрессии.
2. Вычислить остатки; найти остаточную сумму квадратов; оценить дисперсию остатков ![]() ; построить график остатков.
; построить график остатков.
3. Проверить выполнение предпосылок МНК.
4. Осуществить проверку значимости параметров уравнения регрессии с помощью t-критерия Стьюдента ![]()
5. Вычислить коэффициент детерминации, проверить значимость уравнения регрессии с помощью ![]() -критерия Фишера
-критерия Фишера ![]() , найти среднюю относительную ошибку аппроксимации. Сделать вывод о качестве модели.
, найти среднюю относительную ошибку аппроксимации. Сделать вывод о качестве модели.
6. Осуществить прогнозирование среднего значения показателя ![]() при уровне значимости
при уровне значимости ![]() , если прогнозное значения фактора Х составит 80% от его максимального значения.
, если прогнозное значения фактора Х составит 80% от его максимального значения.
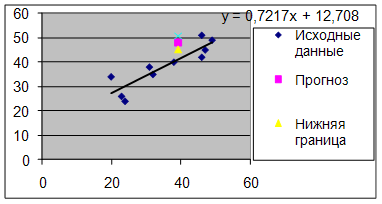
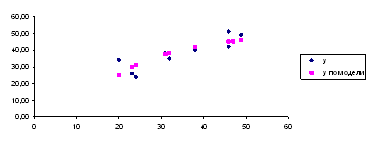
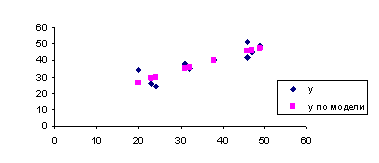
7. Представить графически: фактические и модельные значения ![]() точки прогноза.
точки прогноза.
8. Составить уравнения нелинейной регрессии:
· гиперболической;
· степенной;
· показательной.
Привести графики построенных уравнений регрессии.
9. Для указанных моделей найти коэффициенты детерминации и средние относительные ошибки аппроксимации. Сравнить модели по этим характеристикам и сделать вывод.
Вариант 8
|
| 17 | 22 | 10 | 7 | 12 | 21 | 14 | 7 | 20 | 3 |
|
| 26 | 27 | 22 | 19 | 21 | 26 | 20 | 15 | 30 | 13 |
Решение:
1. Уравнение линейной регрессии имеет следующий вид:
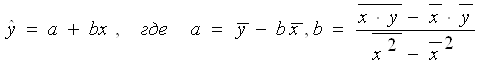
Таблица 1
| №наблюдения | X | Y | X2 | X·Y |
| 1 | 17 | 26 | 289 | 442 |
| 2 | 22 | 27 | 484 | 594 |
| 3 | 10 | 22 | 100 | 220 |
| 4 | 7 | 19 | 49 | 133 |
| 5 | 12 | 21 | 144 | 252 |
| 6 | 21 | 26 | 441 | 546 |
| 7 | 14 | 20 | 196 | 280 |
| 8 | 7 | 15 | 49 | 105 |
| 9 | 20 | 30 | 400 | 600 |
| 10 | 3 | 13 | 9 | 39 |
| Сумма | 133 | 219 | 2161 | 3211 |
| Ср. значение | 13,3 | 21,9 | 216,1 | 321,1 |
Найдем b:
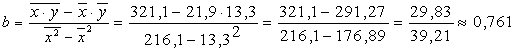
Тогда ![]()
Уравнение линейной регрессии имеет вид: ŷx=11,779+0,761x.
Коэффициент регрессии показывает среднее изменение результата с изменением фактора на одну единицу.
С увеличением объема капиталовложений на 1 млн. рублей объем выпускаемой продукции увеличится в среднем на 761 тыс. рублей.
2. Вычислим остатки при помощи. Получим:
Таблица 2
| ВЫВОД ОСТАТКА | |||
| Наблюдение |
| Остатки |
|
| 1 | 24,72 | 1,284 | 1,649 |
| 2 | 28,52 | -1,521 | 2,313 |
| 3 | 19,39 | 2,611 | 6,817 |
| 4 | 17,11 | 1,894 | 3,587 |
| 5 | 20,91 | 0,089 | 0,008 |
| 6 | 27,76 | -1,76 | 3,098 |
| 7 | 22,43 | -2,433 | 5,919 |
| 8 | 17,11 | -2,106 | 4,435 |
| 9 | 27 | 3,001 | 9,006 |
| 10 | 14,06 | -1,062 | 1,128 |
| Сумма | 219 | -0,003 | 37,961 |
Найдем остаточную сумму квадратов:
![]()
Дисперсия остатков равна:
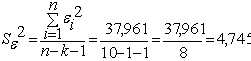 .
.
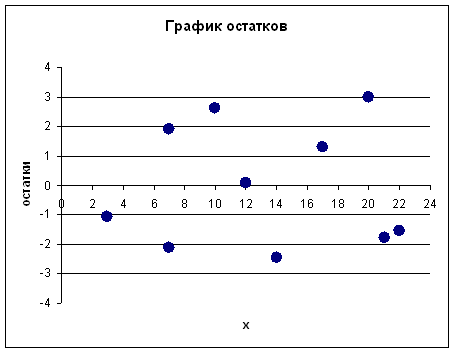
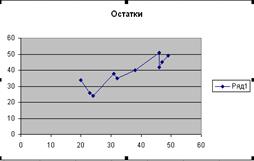
График остатков имеет следующий вид:
График 1
Похожие работы
объема экспериментальных исследований. Применение современной вычислительной техники позволяет в ряде случаев упростить процедуру определения релаксационных констант. Особенно этот метод эффективен, с нашей точки зрения, при изучении релаксационных процессов в модифицированных полимерных материалах, когда известны релаксационные константы полимера-связующего. Суть подхода в определении U, Tm и B ...
... регрессией SSR = ∑(ỹ-y)2 = 3990,5; Остатки, необъясненный разброс SSЕ = ∑(ỹ-yi)2 = 1407,25; Общий разброс данных SSY = ∑(yi-y)2 = 5397,85; Для анализа общего качества оценной линейной регрессии найдем коэффициент детерминации: R2 = SSR/SSY = 0.7192; Разброс данных объясняется линейной моделью на 72% и на 28% – случайными ошибками. Вывод: Качество модели хорошее ...
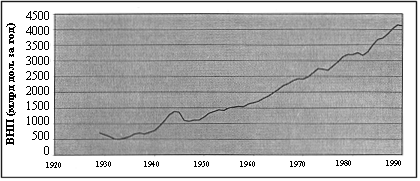
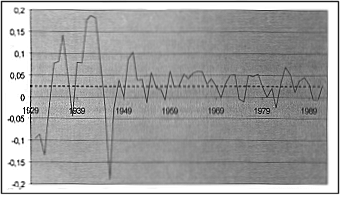
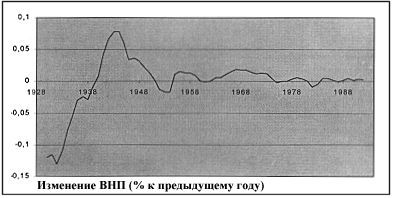
... темпа роста ВНП за рассматриваемый период и, наконец, расчет оптимальной (с наибольшей корреляцией) линии тенденции внутри рассматриваемого периода. Особенности прогноза динамики ВНП методом линейной регрессии Приведенный выше анализ позволяет также высказать ряд соображений, касающихся прогноза динамики ВНП. Имеется в виду использование полученных количественных моделей для определения величины ...
нты детерминации, коэффициенты эластичности и средние относительные ошибки аппроксимации. Сравнить модели по этим характеристикам и сделать вывод. Решение 1. Уравнение линейной регрессии имеет вид: = а0 + а1x. Построим линейную модель. Для удобства выполнения расчетов предварительно упорядочим всю таблицу исходных данных по возрастанию факторной переменной Х (Данные => Сортировка). ( ...


0 комментариев