Навигация
Проверим выполнение предпосылок МНК
3. Проверим выполнение предпосылок МНК.
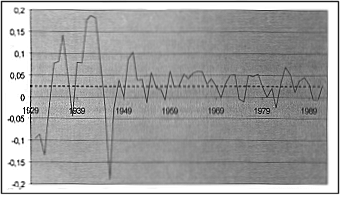
· Случайный характер остатков.
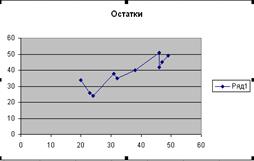
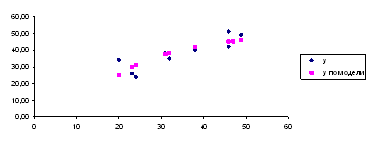
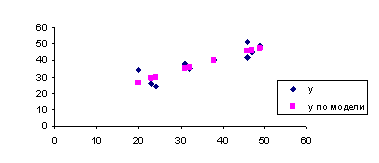
Случайный характер остатков εi проверяется по графику. Как видно из графика 1 в расположении точек εiнетнаправленности (на графике получена горизонтальная полоса). Следовательно,εi– случайные величины и применение МНК оправдано.
· Средняя величина остатков или математическое ожидание равно нулю.
Так как расположение остатков на графике не имеет направленности (расположены на графике в виде горизонтальной полосы), то они независимы от значений фактора xi. Следовательно, модель адекватна.
· Проверка гомоскедастичности остатков.
Выборка у нас малого объема, поэтому для оценки гомоскедастичность остатков используем метод Голдфельда - Квандта.
1) Упорядочим n = 10 наблюдений в порядке возрастания х.
2) Разделим на две группы - с большим и меньшим x, и для каждой группы определим уравнения регрессии.
Таблица 3
|
| х | y | x·y | x2 | ŷ | εi=yi-ŷi | ε2 |
| 1 | 3 | 13 | 39 | 9 | 13,181 | -0,181 | 0,033 |
| 2 | 7 | 19 | 133 | 49 | 17,197 | 1,803 | 3,251 |
| 3 | 7 | 15 | 105 | 49 | 17,197 | -2,197 | 4,827 |
| 4 | 10 | 22 | 220 | 100 | 20,209 | 1,791 | 3,208 |
| 5 | 12 | 21 | 252 | 144 | 22,217 | -1,217 | 1,481 |
| Сумма | 39 | 90 | 749 | 351 | 12,799 | ||
| Ср.знач | 7,8 | 18 | 149,8 | 70,2 | |||
|
| х | y | x·y | x2 | ŷ | εi=yi-ŷi | ε2 |
| 1 | 14 | 20 | 280 | 196 | 21,672 | -1,672 | 2,796 |
| 2 | 17 | 26 | 442 | 289 | 24,252 | 1,748 | 3,056 |
| 3 | 20 | 30 | 600 | 400 | 26,832 | 3,168 | 10,036 |
| 4 | 21 | 26 | 546 | 441 | 27,692 | -1,692 | 2,863 |
| 5 | 22 | 27 | 594 | 484 | 28,552 | -1,552 | 2,409 |
| Сумма | 94 | 129 | 2462 | 1810 | 21,159 | ||
| Ср.знач | 18,8 | 25,8 | 492,4 | 362 |
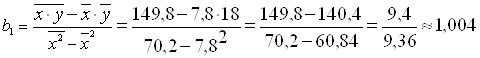
![]()
![]()
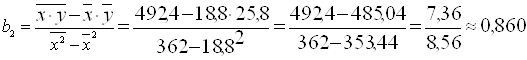
![]()
![]()
3) Рассчитаем остаточные суммы квадратов для каждой регрессии.
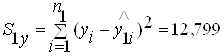 ,
,
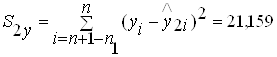 .
.
4) Вычислим F- распределения.
Fнабл=S2ŷ/S1ŷ =1,653.
5) Произведем сравнение Fнабл и Fтабл.
1,653<5,32 (при k1=1 и k2=n–2=10–2=8), следовательно, гетероскедастичность места не имеет, т.е. дисперсия остатков гомоскедастична.
· Отсутствие автокорреляции.
Отсутствие автокорреляции проверяется по d-критерию Дарбина - Уотсона:
Таблица 4
|
| εi | εi-1 | εi- εi-1 | (εi- εi-1)2 |
| 1 | 1,284 | |||
| 2 | -1,521 | 1,284 | -2,805 | 7,868 |
| 3 | 2,611 | -1,521 | 4,132 | 17,073 |
| 4 | 1,894 | 2,611 | -0,717 | 0,5141 |
| 5 | 0,089 | 1,894 | -1,805 | 3,258 |
| 6 | -1,760 | 0,089 | -1,849 | 3,4188 |
| 7 | -2,433 | -1,760 | -0,673 | 0,4529 |
| 8 | -2,106 | -2,433 | 0,327 | 0,1069 |
| 9 | 3,001 | -2,106 | 5,107 | 26,081 |
| 10 | -1,062 | 3,001 | -4,063 | 16,508 |
| Сумма | 75,282 |
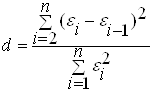 ; d=75,282/37,961=1,983.
; d=75,282/37,961=1,983.
Так как d-критерий меньше двух, то мы наблюдаем присутствие положительной автокорреляции.
· Остатки подчиняются нормальному закону распределения.
4. Осуществить проверку значимости параметров уравнения регрессии с помощью t-критерия Стьюдента ![]()
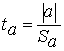 ;
; 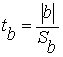 ,
,
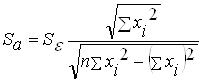 ;
; 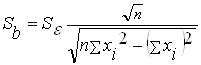 ,
,
где 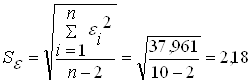
Тогда 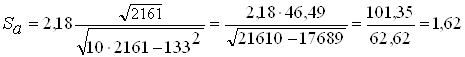 ,
, 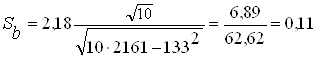 ;
; ![]() и
и ![]()
tтабл=2,3060 (при 10-2=8 степенях свободы); tа и tb> tтабл, что говорит о значимости параметров модели.
5. Коэффициент детерминации находится по формуле:
 .
.
Данные возьмем из таблицы 5:
Таблица 5
| № | x | y |
|
|
|
|
|
|
| 1 | 17 | 26 | 3,7 | 4,1 | 13,69 | 16,81 | 1,284 | 4,938 |
| 2 | 22 | 27 | 8,7 | 5,1 | 75,69 | 26,01 | -1,521 | 5,633 |
| 3 | 10 | 22 | -3,3 | 0,1 | 10,89 | 0,01 | 2,611 | 11,868 |
| 4 | 7 | 19 | -6,3 | -2,9 | 39,69 | 8,41 | 1,894 | 9,968 |
| 5 | 12 | 21 | -1,3 | -0,9 | 1,69 | 0,81 | 0,089 | 0,424 |
| 6 | 21 | 26 | 7,7 | 4,1 | 59,29 | 16,81 | -1,760 | 6,769 |
| 7 | 14 | 20 | 0,7 | -1,9 | 0,49 | 3,61 | -2,433 | 12,165 |
| 8 | 7 | 15 | -6,3 | -6,9 | 39,69 | 47,61 | -2,106 | 14,040 |
| 9 | 20 | 30 | 6,7 | 8,1 | 44,89 | 65,61 | 3,001 | 10,003 |
| 10 | 3 | 13 | -10,3 | -8,9 | 106,09 | 79,21 | -1,062 | 8,169 |
| Сумма | 133 | 219 | 392,1 | 264,9 |
| 83,979 | ||
| Ср. знач. | 13,3 | 21,9 |
|
|
|
|
|
|
Для проверки значимости модели используем F-критерий Фишера:
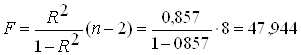 .
.
Fтабл=5,32 (k1=1, k2=8 степенями свободы);
F>Fтабл, что говорит о значимости уравнения регрессии.
Среднюю относительную ошибку аппроксимации находим по формуле:
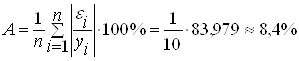 ;
;
В среднем расчетные значения отклоняются от фактических на 8,4%.
Поскольку найденная средняя относительная ошибка аппроксимации находится в интервале от 5 до 10, то можно утверждать, что модель имеет хорошее качество.
6. Ширина доверительного интервала находится по формулам:
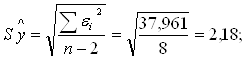
![]()
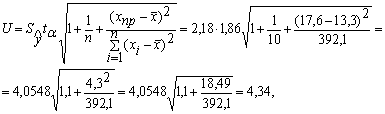
где tα=1,86 приm=n-2=8 и α=0,1
Т.о.
![]()
Верхн. граница: 25,173+4,34=29,513
Нижн. граница: 25,173-4,34=20,833
Таблица 6
| Нижняя граница | Прогноз | Верхняя граница |
| 20,83 | 25,17 | 29,51 |
Похожие работы
объема экспериментальных исследований. Применение современной вычислительной техники позволяет в ряде случаев упростить процедуру определения релаксационных констант. Особенно этот метод эффективен, с нашей точки зрения, при изучении релаксационных процессов в модифицированных полимерных материалах, когда известны релаксационные константы полимера-связующего. Суть подхода в определении U, Tm и B ...
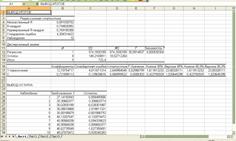
... регрессией SSR = ∑(ỹ-y)2 = 3990,5; Остатки, необъясненный разброс SSЕ = ∑(ỹ-yi)2 = 1407,25; Общий разброс данных SSY = ∑(yi-y)2 = 5397,85; Для анализа общего качества оценной линейной регрессии найдем коэффициент детерминации: R2 = SSR/SSY = 0.7192; Разброс данных объясняется линейной моделью на 72% и на 28% – случайными ошибками. Вывод: Качество модели хорошее ...
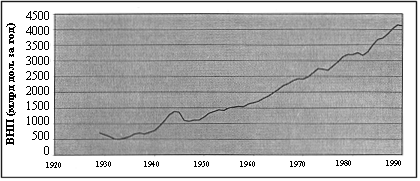
... темпа роста ВНП за рассматриваемый период и, наконец, расчет оптимальной (с наибольшей корреляцией) линии тенденции внутри рассматриваемого периода. Особенности прогноза динамики ВНП методом линейной регрессии Приведенный выше анализ позволяет также высказать ряд соображений, касающихся прогноза динамики ВНП. Имеется в виду использование полученных количественных моделей для определения величины ...
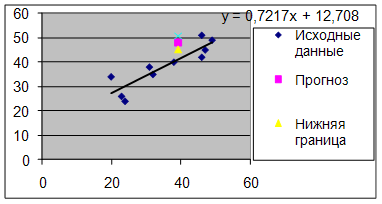
нты детерминации, коэффициенты эластичности и средние относительные ошибки аппроксимации. Сравнить модели по этим характеристикам и сделать вывод. Решение 1. Уравнение линейной регрессии имеет вид: = а0 + а1x. Построим линейную модель. Для удобства выполнения расчетов предварительно упорядочим всю таблицу исходных данных по возрастанию факторной переменной Х (Данные => Сортировка). ( ...
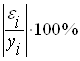


0 комментариев