Навигация
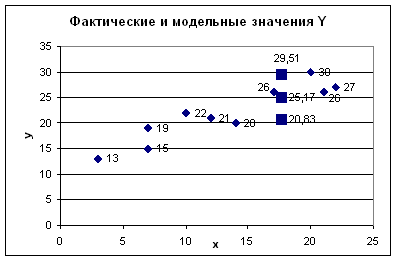
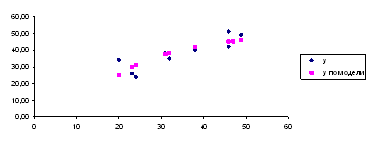
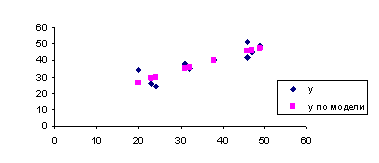
Фактические и модельные значения Y, точки прогноза представлены на графике 2
7. Фактические и модельные значения Y, точки прогноза представлены на графике 2.
График 2
8. Составить уравнения нелинейной регрессии:
· Гиперболической
Уравнение показательной кривой имеет вид: ŷ = a + b/x.
Произведем линеаризацию модели путем замены Х = 1/х.
Тогда уравнение примет вид: ŷ = a + bХ- линейное уравнение регрессии.
Данные, необходимые для нахождения параметров приведены в таблице 6
Таблица 7
| № | y | x | X | X2 | Xy | ŷ | εi | εi2 |
|
| 1 | 26 | 17 | 0,0588 | 0,0035 | 1,5294 | 24,41 | 1,59 | 2,52 | 6,11 |
| 2 | 27 | 22 | 0,0455 | 0,0021 | 1,2273 | 25,10 | 1,90 | 3,61 | 7,04 |
| 3 | 22 | 10 | 0,1000 | 0,0100 | 2,2000 | 22,29 | -0,29 | 0,09 | 1,33 |
| 4 | 19 | 7 | 0,1429 | 0,0204 | 2,7143 | 20,09 | -1,09 | 1,18 | 5,72 |
| 5 | 21 | 12 | 0,0833 | 0,0069 | 1,7500 | 23,15 | -2,15 | 4,63 | 10,24 |
| 6 | 26 | 21 | 0,0476 | 0,0023 | 1,2381 | 24,99 | 1,01 | 1,02 | 3,89 |
| 7 | 20 | 14 | 0,0714 | 0,0051 | 1,4286 | 23,76 | -3,76 | 14,16 | 18,82 |
| 8 | 15 | 7 | 0,1429 | 0,0204 | 2,1429 | 20,09 | -5,09 | 25,88 | 33,91 |
| 9 | 30 | 20 | 0,0500 | 0,0025 | 1,5000 | 24,87 | 5,13 | 26,35 | 17,11 |
| 10 | 13 | 3 | 0,3333 | 0,1111 | 4,3333 | 10,28 | 2,72 | 7,38 | 20,90 |
| Сумма | 219 | 133 | 1,0757 | 0,1843 | 20,0638 |
|
| 86,82 | 125,07 |
| Ср.знач. | 21,9 | 13,3 | 0,1076 | 0,0184 | 2,0064 |
|
|
|
|
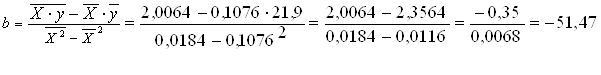
Значение параметров а и b линейной модели определим по формулам:
![]()
Уравнение регрессии будет иметь вид ŷ = 27,44 – 51,47 X.
Перейдем к исходным переменным, получим уравнение гиперболической модели:
![]() .
.
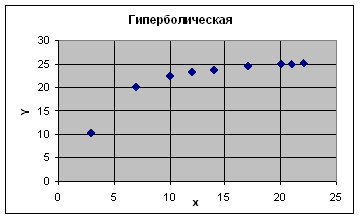 График 3
График 3
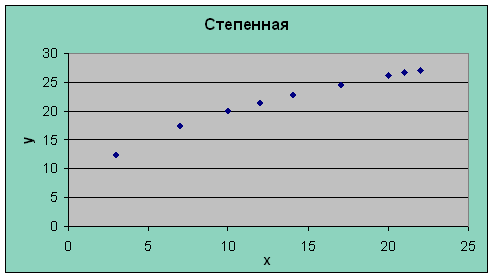
Степенная
Уравнение степенной модели имеет вид: ŷ = a · xb
Для построения этой модели необходимо произвести линеаризацию переменных. Для этого произведем логарифмирование обеих частей уравнения:
lg ŷ = lg a + b lg x
Обозначим Y = lg ŷ; A = lg a; X = lg x
Тогда уравнение примет вид: Y = A + bX - линейное уравнение регрессии.
Рассчитаем его параметры, используя данные таблицы 8:
Таблица 8
| № | y | x | Y | X | YX | X2 | ŷ | εi | εi2 |
|
| 26 | 17 | 1,4150 | 1,2304 | 1,7411 | 1,5140 | 24,545 | 1,45 | 2,12 | 5,60 | |
| 27 | 22 | 1,4314 | 1,3424 | 1,9215 | 1,8021 | 27,142 | -0,14 | 0,02 | 0,52 | |
| 22 | 10 | 1,3424 | 1,0000 | 1,3424 | 1,0000 | 19,957 | 2,04 | 4,17 | 9,29 | |
| 19 | 7 | 1,2788 | 0,8451 | 1,0807 | 0,7142 | 17,365 | 1,63 | 2,67 | 8,60 | |
| 21 | 12 | 1,3222 | 1,0792 | 1,4269 | 1,1646 | 21,427 | -0,43 | 0,18 | 2,04 | |
| 26 | 21 | 1,4150 | 1,3222 | 1,8709 | 1,7483 | 26,654 | -0,65 | 0,43 | 2,51 | |
| 20 | 14 | 1,3010 | 1,1461 | 1,4911 | 1,3136 | 22,755 | -2,76 | 7,59 | 13,78 | |
| 15 | 7 | 1,1761 | 0,8451 | 0,9939 | 0,7142 | 17,365 | -2,37 | 5,59 | 15,77 | |
| 30 | 20 | 1,4771 | 1,3010 | 1,9218 | 1,6927 | 26,151 | 3,85 | 14,81 | 12,83 | |
| 13 | 3 | 1,1139 | 0,4771 | 0,5315 | 0,2276 | 12,479 | 0,52 | 0,27 | 4,01 | |
| Сумма | 219 | 133 | 13,2729 | 10,5887 | 14,3218 | 11,8913 |
|
| 37,86 | 74,94 |
| Ср.знач. | 21,9 | 13,3 | 1,3273 | 1,0589 | 1,4322 | 1,1891 |
|
|
|
|
Значение параметров А и b линейной модели определим по формулам:
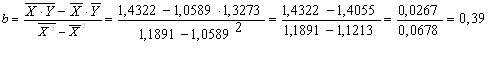
Значение параметров А и b линейной модели определим по формулам:
![]()
Уравнение регрессии имеет вид: Y=0,91 + 0,39X
Перейдем к исходным переменным x и y, выполнив потенцирование данного уравнения:
ŷ=100,91 · x0,39
ŷ =8,13 · x0,39.
График 4
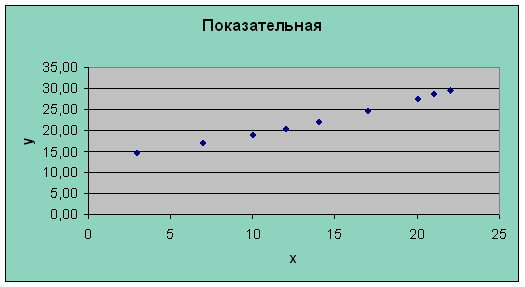
· Показательная
Уравнение показательной кривой имеет вид: ŷ = a · bx
Для построения этой модели необходимо произвести линеаризацию переменных. Для этого произведем логарифмирование обеих частей уравнения:
lg ŷ = lg a + x lg b
Обозначим Y = lg ŷ; A = lg a; B = lg b
Тогда уравнение примет вид: Y = A + Bx - линейное уравнение регрессии.
Данные, необходимы для нахождения параметров, приведены в таблице 9.
Таблица 9
| №наблюдения | y | x | Y | Yx | x2 | ŷ | εi | εi2 |
|
| 1 | 26 | 17 | 1,4150 | 24,0545 | 289 | 24,564 | 1,436 | 2,06 | 5,52 |
| 2 | 27 | 22 | 1,4314 | 31,4900 | 484 | 29,600 | -2,600 | 6,76 | 9,63 |
| 3 | 22 | 10 | 1,3424 | 13,4242 | 100 | 18,920 | 3,080 | 9,49 | 14,00 |
| 4 | 19 | 7 | 1,2788 | 8,9513 | 49 | 16,917 | 2,083 | 4,34 | 10,96 |
| 5 | 21 | 12 | 1,3222 | 15,8666 | 144 | 20,385 | 0,615 | 0,38 | 2,93 |
| 6 | 26 | 21 | 1,4150 | 29,7144 | 441 | 28,516 | -2,516 | 6,33 | 9,68 |
| 7 | 20 | 14 | 1,3010 | 18,2144 | 196 | 21,964 | -1,964 | 3,86 | 9,82 |
| 8 | 15 | 7 | 1,1761 | 8,2326 | 49 | 16,917 | -1,917 | 3,68 | 12,78 |
| 9 | 30 | 20 | 1,4771 | 29,5424 | 400 | 27,472 | 2,528 | 6,39 | 8,43 |
| 10 | 13 | 3 | 1,1139 | 3,3418 | 9 | 14,573 | -1,573 | 2,47 | 12,10 |
| Сумма | 219 | 133 | 13,2729 | 182,8324 | 2161 |
|
| 45,75 | 95,84 |
| Ср.знач. | 21,9 | 13,3 | 1,3273 | 18,2832 | 216,1 |
|
|
|
|
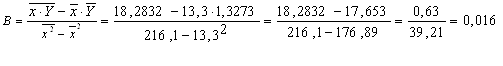
Значение параметров А и B линейной модели определим по формулам:
![]()
Уравнение регрессии будет иметь вид: Y = 1,115 + 0,016x.
Перейдем к исходным переменным x и y, выполнив потенцирование данного уравнения:
ŷ =101,115·(100,016)x;
ŷ =13,03·1,038x.
График 5
9. Для указанных моделей найти: R2 – коэффициент детерминации и средние относительные ошибки аппроксимации А.
![]() для всех моделей = 264,9 (см. таблицу 5).
для всех моделей = 264,9 (см. таблицу 5).
· Степенная модель (см. таблицу 8):
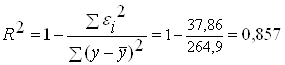 ;
;
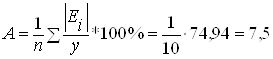 ;
;
· Показательная модель (см.таблицу 9):
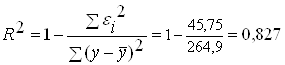 ;
;
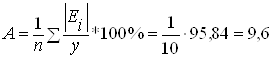 ;
;
· Гиперболическая модель (см. таблицу 7):
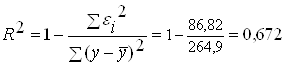
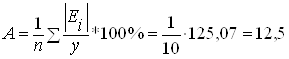 .
.
Таблица 10
| Параметры Модели | Коэффициент детерминации R2 | Средняя относительная ошибка аппроксимации А |
| 1. Степенная | 0,857 | 7,5 |
| 2. Показательная | 0,827 | 9,6 |
| 3. Гиперболическая | 0,672 | 12,5 |
Коэффициент детерминации показывает долю вариации результативного признака, находящегося под воздействием изучаемых факторов. Чем ближе R2 к 1, тем выше качество модели.
Чем выше рассеяние эмпирических точек вокруг теоретической линии регрессии, тем меньше средняя ошибка аппроксимации. Ошибка аппроксимации меньше 7% свидетельствует о хорошем качестве модели.
При сравнении гиперболической, степенной и показательной моделей по данным характеристикам мы видим, что наибольшее значение коэффициента детерминации R2 и наименьшую ошибку аппроксимации имеет степенная модель, следовательно, ее можно считать лучшей.
Задача 2
Даны две СФМ, которые заданы в виде матриц коэффициентов модели. Необходимо записать системы одновременных уравнений и проверить обе системы на идентифицируемость.
Таблица 1
| № варианта | № уравнения | Задача 2а | Задача 2б | ||||||||||||
| переменные | переменные | ||||||||||||||
| y1 | y2 | y3 | x1 | x2 | x3 | x4 | y1 | y2 | y3 | x1 | x2 | x3 | x4 | ||
| 8 | 1 | -1 | b12 | b13 | 0 | a12 | a13 | 0 | -1 | 0 | b13 | a11 | 0 | a13 | a14 |
| 2 | 0 | -1 | b23 | a21 | a22 | 0 | a24 | b21 | -1 | b23 | 0 | a22 | 0 | a24 | |
| 3 | 0 | b32 | -1 | a31 | a32 | a33 | 0 | b31 | 0 | -1 | a31 | 0 | a33 | a34 | |
Решение
2а)  , тогда система уравнений будет иметь вид:
, тогда система уравнений будет иметь вид:
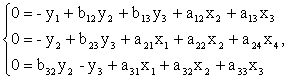
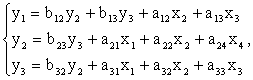
Модель имеет 3 эндогенные (y1, y2, y3) и 4 экзогенные (x1, x2, x3, x4) переменные. Проверим каждое уравнение на необходимое и достаточное условие идентификации.
1 уравнение: y1= b12y2+b13y3+a12x2+a13x3;
Необходимое условие: D + 1 = H
Эндогенные переменные: y1, y2, y3; H=3
Отсутствующие экзогенные переменные: х1, х4; D=2
2+1=3 - условие необходимости выполнено.
Достаточное условие: В уравнении отсутствуют х1, х4. Построим матрицу из коэффициентов для второго и третьего уравнения:
Таблица 2
| Уравнение | переменные | |
| х1 | х4 | |
| 2 | a21 | a24 |
| 3 | a31 | 0 |
Найдем определитель: ![]() , ранг =2, следовательно, условие достаточности выполнено.
, ранг =2, следовательно, условие достаточности выполнено.
1-ое уравнение идентифицируемо.
2 уравнение: y2= b23 y3+a21x1+a22x2+a24x4 ;
Необходимое условие: D + 1 = H
Эндогенные переменные: y2, y3; H=2
Отсутствующие экзогенные переменные: х3; D=1
1+1=2 - условие необходимости выполнено.
Достаточное условие: В уравнении отсутствуют y1, х3. Построим матрицу из коэффициентов для первого и третьего уравнения:
Таблица 3
| Уравнение | переменные | |
| y1 | х3 | |
| 1 | -1 | a13 |
| 3 | 0 | a33 |
Найдем определитель: ![]() , ранг =2, следовательно, условие достаточности выполнено.
, ранг =2, следовательно, условие достаточности выполнено.
2-ое уравнение идентифицируемо.
3 уравнение: y3= b32y2+a31x1+a32x2+a33x3;
Необходимое условие: D + 1 = H
Эндогенные переменные: y2, y3; H=2
Отсутствующие экзогенные переменные: х4; D=1
1+1=2 - условие необходимости выполнено.
Достаточное условие: В уравнении отсутствуют y1, х4. Построим матрицу из коэффициентов для первого и второго уравнения:
Таблица 4
| Уравнение | переменные | |
| х1 | х4 | |
| 1 | -1 | 0 |
| 2 | 0 | a24 |
Найдем определитель: ![]() , ранг =2, следовательно, условие достаточности выполнено.
, ранг =2, следовательно, условие достаточности выполнено.
3-е уравнение идентифицируемо.
В целом вся система уравнений является идентифицируемой.
Решение
2б)  ,
,
Тогда система уравнений будет иметь вид:
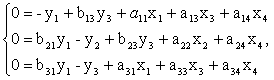
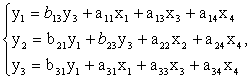
Модель имеет 3 эндогенные (y1, y2, y3) и 4 экзогенные (x1, x2, x3, x4) переменные. Проверим каждое уравнение на необходимое и достаточное условие идентификации.
1 уравнение: y1= b13y3+a11x1+a13x3+a14x4;
Необходимое условие: D + 1 = H
Эндогенные переменные: y1, y3; H=2
Отсутствующие экзогенные переменные: х2; D=1
1+1=2 - условие необходимости выполнено.
Достаточное условие: В уравнении отсутствуют y2, х2. Построим матрицу из коэффициентов для второго и третьего уравнения:
Таблица 5
| Уравнение | переменные | |
| y2 | х2 | |
| 2 | -1 | a22 |
| 3 | 0 | 0 |
Найдем определитель: ![]() , следовательно, условие достаточности НЕ выполнено.
, следовательно, условие достаточности НЕ выполнено.
1-ое уравнение НЕидентифицируемо.
2 уравнение: y2= b11 y1+b23y3+a22x2+a24x4 ;
Необходимое условие: D + 1 = H
Эндогенные переменные: y1, y2, y3; H=3
Отсутствующие экзогенные переменные: x1, х3; D=2
2+1=3 - условие необходимости выполнено.
Достаточное условие: В уравнении отсутствуют x1, х3. Построим матрицу из коэффициентов для первого и третьего уравнения:
Таблица 6
| Уравнение | переменные | |
| x1 | х3 | |
| 1 | a11 | a13 |
| 3 | a31 | a33 |
Найдем определитель: ![]() , ранг =2, следовательно, условие достаточности выполнено.
, ранг =2, следовательно, условие достаточности выполнено.
2-ое уравнение идентифицируемо.
3 уравнение: y3= b31y2+a31x1+a33x3+a34x4;
Необходимое условие: D + 1 = H
Эндогенные переменные: y1, y3; H=2
Отсутствующие экзогенные переменные: х2; D=1
1+1=2 - условие необходимости выполнено.
Достаточное условие: В уравнении отсутствуют y1, х4. Построим матрицу из коэффициентов для первого и второго уравнения:
Таблица 7
| Уравнение | переменные | |
| y2 | х2 | |
| 1 | 0 | 0 |
| 2 | -1 | a22 |
Найдем определитель: ![]() , следовательно, условие достаточности НЕ выполнено
, следовательно, условие достаточности НЕ выполнено
3-е уравнение НЕидентифицируемо.
В целом вся система уравнений является НЕидентифицируемой, так как первое и третье уравнение – НЕидентифицируемы.
2в) По данным, используя косвенный метод наименьших квадратов, построить структурную форму модели вида: y1=a01+b12y2+a11x1+ε1;
y2=a02+b21y1+a22x2+ε2
Таблица 8
| Вариант | n | y1 | y2 | x1 | x2 |
| 8 | 1 | 51.3 | 39.4 | 3 | 10 |
| 2 | 112.4 | 77.9 | 10 | 13 | |
| 3 | 67.5 | 45.2 | 5 | 3 | |
| 4 | 51.4 | 37.7 | 3 | 7 | |
| 5 | 99.3 | 66.1 | 9 | 6 | |
| 6 | 57.1 | 39.6 | 4 | 1 |
Решение
1) Структурную форму модели (СФМ) преобразуем в приведенную форму модели (ПФМ):
Для этого из второго уравнения выражаем y2 и подставляем его в первое, а из первого выражаем y1 и подставляем его во второе уравнение. Получим:
y1=δ11x1+ δ12x2+u1;
y2=δ21x1+ δ22x2+u2,
где u1 и u1 –случайные ошибки ПФМ.
Здесь


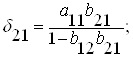
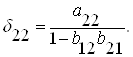
2) В каждом уравнение ПФМ с помощью МНК определим δ – коэффициент.
Для первого уравнения:
![]()
![]()
![]() .
.
Для решения системы уравнений требуются вспомогательные расчеты, которые представлены в таблице 9, 10.
Таблица 9
| n | y1 | y2 | x1 | x2 |
| 1 | 51,3 | 39,4 | 3 | 10 |
| 2 | 112,4 | 77,9 | 10 | 13 |
| 3 | 67,5 | 45,2 | 5 | 3 |
| 4 | 51,4 | 37,7 | 3 | 7 |
| 5 | 99,3 | 66,1 | 9 | 6 |
| 6 | 57,1 | 39,6 | 4 | 1 |
| Сумма | 439 | 305,9 | 34 | 40 |
| Сред. знач. | 73,17 | 50,98 | 5,67 | 6,67 |
Для упрощения расчетов удобнее работать с отклонениями от средних уровней:
∆у = у - уср; ∆х = х - хср
Таблица 10
| n | ∆y1 | ∆y2 | ∆x1 | ∆x2 | ∆y1∆x1 | ∆x12 | ∆x1∆x2 | ∆y1∆x2 | ∆y2∆x1 | ∆y2∆x2 | ∆x22 |
| 1 | -21,9 | -11,6 | -2,7 | 3,3 | 58,31 | 7,11 | -8,89 | -72,89 | 30,89 | -38,61 | 11,11 |
| 2 | 39,2 | 26,9 | 4,3 | 6,3 | 170,0 | 18,78 | 27,44 | 248,48 | 116,64 | 170,47 | 40,11 |
| 3 | -5,7 | -5,8 | -0,7 | -3,7 | 3,78 | 0,44 | 2,44 | 20,78 | 3,86 | 21,21 | 13,44 |
| 4 | -21,8 | -13,3 | -2,7 | 0,3 | 58,04 | 7,11 | -0,89 | -7,26 | 35,42 | -4,43 | 0,11 |
| 5 | 26,1 | 15,1 | 3,3 | -0,7 | 87,11 | 11,11 | -2,22 | -17,42 | 50,39 | -10,08 | 0,44 |
| 6 | -16,1 | -11,4 | -1,7 | -5,7 | 26,78 | 2,78 | 9,44 | 91,04 | 18,97 | 64,51 | 32,11 |
| ∑ | -0,2 | -0,1 | -0,2 | -0,2 | 404,03 | 47,33 | 27,33 | 262,73 | 256,17 | 203,07 | 97,33 |
С учетом приведенных данных получим:
404,03 = 47,33δ11 + 27,33δ12
262,73 = 27,33δ11 + 97,33δ12
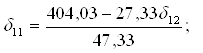
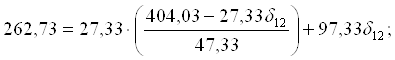
δ12 = 0,36;
![]()
С учетом этого первое уравнение ПФМ примет вид:
y1 = 8,33х1 + 0,36х2 + u1
Для второго уравнения определим δ – коэффициент с помощью МНК:
![]()
![]()
![]()
Для дальнейших расчетов данные берем из таблицы 9, 10. Получим:
256,17=47,33δ21+27,33δ22
203,07=27,33δ21+97,33δ22
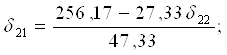
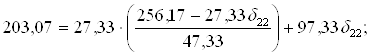
δ22 = 0,68;
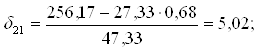
Второе уравнение ПФМ примет вид:
у2 = 5,02х1 + 0,68х2 + u2
3) Выполним переход от ПФМ к СПФМ. Для этого из последнего уравнения найдем х2:
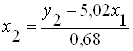
Найденное х2 подставим в первое уравнение.
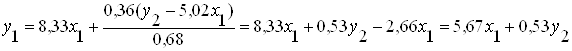 ,
,
тогда b12=0,53; a11=5,67
Из первого уравнения ПФМ найдем х1
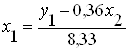
Подставим во второе уравнение ПФМ
 ,
,
тогда b21=0,6; a22=0,46
4) Свободные члены СФМ найдем из уравнения:
а01 = у1ср - b12у2ср - а11х1ср = 73,17 – 0,53 50,98 - 5,67 5,67 = 14,00;
а02 = у2ср - b21у1ср - а22х2ср = 50,98 - 0,6 73,17 - 0,46 6,67 = 4,00.
5) Записываем СФМ в окончательном виде:
y1=a01 + b12y2 + a11x1 + ε1;
y2=a02 + b21y1 + a22x2 + ε2.
y1 =14+ 0,53y2 + 5,67x1 + ε1;
y2 = 4+ 0,6y1 + 0,46x2 + ε2.
Похожие работы
объема экспериментальных исследований. Применение современной вычислительной техники позволяет в ряде случаев упростить процедуру определения релаксационных констант. Особенно этот метод эффективен, с нашей точки зрения, при изучении релаксационных процессов в модифицированных полимерных материалах, когда известны релаксационные константы полимера-связующего. Суть подхода в определении U, Tm и B ...
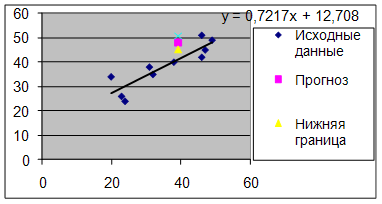
... регрессией SSR = ∑(ỹ-y)2 = 3990,5; Остатки, необъясненный разброс SSЕ = ∑(ỹ-yi)2 = 1407,25; Общий разброс данных SSY = ∑(yi-y)2 = 5397,85; Для анализа общего качества оценной линейной регрессии найдем коэффициент детерминации: R2 = SSR/SSY = 0.7192; Разброс данных объясняется линейной моделью на 72% и на 28% – случайными ошибками. Вывод: Качество модели хорошее ...
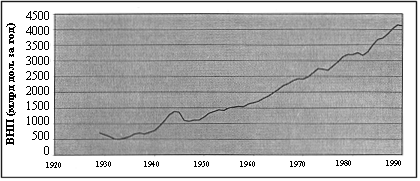
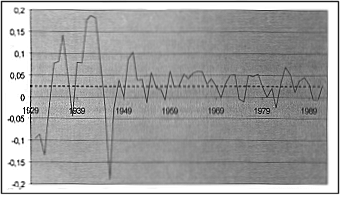
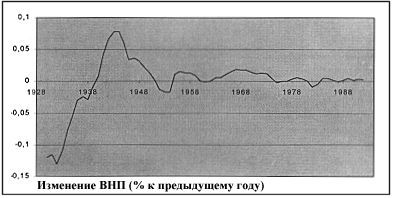
... темпа роста ВНП за рассматриваемый период и, наконец, расчет оптимальной (с наибольшей корреляцией) линии тенденции внутри рассматриваемого периода. Особенности прогноза динамики ВНП методом линейной регрессии Приведенный выше анализ позволяет также высказать ряд соображений, касающихся прогноза динамики ВНП. Имеется в виду использование полученных количественных моделей для определения величины ...
нты детерминации, коэффициенты эластичности и средние относительные ошибки аппроксимации. Сравнить модели по этим характеристикам и сделать вывод. Решение 1. Уравнение линейной регрессии имеет вид: = а0 + а1x. Построим линейную модель. Для удобства выполнения расчетов предварительно упорядочим всю таблицу исходных данных по возрастанию факторной переменной Х (Данные => Сортировка). ( ...


0 комментариев