Линейный множественный регрессионный анализ

МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ УКРАИНЫ

ХЕРСОНСКИЙ НАЦИОНАЛЬНЫЙ УНЕВЕРСИТЕТ

КАФЕДРА ЭКОНОМИЧЕСКОЙ КИБЕРНЕТИКИ

Реферат

по дисциплине: „Методы анализа данных”

на тему: „Линейный множественный регрессионный анализ”

Выполнил:

Студент гр. 4ЭК2

Приходько Е.А.

Проверил:

Преподаватель

Больова Г.А.

Херсон-2008

Содержание

1.  Регрессионный анализ

2.  Основы линейного регрессионного анализа

3.  Множественная линейная регрессия

4.  Линейный множественный регрессионный анализ

1.  Регрессионный анализ

Если расчёт корреляции характеризует силу связи между двумя переменными, то регрессионный анализ служит для определения вида этой связи и дает возможность для прогнозирования значения одной (зависимой) переменной отталкиваясь от значения другой (независимой) переменной. Для проведения линейного регрессионного анализа зависимая переменная должна иметь интервальную (или порядковую) шкалу. В то же время, бинарная логистическая регрессия выявляет зависимость дихотомической переменной от некой другой переменной, относящейся к любой шкале. Те же условия применения справедливы и для пробит-анализа. Если зависимая переменная является категориальной, но имеет более двух категорий, то здесь подходящим методом будет мультиномиальная логистическая регрессия можно анализировать и нелинейные связи между переменными, которые относятся к интервальной шкале. Для этого предназначен метод нелинейной регрессии.

2. Основы линейного регрессионного анализа

 

Раздел многомерного статистического анализа, посвященный восстановлению зависимостей, называется регрессионным анализом. Термин "линейный регрессионный анализ" используют, когда рассматриваемая функция линейно зависит от оцениваемых параметров (от независимых переменных зависимость может быть произвольной). Теория оценивания неизвестных параметров хорошо развита именно в случае линейного регрессионного анализа. Если же линейности нет и нельзя перейти к линейной задаче, то, как правило, хороших свойств от оценок ожидать не приходится. Продемонстрируем подходы в случае зависимостей различного вида. Если зависимость имеет вид многочлена (полинома)

то коэффициенты многочлена могут быть найдены путем минимизации функции

Функция от t не обязательно должна быть многочленом. Можно, например, добавить периодическую составляющую, соответствующую сезонным колебаниям.

Хорошо известно, например, что инфляция (рост потребительских цен) имеет четко выраженный годовой цикл - в среднем цены быстрее всего растут зимой, в декабре - январе, а медленнее всего (иногда в среднем даже падают) летом, в июле - августе.

Пусть для определенности

тогда неизвестные параметры могут быть найдены путем минимизации функции

Пусть I(t) -индекс инфляции в момент t. Принцип стабильности условий приводит к гипотезе о постоянстве темпов роста средних цен, т.е. индекса инфляции. Таким образом, естественная модель для индекса инфляции – это

Эта модель не является линейной, метод наименьших квадратов непосредственно применять нельзя. Однако если прологарифмировать обе части предыдущего равенства:

то получим линейную зависимость, рассмотренную в первом пункте настоящей главы.

Независимых переменных может быть не одна, а несколько. Пусть, например, по исходным данным требуется оценить неизвестные параметры a и b в зависимости

где  - погрешность. Это можно сделать, минимизировав функцию

Зависимость от х и у не обязательно должна быть линейной. Предположим, что из каких-то соображений известно, что зависимость должна иметь вид

тогда для оценки пяти параметров необходимо минимизировать функцию

Более подробно рассмотрим пример из микроэкономики. В одной из оптимизационных моделей поведения фирмы используется т.н. производственная функция f(K,L), задающая объем выпуска в зависимости от затрат капитала K и труда L. В качестве конкретного вида производственной функции часто используется так называемая функция Кобба-Дугласа

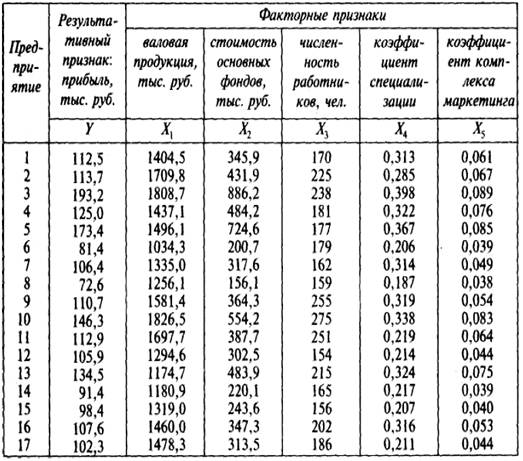
Однако откуда взять значения параметров  и ? Естественно предположить, что они - одни и те же для предприятий отрасли. Поэтому целесообразно собрать информацию где f_k- объем выпуска на k-ом предприятии, K_k- объем затрат капитала на k-ом предприятии, L_k- объем затрат труда на k-ом предприятии (в кратком изложении здесь не пытаемся дать точных определений используемым понятиям из экономики предприятия). По собранной информации естественно попытаться оценить параметры  и . Но они входят в зависимость нелинейно, поэтому сразу применить метод наименьших квадратов нельзя. Помогает логарифмирование:

Следовательно, целесообразно сделать замену переменных

а затем находить оценки параметров  и , минимизируя функцию

Найдем частные производные:

 

Приравняем частные производные к 0, сократим на 2, раскроем скобки, перенесем свободные члены вправо. Получим систему двух линейных уравнений с двумя неизвестными:

Таким образом, для вычисления оценок метода наименьших квадратов необходимо найти пять сумм:

Для упорядочения расчета этих сумм может быть использована таблица типа той, что применялась в первом пункте настоящей главы. Отметим, что рассмотренная там постановка переходит в разбираемую сейчас при

Подходящая замена переменных во многих случаях позволяет перейти к линейной зависимости. Например, если

то замена z=1/y приводит к линейной зависимости z = a + bx. Если y=(a+bx)², то замена  приводит к линейной зависимости z = a + bx.