Навигация
Множественная линейная регрессия
3. Множественная линейная регрессия
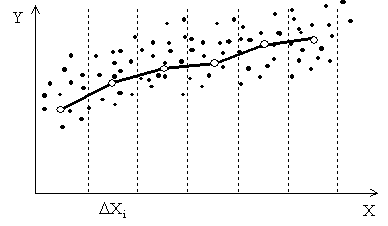
В общем случае в регрессионный анализ вовлекаются несколько независимых переменных. Это, конечно же, наносит ущерб наглядности получаемых результатов, так как подобные множественные связи в конце концов становится невозможно представить графически.
В случае множественного регрессионного анализа речь идёт необходимо оценить коэффициенты уравнения
у = b1-х1+b2-х2+... + bn-хn+а,
где n — количество независимых переменных, обозначенных как х1 и хn, а — некоторая константа.
Переменные, объявленные независимыми, могут сами коррелировать между собой; этот факт необходимо обязательно учитывать при определении коэффициентов уравнения регрессии для того, чтобы избежать ложных корреляций.
4. Линейный множественный регрессионный анализ
В практике часто возникают ситуации, когда функция отзыва (цели) Y зависит не от одного, а от многих факторов. Установление формы связи в таких случаях начинают, как правило с рассмотрения линейной регрессии такого вида:
![]()
В таком случае результаты наблюдений должны быть представлены уравнениями, полученными в каждом из п опытов:
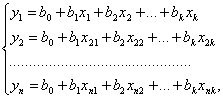 (1)
(1)
или в виде матрицы результатов наблюдений:

где п – количество опытов; k - количество факторов.
Для решения системы уравнений (1) необходимо, чтобы количество опытов было не меньше
k + 1, т.е. п ![]() k + 1.
k + 1.
Заданием множественного регрессионного анализа является построение такого уравнения прямой k-мерном пространстве, отклонение результатов наблюдений ![]() от которой были бы минимальными. Используя для этого метод наименьших квадратов, получаем систему нормальных уравнений:
от которой были бы минимальными. Используя для этого метод наименьших квадратов, получаем систему нормальных уравнений:
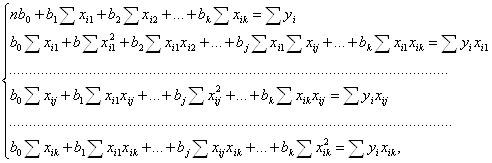
которую представим в матричной форме
(ХТХ)В = XTY, (2)
где В - вектор-столбец коэффициентов уравнения регрессии;
X - матрица значений факторов;
Y - вектор-столбец функции отзыва;
XТ - транспонированная матрица X.
При ![]() = 1,
= 1, ![]() , они соответственно равны:
, они соответственно равны:
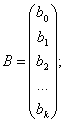
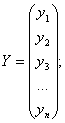


Перемножив правую и левую часть уравнения (2) на обратную матрицу (ХТХ)-1, получим при:
![]()
![]()
![]()
Каждый коэффициент уравнения регрессии вычисляется по формуле:
![]()
где ![]() - элементы обратной матрицы (ХТХ)-1.
- элементы обратной матрицы (ХТХ)-1.
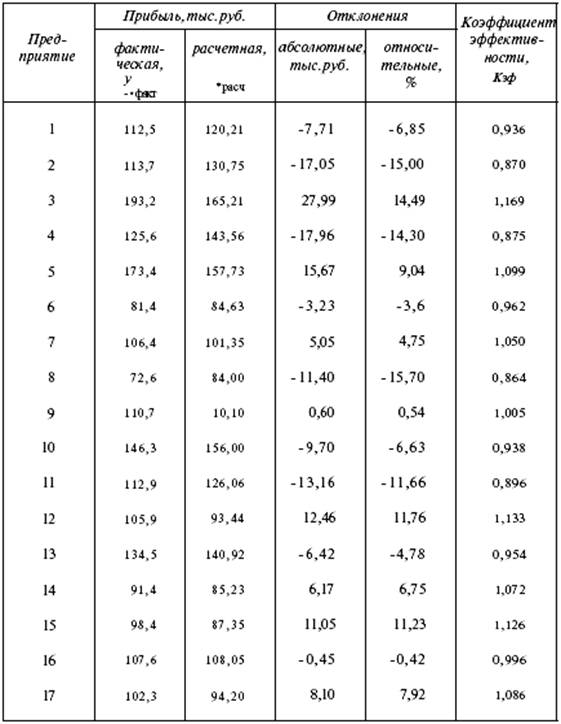
Для проверки значимости уравнения регрессии необходимо при заданных значениях (![]() ) провести несколько экспериментов, чтобы получить некоторое среднее значение функции Y. В этом случае экспериментальный материал представляется, например, в виде табл. 1.
) провести несколько экспериментов, чтобы получить некоторое среднее значение функции Y. В этом случае экспериментальный материал представляется, например, в виде табл. 1.
Таблица 1
| № | Уровни факторов | Значения функции Y при параллельных исследованиях | Исследуемое среднее значение | |||
| x1 | x2 | y1 | y2 | y3 | ||
| 1 | 1,0 | 0,2 | 18,2 | 18,6 | 18,7 | 18,5 |
| 2 | 2,0 | 0,4 | 21,6 | 23,4 | 23,7 | 22,9 |
| 3 | 2,5 | 0,3 | 22,0 | 23,0 | 22,5 | 22,5 |
Число параллельных исследований должно быть больше трёх ![]() .
.
Проверка значимости уравнения регрессии проводится по F-критерию. Для этого вычисляется остаточная дисперсия
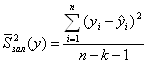
и ![]() -статистика
-статистика
![]()
которая сравнивается с табличным значением ![]() при уровне значимости α и числе ступеней свободы
при уровне значимости α и числе ступеней свободы
k1 = п - 1, k2 = п – k - 1.
Гипотеза про значимость уравнения регрессии принимается при условии:
![]()
Значимость коэффициентов регрессии проверяется по t-критерию.
Статистика 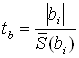 сравнивается с табличным значением
сравнивается с табличным значением ![]() при уровне значимости α и числе степеней свободы
при уровне значимости α и числе степеней свободы
k1 = п – k - 1.
Наклонная коэффициента регрессии:
![]()
где ![]() - диагональный элемент матрицы (ХТХ)-1.
- диагональный элемент матрицы (ХТХ)-1.
Доверительный интервал для коэффициентов регрессии определяется по формуле:
![]()
где В - значение коэффициента регрессии в генеральной совокупности.
Список использованной литературы
1. Александров В.В., Алексеев А.И., Горский Н.Д. Анализ данных на ЭВМ (на примере системы СИТО). – М.: Финансы и статистика, 1990.
2. Блюмин С.Л., Суханов В.Ф., Чеботарев С.В. Экономический факторный анализ: Монография. – Липецк: ЛЭГИ, 2004.
3. Рогальский Ф.Б., Курилович Я.Е., Цокуренко А.А. Математические методы анализа экономических систем. Книга 1. – К.: Наукова думка, 2001.
4. Рогальский Ф.Б., Цокуренко А.А. Математические методы анализа экономических систем. Книга 2. – К.: Наукова думка, 2001.
Похожие работы
... рассматриваемый период можно признать успешной. 3 Парная линейная регрессия Для характеристики влияния изменений Х на вариацию У служат методы регрессионного анализа. В случае парной линейной зависимости строится регрессионная модель Уi = a0 +a1 *Xi + εi, I=1, …,n где n — число наблюдений; a0 ,a1 — неизвестные параметры уравнения; εi, — ошибка случайной переменной У. ...
ТИЧЕСКАЯ ЧАСТЬ 1.1 Теоретические основы прикладного регрессионного анализа Регрессионный анализ применяется для построения математических зависимостей объектов, явлений по результатам экспериментальных данных, полученных на основе проведения активного или пассивного экспериментов. Предполагается, что математическая зависимость относится к определенному классу функций с несколькими ...
... факторами: Параметры данного уравнения найдем с помощью инструмента «Регрессия» надстройки «Анализ данных» приложения MS Excel (результаты вычисления – в Приложении 9): b0= 5,45597214112287 b2= 0,200539077387593 b4= -0,0847616134509301 b5= 0,374792925415136 Получаем уравнение линейной множественной регрессии: Расчетные значения критерия для заданных параметров получили с ...
... можно предположить что при 5% уровне значимости ВАШСП не зависит от инфекции вызывающей реактивный артрит. В связи с тем что не один из показателей активности заболевания а также показатели ВАШ не зависят от инфекции предшествующей реактивному артриту дальнейшее разделение данных на группы можно считать не целесообразным. 2 Множественная линейная регрессия Общее назначение множественной ...

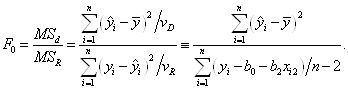

0 комментариев