Построение эмпирической плотности распределения случайной анализируемой величины и расчёт её характеристик
Определение вида закона распределения случайной величины и расчёт его параметров при помощи метода моментов
Определение вида теоретического закона распределения случайной величины графическими методами
Навигация
Построение эмпирической плотности распределения случайной анализируемой величины и расчёт её характеристик
Статистические методы обработки выборочных данных наблюдений или экспериментов
10320
знаков
12
таблиц
10
изображений
2. Построение эмпирической плотности распределения случайной анализируемой величины и расчёт её характеристик
Определяем размах имеющихся данных, т.е. разности между наибольшим и наименьшим выборочным значениями (R = Xmax – Xmin):
Выбор числа интервалов группировки k при числе наблюдений n<100 – ориентировочное значение интервалов можно рассчитать с использованием формулы Хайнхольда и Гаеде:
Тогда ширина интервала:
Результат подсчёта частот и характеристик эмпирического распределения
Таблица 2.
| Границы интервала группировки | Ср.знач. интерв. | Распределение данных | fi | U | U*f | U^2*f |
| 16,4…61,31 | 38,86 | //////////////// | 16 | -1 | -16 | 16 |
| 61,31…106,22 | 83,77 | ////////////////////////// | 26 | 0 | 0 | 0 |
| 106,22…151,13 | 128,68 | //////// | 8 | 1 | 8 | 8 |
| 151,13…196,04 | 173,59 | ////////// | 10 | 2 | 20 | 40 |
| 196,04…240,96 | 218,50 | ///// | 5 | 3 | 15 | 45 |
| 240,96…285,87 | 263,41 | ///// | 5 | 4 | 20 | 80 |
| 285,87…330,78 | 308,32 | //// | 4 | 5 | 20 | 100 |
| 330,78…375,69 | 353,23 | //// | 4 | 6 | 24 | 144 |
| 375,69…420,60 | 398,14 | // | 2 | 7 | 14 | 98 |
| ИТОГО | 80 | 105 | 531 | |||
Принимаем «ложный нуль» x0=83,77 и обозначаем нулем тот интервал, которому соответствует максимальная частота (f=26). Далее, для интервалов, следующих к наименьшему наблюдаемому значению вписываем -1, -2 … и 1, 2, … для интервалов, следующих к наибольшему значению наблюдаемой величины.
Выборочное среднее х и среднеквадратическое отклонение Sx рассчитываем, используя следующие выражения:
(3)
Для построения гистограммы, приведённой на рис.1, по оси абсцисс в выбранном масштабе отмечаем границы интервалов. Левая ось размечается масштабом частот, а на правую, в случае необходимости, можно нанести шкалу относительных частот. На чистом поле гистограммы указываются значения: числа данных; среднего арифметического; среднеквадратического отклонения.
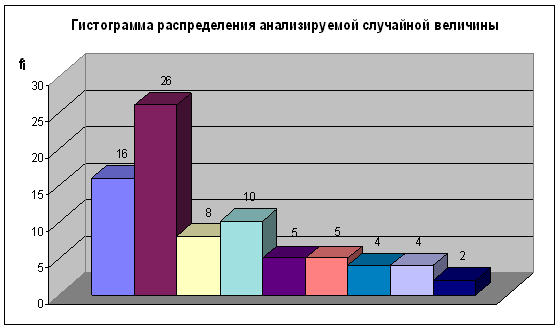
Рис.1
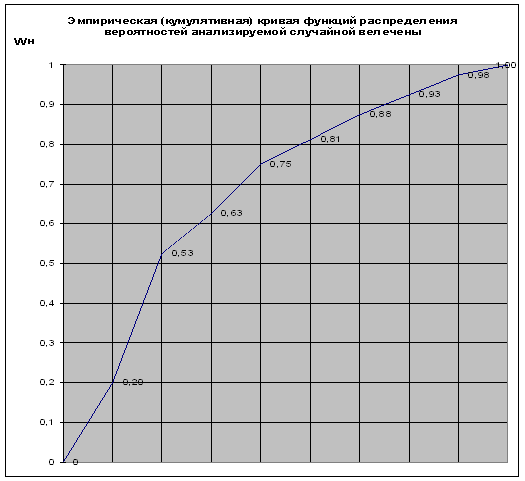
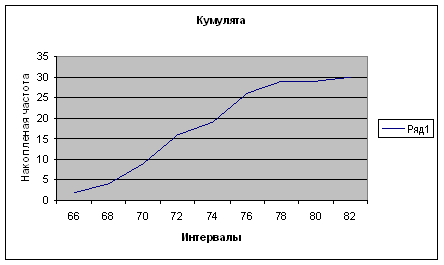
Помимо гистограммы эмпирические данные измерений случайной величины могут быть представлены в виде кумулятивной кривой функции распределения вероятностей. Для этого данные, представленные в табл.1., должны быть дополнены частостями (см. табл.2.).
Частость находим из соотношения:
Таблица частот f и частостей ω.
Таблица 3.
| Границы интервала группировки | Частота,fi | Частость, ω i | Накопленная частость, ω н | |
| 16,4…61,31 | 16 | 0,20 | 0,20 | |
| 61,31…106,22 | 26 | 0,33 | 0,53 | |
| 106,22…151,13 | 8 | 0,10 | 0,63 | |
| 151,13…196,04 | 10 | 0,13 | 0,75 | |
| 196,04…240,96 | 5 | 0,06 | 0,81 | |
| 240,96…285,87 | 5 | 0,06 | 0,88 | |
| 285,87…330,78 | 4 | 0,05 | 0,93 | |
| 330,78…375,69 | 4 | 0,05 | 0,98 | |
| 375,69…420,60 | 2 | 0,03 | 1,00 | |
| ИТОГО | 80 | 1 |
Похожие работы
... если нужно проверить различается ли разброс данных (дисперсии) у двух выборов. Это может использоваться при сравнении точностей обработки деталей на двух станках, равномерности продаж товара в течении некоторого периода в двух городах и т.д. Для проверки статистической гипотезы, о равенстве дисперсий служит F – критерий Фишера. Основной характеристикой критерия является уровень значимости α, ...
... данных, можно достоверно судить о статистических связях, существующих между переменными величинами, которые исследуют в данном эксперименте. Все методы математико-статистического анализа условно делятся на первичные и вторичные. Первичными называют методы, с помощью которых можно получить показатели, непосредственно отражающие результаты производимых в эксперименте измерений. Соответственно под ...
... вывод, что случайная величина распределена по равномерному закону, а случайная величина – по нормальному. Заключение В ходе курсовой работы были освоены методы обработки данных статистического наблюдения, их анализа с помощью обобщающих показателей, установление теоретических законов распределения случайных величин и доказательство адекватности этих законов. Также в результате выполнения ...
Построение неполной квадратичной регрессионной модели по результатам полного факторного эксперимента
... необходимо 24 образца. Неравномерное дублирование предполагает повторение экспериментов в каждой серии опытов неодинаковое число раз. На практике неравномерное дублирование экспериментов используется сравнительно редко из-за сложности построения регрессионных моделей по получаемым опытным данным. При решении прикладных задач материаловедения количество дублей в каждом опыте принимают не менее ...
0 комментариев