Навигация
Определение вида теоретического закона распределения случайной величины графическими методами
4. Определение вида теоретического закона распределения случайной величины графическими методами
Расчёт координат эмпирических точек заданной выборки
Таблица 8.
| № п/п | Среднее значение интервала xi , 103 км | fi , шт | Σ fi | F(x)= Σ fi/n+1 |
| 1 | 38,86 | 16 | 16 | 0,198 |
| 2 | 83,77 | 26 | 42 | 0,519 |
| 3 | 128,68 | 8 | 50 | 0,617 |
| 4 | 173,59 | 10 | 60 | 0,741 |
| 5 | 218,50 | 5 | 65 | 0,802 |
| 6 | 263,41 | 5 | 70 | 0,864 |
| 7 | 308,32 | 4 | 74 | 0,914 |
| 8 | 353,23 | 4 | 78 | 0,963 |
| 9 | 398,14 | 2 | 80 | 0,988 |
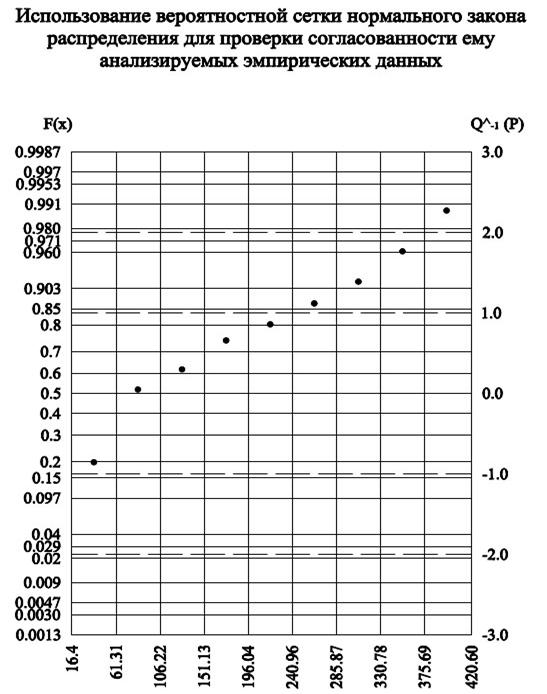
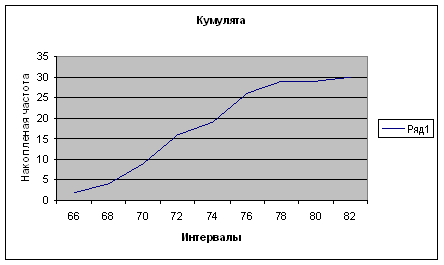
Используя полученные в табл.4. данные, строим вероятностную сетку и выполняем проверку согласованности.
Выбор масштаба построения вероятностной сетки:
· ширина графика (ось абсцисс) А = 140 мм ;
· высота графика (ось ординат) Н = 180 мм .
Нормальный закон распределения
Масштаб значений оси абсцисс устанавливается на основе выражения:
![]()
Таблица 9
| P = F(x) | 0,5 | 0,6 | 0,7 | 0,8 | 0,8413 | 0,85 | 0,903 |
| y = Q-1(P) | 0 | 0,25 | 0,52 | 0,85 | 1 | 1,05 | 1,3 |
| Ky (P), мм | 0 | 7,5 | 15,6 | 25,5 | 30 | 31,5 | 39 |
| P = F(x) | 0,96 | 0,971 | 0,98 | 0,991 | 0,9953 | 0,997 | 0,9987 |
| y = Q-1(P) | 1,75 | 1,9 | 2,05 | 2,35 | 2,6 | 2,75 | 3 |
| Ky(P), мм | 52,5 | 57 | 61,5 | 70,5 | 78 | 82,5 | 90 |
Лгарифмически - нормальный закон распределения
Масштаб значений оси абсцисс устанавливается на основе выражения:
![]()
Таблица 10
| № | Границы интервала | xi 103 км |
|
|
| 1 | 418,78…475,69 | 38,86 | 456,01 | 0,198 |
| 2 | 475,69…499,40 | 83,77 | 489,15 | 0,519 |
| 3 | 499,40…514,62 | 128,68 | 507,68 | 0,617 |
| 4 | 514,62…525,85 | 173,59 | 520,60 | 0,741 |
| 5 | 525,85…534,75 | 218,50 | 530,52 | 0,802 |
| 6 | 534,75…542,12 | 263,41 | 538,59 | 0,864 |
| 7 | 542,12…548,42 | 308,32 | 545,38 | 0,914 |
| 8 | 548,42…553,91 | 353,23 | 551,25 | 0,963 |
| 9 | 553,91…558,78 | 398,14 | 556,42 | 0,988 |
![]()
![]()

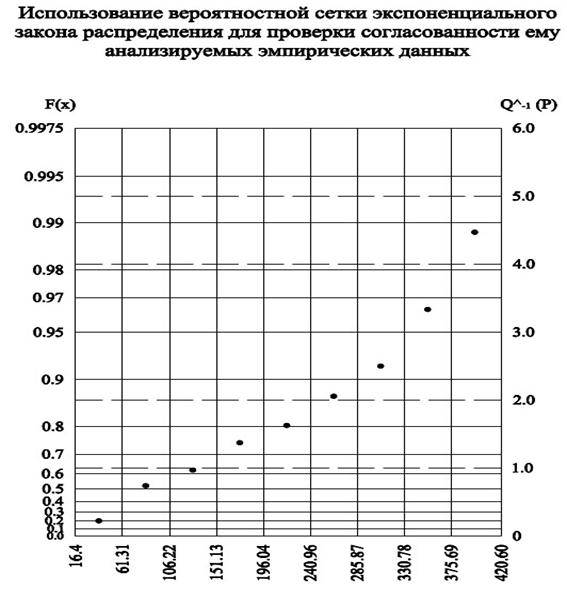
Экспоненциальный (нормальный) закон распределения
Таблица 11
| P = F(x) | 0 | 0,1 | 0,2 | 0,3 | 0,4 | 0,5 | 0,6 | 0,7 |
| Ky (P), мм | 0,0 | 3,2 | 6,7 | 10,7 | 15,3 | 20,8 | 27,5 | 36,1 |
| P = F(x) | 0,8 | 0,9 | 0,95 | 0,97 | 0,98 | 0,99 | 0,995 | 0,9975 |
| Ky(P), мм | 48,3 | 69,1 | 89,9 | 105,2 | 117,4 | 138,2 | 158,9 | 179,7 |
Распределение Вейбулла – Гнеденко
Таблица 12
| P = F(x) | 0,03 | 0,04 | 0,06 | 0,1 | 0,2 | 0,3 | 0,4 |
| y = Q-1(P) | -3,5 | -3,2 | -2,8 | -2,25 | -1,5 | -1,03 | -0,7 |
| Ky (P), мм | -118,8 | -108,6 | -95,0 | -76,4 | -50,9 | -35,0 | -23,8 |
| P = F(x) | 0,5 | 0,632 | 0,78 | 0,9 | 0,97 | 0,955 | 0,999 |
| y = Q-1(P) | -0,36 | 0,00 | 0,41 | 0,83 | 1,25 | 1,66 | 1,93 |
| Ky(P), мм | -12,2 | 0,00 | 13,9 | 28,2 | 42,4 | 56,3 | 65,5 |

Похожие работы
... если нужно проверить различается ли разброс данных (дисперсии) у двух выборов. Это может использоваться при сравнении точностей обработки деталей на двух станках, равномерности продаж товара в течении некоторого периода в двух городах и т.д. Для проверки статистической гипотезы, о равенстве дисперсий служит F – критерий Фишера. Основной характеристикой критерия является уровень значимости α, ...
... данных, можно достоверно судить о статистических связях, существующих между переменными величинами, которые исследуют в данном эксперименте. Все методы математико-статистического анализа условно делятся на первичные и вторичные. Первичными называют методы, с помощью которых можно получить показатели, непосредственно отражающие результаты производимых в эксперименте измерений. Соответственно под ...
... вывод, что случайная величина распределена по равномерному закону, а случайная величина – по нормальному. Заключение В ходе курсовой работы были освоены методы обработки данных статистического наблюдения, их анализа с помощью обобщающих показателей, установление теоретических законов распределения случайных величин и доказательство адекватности этих законов. Также в результате выполнения ...
... необходимо 24 образца. Неравномерное дублирование предполагает повторение экспериментов в каждой серии опытов неодинаковое число раз. На практике неравномерное дублирование экспериментов используется сравнительно редко из-за сложности построения регрессионных моделей по получаемым опытным данным. При решении прикладных задач материаловедения количество дублей в каждом опыте принимают не менее ...
0 комментариев